Alegbra 2- OnRamps Unit 1 and 2

Thinking like a mathematician and Transformations of functions

Set

well-defined collection of elements

S

finite set

ex. {0,1,2,3,4}

P

infinite set

ex. {1, 2, 3…..}

E

empty set

ex. Ø

N

The natural numbers

{1, 2, 3…….}

Z

The integers

{-3, -2, -1, 0, 1, 2, 3}

Q

The set of all rational numbers

ex. a/b

Q^c

The set of all Irrational Numbers

R

The set of real numbers

C

The set of all complex numbers

ex. i= √-1

∈

an element of or belongs to

∃

there exists

∀

for all or for every

: or |

such that

—>

an implication or mapping

Rational Numbers

0, -0.06, 0.75, 0.77777, 36, -49

Irrational Numbers

square roots that can not be simplified into an integer, negative square roots, pi

Closure Axiom

x + y ∈ R

x ⋅ y ∈ R

Commutative Rule Axiom

x+y = y+x

x ⋅ y = y ⋅ x

Associative Rule Axiom

(x+y) +z = (z+y) + x

(xy)z = x(yz)

Identify Elements Axiom

x+0 = x

x⋅1 = x

Inverse Rules Axiom

x+(-x)= 0

x⋅1/x = 1, for x does not equal 0

Distributive Rule

x(y+z)= xy+xz

If an equation/data is a function then:

each input (x) will have only one output

(a single output can have two inputs but a single input can not have two outputs)

A graph is increasing when:

the y values are increasing while the x values are increasing

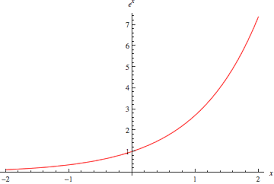
What parent function is this?

y=e^x

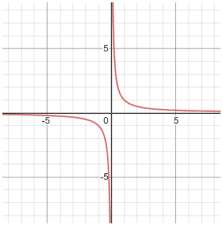
What parent function is this?

f(x)=1/x

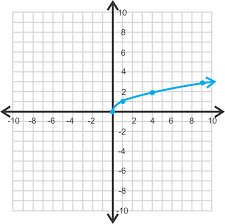
What parent function is this?

f(x)= √x

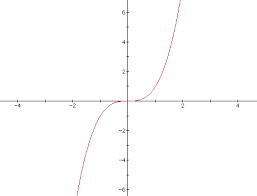
What parent function is this?

f(x)= x³

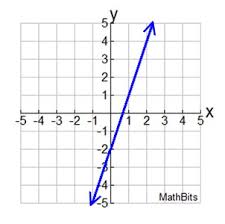
What parent function is this?

f(x)=x

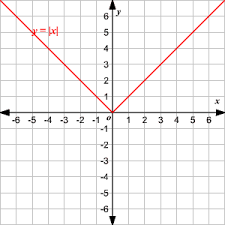
What parent function is this?

f(x)= |x|

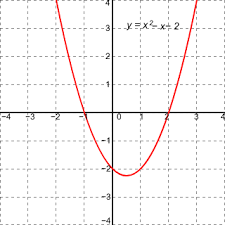
What parent function is this?

f(x)=x²

Slope Intercept Form

y=mx+b

Point-Slope Form

y-y1= m(x-x1)

Standard Form

Ax+By=C

Perpendicular Lines

Lines are perpendicular if one slope is the negative reciprocal of the other

Parallel Lines

Slopes are equal

Vertex of Absolute Value Function Equation

a |x-h|+k

Find x in the absolute value and plug in the x to find y

ex. y=|x-2|+3

x-2

x=2

|2-2|+3= 3

(2,3) Vertex

Horizontal Shift Right

g(x)= f(x-k)

Horizontal Shift left

g(x)= f(x+k)

Vertical Shift

Up: g(x)= f(x)+k

Down: g(x)= f(x)-k

Reflection about the y-axis

g(x)= f(-x)

Reflection about the x-axis

g(x)=-f(x)

Vertical Stretch/compression

g(x)=kf(x)

If K is greater than 1 then the graph will be stretched

If K is less than 1 but greater than 0 then the graph will be compressed

If K is less than 0 then it will be a combination of a vertical stretch/compression and a vertical reflection