10 Slope of a Curve, Velocity, and Rates of Change

Main Objective for Solving for Rates of Change and Tangent Lines

(1) we are using limits to find the slope of the tangent line to a curve at a point

Slope of a Curve at a Point

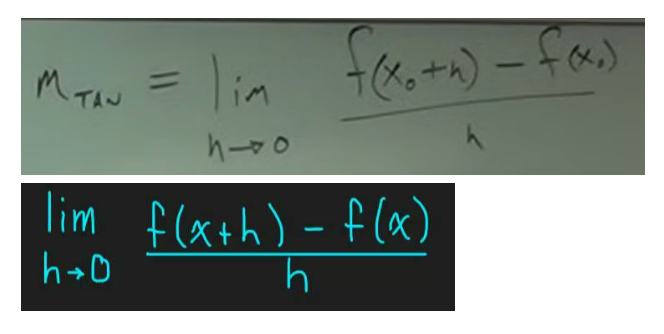
Steps to Finding the Equation of A Tangent Line When Given: (1) Function, (2) Point, (3) Tangent Line Formula

Given: (1) Function, (2) Point

A. Slope — Limits

• Step 1: Identify and write function in function notation — given function

• Step 2: With the given point, identify X₀

• Step 3: With X₀, identify f (X₀ + h) and f (X₀); leave the h alone, these are your inputs

• Step 4: Use these inputs f (X₀ + h) and f (X₀) to plug into your given function to find the outputs of f (X₀ + h) and f (X₀)

• Step 5: Use the outputs to plug into slope of a tangent formula

• Step 6: Solve for the slope of a tangent but solving for the limit.

  • 1) Plug and solve

  • 2) Factor, simplify, plug and solve

  • 3) Rationalize, simplify, plug and solve

  • Cross and simplify h in the denominator

B. Point-Slope Formula — Equation of a Line

• Step 7: Solve for the equation of a line now with the slope of a tangent and the given point, by plugging in the point and the slope into the point-slope formula, and simplify

Point-Slope Formula

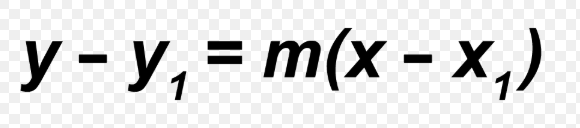
Does every single point of a curve have the same slope?

No. Every single point of that curve has a different tangent line, therefore a different slope every time.

Steps to Finding the General Slope of A Tangent Line (At Any Point) When Given: (1) Function,  (2) Formula

Given: (1) Function, (2) Point

A. Slope — Limits

• Step 1: Identify and write function in function notation — given function

• Step 2: With the given point, identify X₀

• Step 3: With X₀, identify f (X₀ + h) and f (X₀); leave the h alone, these are your inputs

• Step 4: Use these inputs f (X₀ + h) and f (X₀) to plug into your given function to find the outputs of f (X₀ + h) and f (X₀)

• Step 5: Use the outputs to plug into slope of a tangent formula

• Step 6: Solve for the slope of a tangent but solving for the limit.

  • 1) Plug and solve

  • 2) Factor, simplify, plug and solve

  • 3) Rationalize, simplify, plug and solve

  • Cross and simplify h in the denominator

Average Velocity Formula

Steps to Finding Average Velocity

Step 1: Identify and write function in function notation

Step 2: Find starting time or starting position, T₀

Step 3: With T₀, identify f (T₀ + h) and f (T₀), leave h alone, these are your inputs

Step 4: Plug inputs to get outputs

Step 5: Use outputs to plug into average velocity formula

Step 6: Solve for the slope, you will get a constant

Instantaneous Velocity Formula

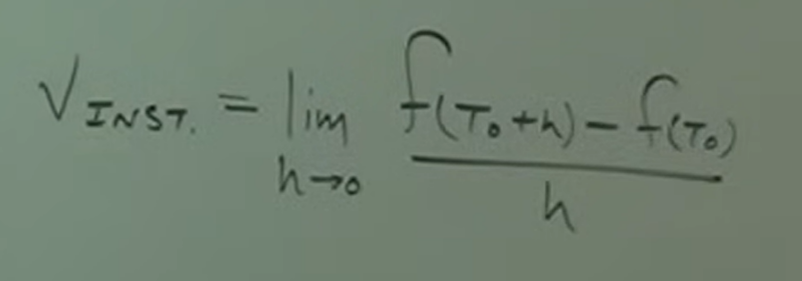
Steps to Finding Instantaneous Velocity

Step 1: Identify the function, write in function notation

Step 2: Identify your time at that instant, T₀

Step 3: With T₀, identify f (T₀ + h) and f (T₀), leave h alone, these are your inputs

Step 4: Plug inputs to get outputs

Step 5: Use outputs to plug into instantaneous velocity formula

Step 6: Solve for the slope using limits

• 1) Plug and solve

• 2) Factor, simplify, plug and solve

• 3) Rationalize, simplify, plug and solve

• Cross and simplify h in the denominator

• Negatives are acceptable since they’re vector units

Steps to Finding Instantaneous Velocity at Any Time (General Slope of a Curve)

• Step 1: Identify and write function in function notation — given function

• Step 2: With the given point, identify T₀

• Step 3: With X₀, identify f (T₀ + h) and f (T₀); leave the h alone, these are your inputs

• Step 4: Use these inputs f (X₀ + h) and f (X₀) to plug into your given function to find the outputs of f (T₀ + h) and f (T₀)

• Step 5: Use the outputs to plug into slope of a tangent formula

• Step 6: Solve for the slope of a tangent but solving for the limit.

  • 1) Plug and solve

  • 2) Factor, simplify, plug and solve

  • 3) Rationalize, simplify, plug and solve

  • Cross and simplify h in the denominator

Average Rate of Change Formula

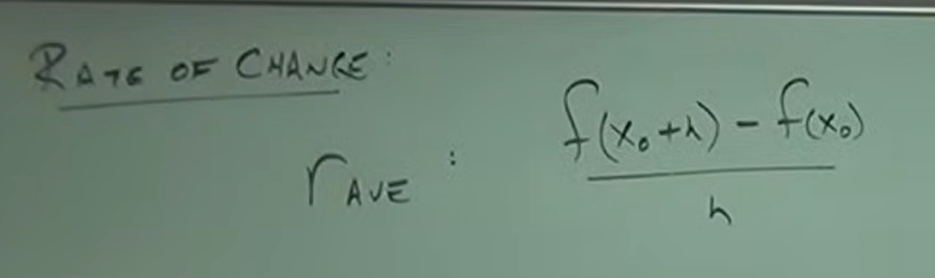
Steps to Finding Average Rate of Change

Step 1: Identify and write function in function notation

Step 2: Find starting time or starting position, X₀

Step 3: With X₀, identify f (X₀ + h) and f (X₀), leave h alone, these are your inputs

Step 4: Plug inputs to get outputs

Step 5: Use outputs to plug into average rate of change formula

Step 6: Solve for the slope, you will get a constant

Instantaneous Rate of Change Formula

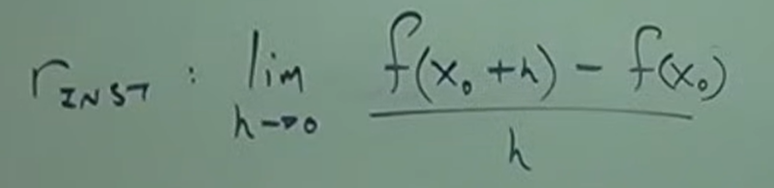
Steps to Finding Instantaneous Rate of Change

Step 1: Identify the function, write in function notation

Step 2: Identify your time at that instant, X₀

Step 3: With X₀, identify f (X₀ + h) and f (X₀), leave h alone, these are your inputs

Step 4: Plug inputs to get outputs

Step 5: Use outputs to plug into instantaneous velocity formula

Step 6: Solve for the slope using limits

• 1) Plug and solve

• 2) Factor, simplify, plug and solve

• 3) Rationalize, simplify, plug and solve

• Cross and simplify h in the denominator