Chapter 5 Geometry Test theorems

Defn of a Trapezoid and its bases and legs

A quadrilateral with exactly one pair of parallel sides. The parallel sides are called bases and the other sides are the legs.

Defn of an Isosceles Trapezoid

A trapezoid with congruent legs

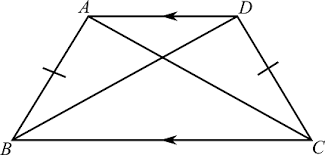
What theorem has to do with the bases of this isosceles trapezoid?

Base angles of an isosceles trapezoid are congruent

The median of a trapezoid

The segment that joins the midpoints of the legs of a trapezoid

The median of a triangle

The line segment from a vertex to the midpoint of the opposite side

The altitude of a triangle

The perpendicular segment from a vertex to a line that contains the opposite side

The perpendicular bisector of a triangle

A line, segment, or ray that is perpendicular to a segment and its midpoint

Properties of the median of a trapezoid are:

1. Parallel to the bases

2. Have the length equal to the average of the base lengths

Defn of a parallelogram

A quadrilateral with both pairs of opposite sides parallel

Properties of a parallelogram

1. Opposite sides of a parallelogram are congruent

2. Opposite angles of a parallelogram are congruent

3. Diagonals of a parallelogram bisect each other

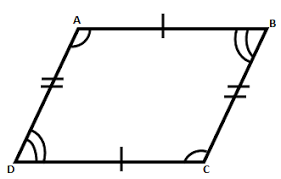
How would you prove that this is a parallelogram

If both pairs of opposite sides of a quadrilateral are congruent then the quadrilateral is a parallelogram.

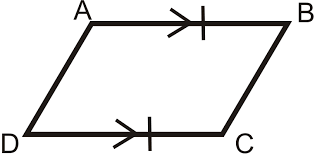
How would you prove that this is a parallelogram

If one pair of opposite sides of a quadrilateral are both congruent and parallel then the quadrilateral is a parallelogram

How would you prove that this is a parallelogram

If both pairs of opposite angles of a quadrilateral are congruent then the quadrilateral is a parallelogram

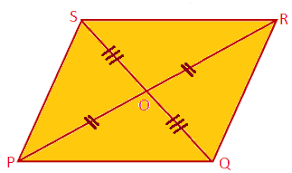
How would you prove that this is a parallelogram

If the diagonals of a quadrilateral bisect each other then the quadrilateral is a parallelogram

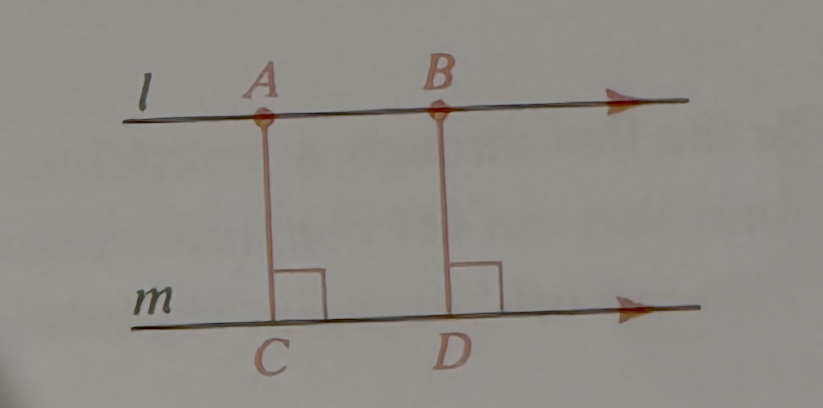
What can you conclude from this diagram about the two points on the parallel lines?

If two lines are parallel then all points on one line are equidistant from the other line

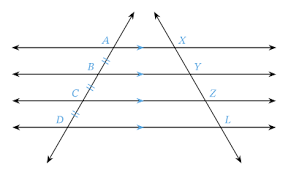
What can you conclude from this diagram about the transversal?

If three parallel lines cut off congruent segments on one transversal then they cut off congruent segments on every transversal

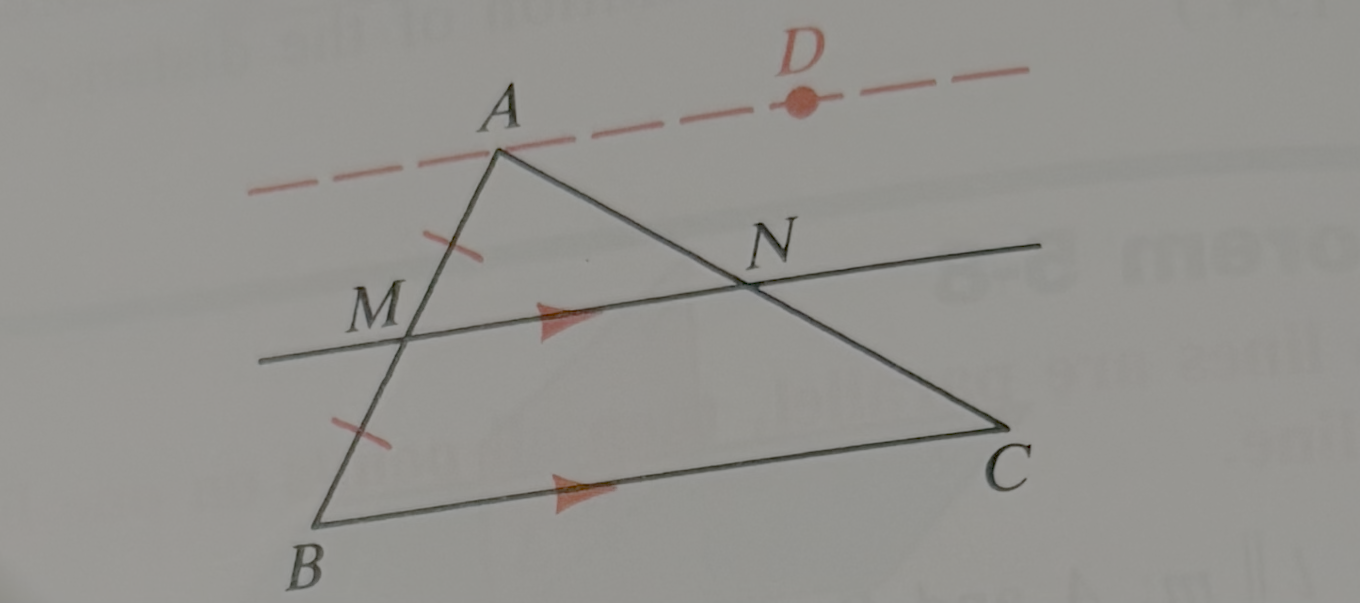
What can you conclude about point N (hint it has to do with a midpoint)

A line that contains the midpoint of one side of a triangle is parallel to another side passes through the midpoint of the third side

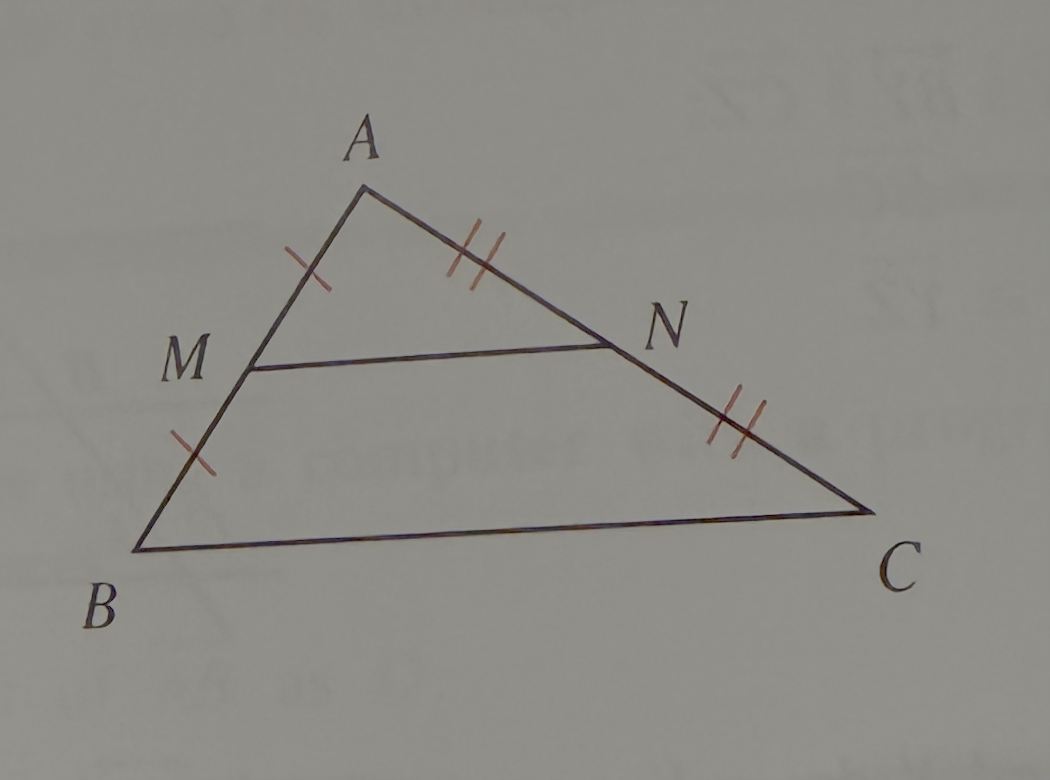
The segment that joins the midpoint of two sides of a triangle are:

1. Parallel to the third side

2. Half as long as the third side

Defn of a rectangle

a quadrilateral with four right angles

Defn of a rhombus

a quadrilateral with four congruent sides

Defn of a square

a quadrilateral with four right angles and four congruent sides

Extra property of a rectangle aside from it being a parallelogram

The diagonals of a rectangle are congruent

Extra properties of a rhombus aside from it being a parallelogram

1. The diagonals of a rhombus are perpendicular to each other

2. Each diagonal of a rhombus bisect two angles of the rhombus

Extra properties of a square aside from it being a parallelogram

1. a square is a rectangle

2. A square is a rhombus

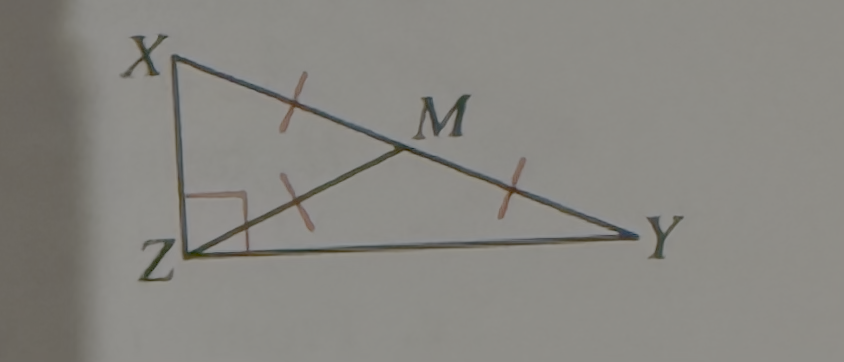
What can you conclude about point M

The midpoint of the hypotenuse of a right triangle is equidistant from the three vertices

How can you conclude if a parallelogram is a rectangle?

If an angle of a parallelogram is a right angle then the parallelogram is a rectangle

How can you conclude if a parallelogram is a rhombus

If two consecutive sides of a parallelogram are congruent then the parallelogram is a rhombus

What happens when the transversal of 2 parallel lines are perpendicular to one of the two parallel lines?

If the transversal is perpendicular to one of two parallel lines then it is perpendicular to the other also

How to say that the angles of an isosceles triangle are congruent

If two sides of a triangle are congruent then the angles opposite those sides are congruent.

What is true about the bisector of a vertex angle of an isosceles triangle

The bisector of the vertex angle of an isosceles triangle is perpendicular to the base at its midpoint

What is true about a point on the perpendicular bisector of a segment? What is the inverse

1. If a point lies on the perpendicular bisector of a segment then the point is equidistant from the endpoints of the segment

2. If a point is equidistant from the endpoints of a segment then the point lies on the perpendicular bisector of the segment

What is true about a point on the bisector of an angle? What is the inverse

1. If a point lies on the bisector of an angle then the point is equidistant from the sides of the angle

2. If a point is equidistant from the sides of an angle then the point lies on the bisector of the angle