AP pre-calculus review

a_n=a_k+d(n-k) or a _n=a₀+dn

Arithmetic sequences

g_n=g₀(r)^n or g_n=g_k(r)^(n-k)

Geometric sequence

r=a_n/a_n-1

Common ratio

a(b)^(x-1)+k

Exponential

log_b(MN)=log_bM+log_bN

Product property

Log_b(M/N)=log_bM-log_bN

Quotient Property

Log_bN^p=p(log_bN)

Power Property

y=sinx

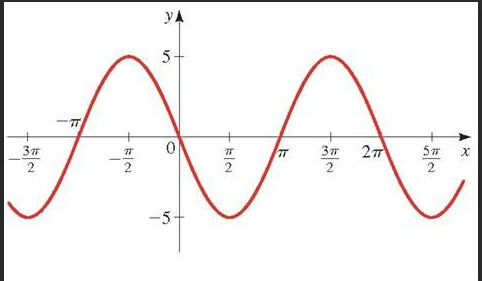
y=cosx

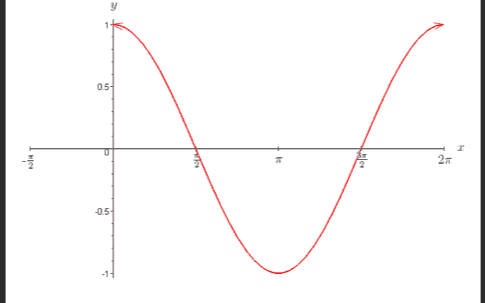
y=tanx

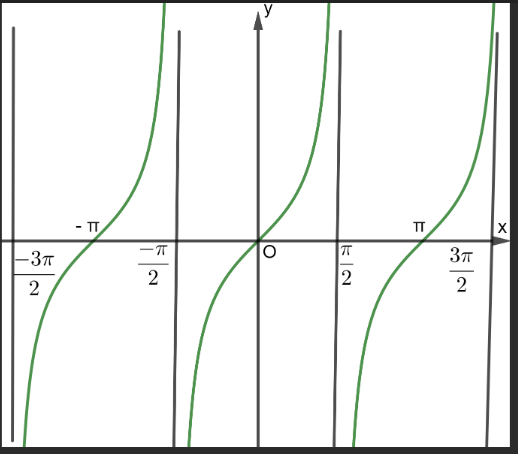
y=cscx

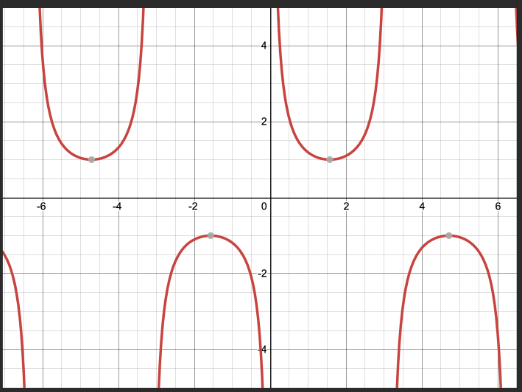
y=secx

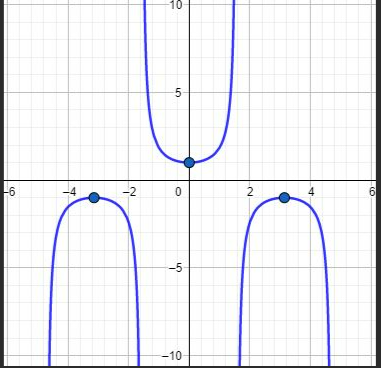
y=cotx

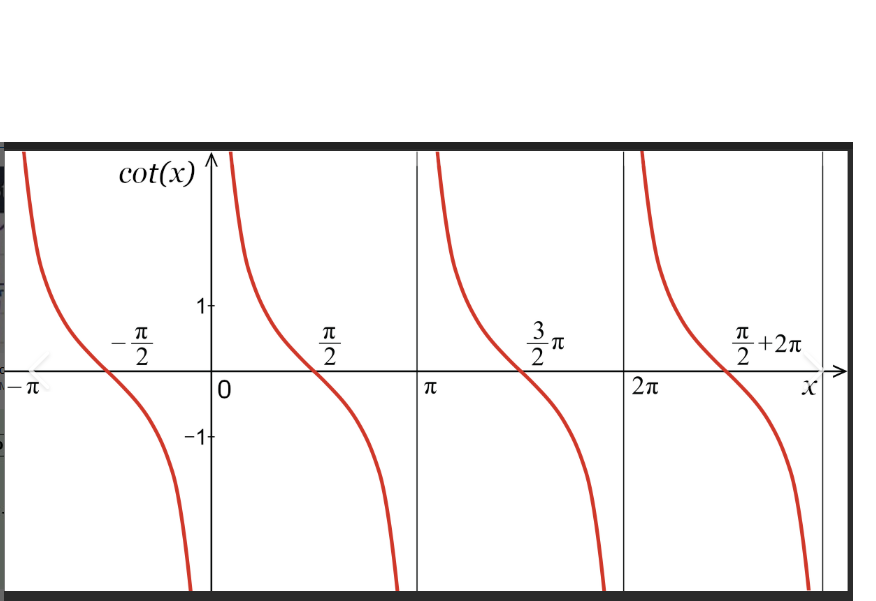
sin²x+cos²x=1

1+tan²x=sec²x

cot²x+1=csc²x

Pythagorean Theorom

2sinxcosx

sin(2x)=

cos^2x-sin^2x

2cos^2x-1

1-2sin^2x

cos(2x)=

sinAcosB+cosAsinB

sin(A+B)=

cosAcosB-sinAsinB

cos(A+B)=

sinAcosB-cosAsinB

sin(A-B)=

cosAcosB+sinAsinB

cos(A-B)=

The amplitude, A=(max-min)/2

y=Asin[B(x+c)]+D, y=Acos[B(x+c)]+D

A is…

Number cycles in 2π

y=Asin[B(x+c)]+D, y=Acos[B(x+c)]+D

B is…

(2π)/B

Period

B/(2π)

Frequency

Phase shift

y=Asin[B(x+c)]+D, y=Acos[B(x+c)]+D

C is…

Midline (y=D)

D=(max+min)/2

y=Asin[B(x+c)]+D, y=Acos[B(x+c)]+D

D is…

The location for points of inflection on tangent curve

y=Atan[B(x+C)]+D

D is…

Phase shift

y=Atan[B(x+C)]+D

C is…

Period=π/B

y=Atan[B(x+C)]+D

B is…

x=(π/2)+kπ

y=Atan[B(x+C)]+D

Vertical asymptotes

x=rcosθ

X value in a polar coordinate is…

y=rsinθ

Y value in a polar coordinate is…

Distance from the origin is increasing

When r=f(θ) is increasing, and r is positive…

Distance from the origin is decreasing

When r=f(θ) is decreasing, and r is positive

Distance from the origin is decreasing

When r=f(θ) is increasing and r is negative

the distant from the origin is increasing.

When r=f(θ) is decreasing and r is negative

r(θ)=θ

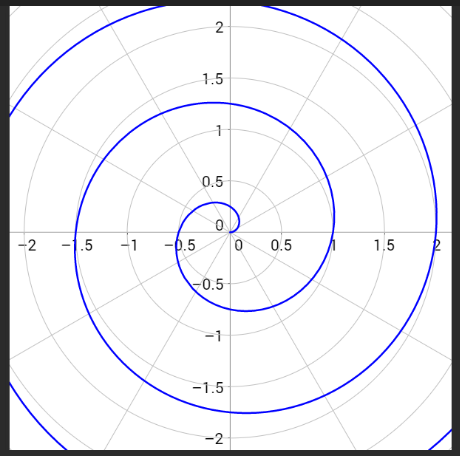
r=acosθ

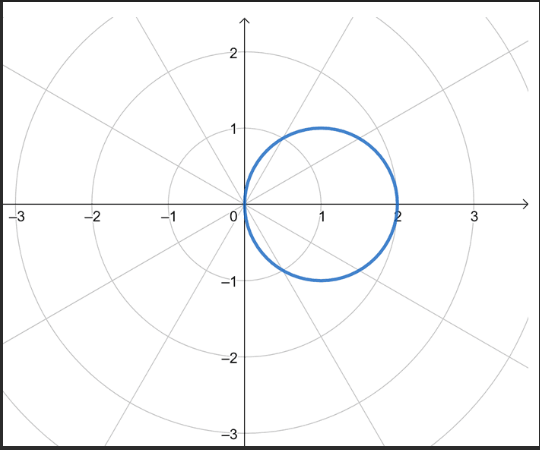
r=asinθ

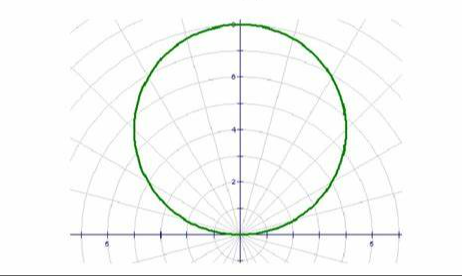
r= a+-bcosθ (a/b =1) Cardioids

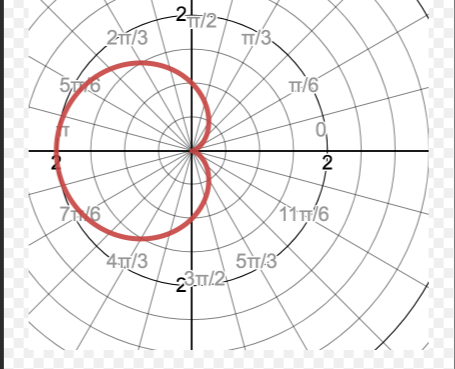
r= a+-bsinθ (a/b =1) Cardioids

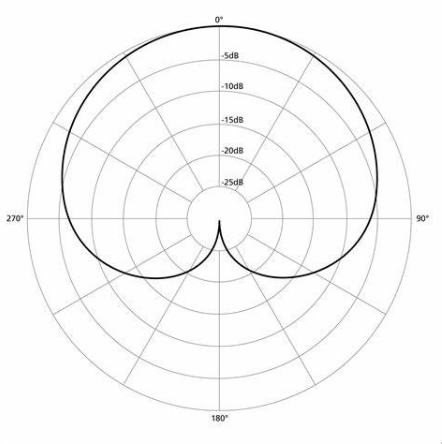
r= a+-bcosθ (a/b >2) Convex Limacon

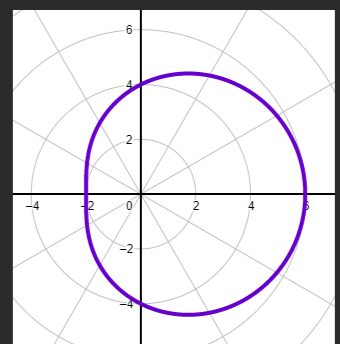
r= a+-bsinθ (a/b >2) Convex Limacon

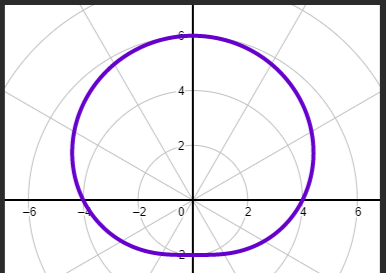
r= a+-bcosθ (a/b <1) Limacon

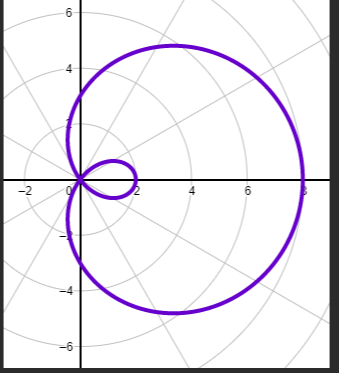
r= a+-bsinθ (a/b <1) Limacon

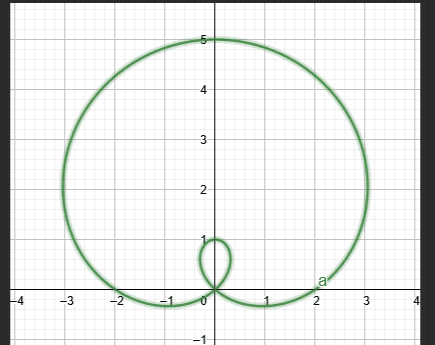
r= acos(nθ)

n=3,odd

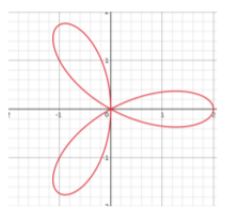
r= asin(nθ)

n=4,even