Further Mech - Impulse and Momentum (Physics Model Answers)

1. Define Impulse

Change in momentum.

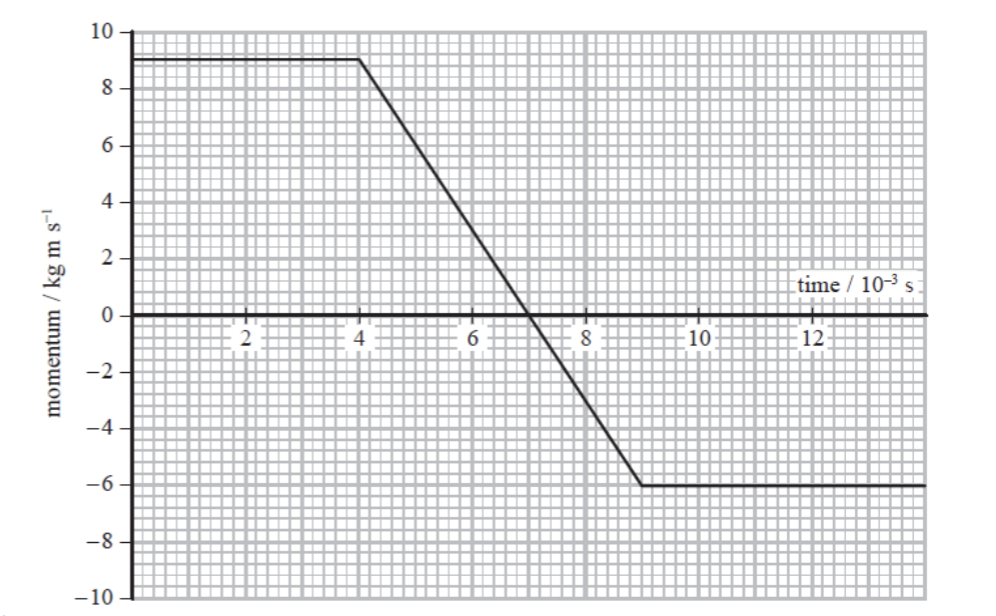
2. A momentum tie graph is shown for a ball impacting with a wall. Calculate the force exerted on the ball, by the wall.

• Force = change in momentum / time

• -6 - 9 / 5 × 10^-3

• 15 / 5 × 10^-3

• 3000 N

3. State the principle of conservation of momentum.

• The total momentum before and after a collision is always the same.

• Provided no external forces act.

4. Applying Newton’s 2nd and 3rd laws of motion, to the collision between two pucks leads to the conclusion that momentum is conserved. Justify this statement.

• Applying Newton’s 3rd Law, when one puck A exerts a force on the other puck B, puck B exerts an equal and opposite force on puck A. We can write this F_A = - F_B.

• Due to Newton’s 2nd Law, F = Δp/Δt . So Δp_A / Δt_A = -Δp_B / Δt_{B .}

• The forces act for the same time, Δt_A = Δt_B .

• So Δp_A = - Δp_B

• Therefore Δp_A + Δp_B = 0. ie. the total change in momentum is zero, so momentum is conserved.

5. Define inelastic collision.

• A collision where the total kinetic energy after the collision is less than the total kinetic energy before the collision.

6. Describe some examples of inelastic collsions.

• When objects stick together, this must be an inelastic collision.

• If an object changes shape, work will have been done to change the shape of the obejct, so kinetic energy will be transferred into the internal energy store of the material and this will be an inelastic collision.

7. Define elastic collision.

A collision where the total kinetic energy before and after a collision is the same.

8. A piece of plasticine is fired from a spring gun. It travels through the air and hits a wooden pendulum bob and sticks to it. The bob and clay move up to a maximum height. Describe how the principle of energy conservation and the principle of momentum conservation apply to this situation.

• The spring stores elastic potential energy which is transferred into kinetic energy of the clay.

• During the collision, the clay deforms and sticks to the bob, so this is an inelastic collision and kinetic energy is not conserved - work is done to change the shape of the clay, increasing its internal energy (thermal energy).

• The bob and clay have kinetic energy as they move together, and this kinetic energy is transferred into GPE, until at maximum height all the KE has become GPE.

• Momentum conservation applies during the collision.

• The momentum of the clay before the collision is equal to the momentum of the clay + bob after the collision. The speed of the combined clay + bob, must be less than that of the clay alone.

9. The identical spheres of mass m are both travelling with a speed v towards each other. What is true after the collision?

B - The total momentum after the collision must be zero. Each ball has an equal momentum but in the opposite direction so the total is mv - mv = 0 kgm/s. The total kinetic energy could be mv² if the balls move away from each other at the same speed that they initially collided with (elastic), or it could be 0 if the balls stick together and are stationary (inelastic).

*In both cases total momentum would still be zero. Total KE after collision could also range drom 0 to mv² as long as each ball has the same speed in opposite directions.

10. Whilst moving, empty fuel tanks can be ejected by means of an explosion. This has the effect of increasing the speed of the probe. Discuess whether conservation of momentum and conservation of energy apply in this situation and why the speed of the probe increases.

• Conservation of momentum does apply.

• The probe and tank experience equal and opposite changes in momentum.

• They change their speed in opposite directions.

• Total energy is conserved.

• But the kinetic energy of the system increases.

• This means chemical energy must have been converted into kinetic energy.

11. A moving ball A, collides with an identical stationary ball B, on ice. It makes a direct hit and the collision is elastic. Just before the collision, ball A has a velocity, v. After the collision, ball B has a velocity, v. Discuss how the relavent conservation laws apply to this collision. [6]

• The collision takes place on ice, so there is minimal friction - external forces are negligible.

• So momentum is conserved.

• The momentum of ball A before the collision equals the momentum of ball A+B after the collision.

• As B has the same momentum as A did before, ball A must be at reast after the collision.

• All of the kinetic energy of ball A must be transferred to ball B.

• As kinetic energy is conserved in an elastic collision.

12. Derive the expression for KE in terms of momentum.

• p = mv

• v = p/m

• KE = ½ mv²

• KE = ½ m (p/m)²

• KE = p² / 2m