AP Calculus AB Review

lim f(x)

x→c

limit notation

limit

The value that f(x) approaches as x approaches c from the left and right sides.

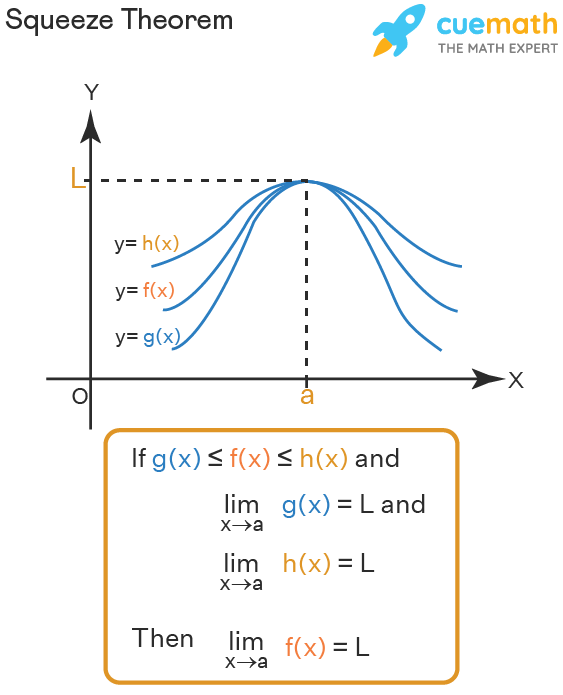
Squeeze Theorem

h(x) ≤ f(x) ≤ g(x) for all x in an open interval containing c, and lim x → c h(x) =L = lim x→ c g(x), then lim x → c f(x)= L

lim f(x) = 0
x → infinity

degree of numerator < degree of denominator (horizontal asymptote)

lim f(x) = leading coefficient of numerator / leading coefficient of denominator

x → infinity

If the degrees of the numerator and denominator are equal. (horizontal asymptote)

f(x) → positive or negative infinity

degree of denominator > degree of numerator

f(x) is continuous @ x=c if

• f(c) exists → no holes/asymptote

• the limit f(x) exists

• f(c) = limit f(x) as x → c

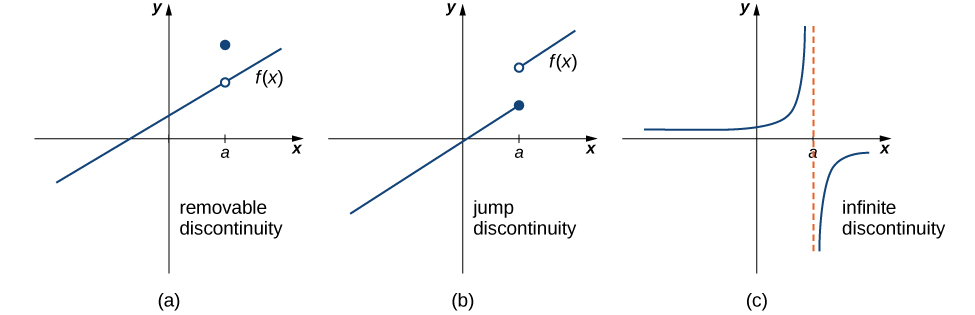
removable discontinuity (hole)

f(c) ≠ limit f(x) as x → c

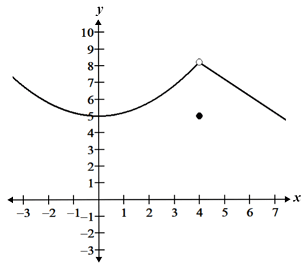
non removable discontinuity

• vertical asymptote: f(c) ≠ exist

• jump: limit f(x) as x → c ≠ exist

Intermediate value theorem

If f is continuous on [a,b], then f(x) takes any value between f(a) and f(b).

derivative (instantaneous rate of change)

The slope of the tangent line to a function at a point.

Instantaneous rate of change (c+h)

limit as h → 0 f(c+h) - f(c) over h

Instantaneous rate of change (c and x)

limit as x → c f(x) - f(c) over x - c

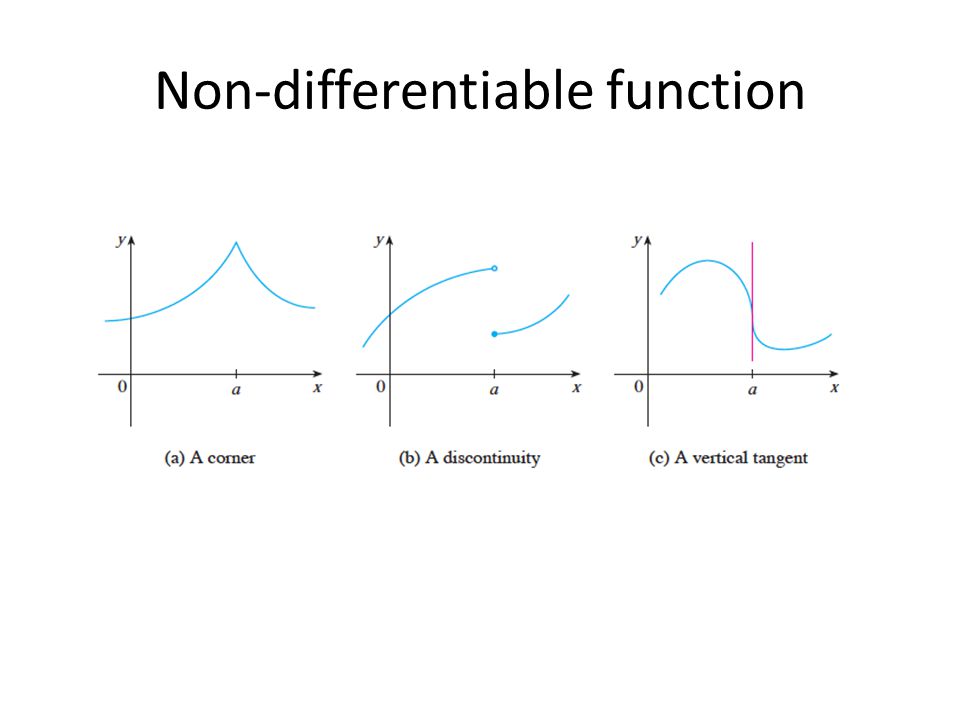
f(x) is not continuous when

• hole

• asymptote

• jump

• sharp turn

• cusp

• vertical tangent line on a function

d/dx c

0

d/dx cf(x)=

c * d/dx f(x)

d/dx (f(x)+-g(x))=

d/dx f(x) +- d/dx g(x)

d/dx x^n=

nx^n-1

d/dx e^x=

e^x

d/dx lnx=

1/x

d/dx sinx =

cosx

d/dx cosx =

-sinx

d/dx tanx =

sec²x

d/dx cotx =

-csc²x

d/dx secx =

secxtanx

d/dx cscx =

-cscxcotx

product rule

fs’+sf’

quotient rule

lodhi-hidlo over lo²

Chain Rule

y’ = f’(g(x) * g’(x)

Implicit Differentiation

1. Differentiate both sides with/ respect to X

2. Collect all terms w/ dy/dx to one side and all terms w/o dy/dx to the other side.

3. Factor out dy/dx

4. Solve dy/dx by dividing

Derivative of an inverse function

(f^-1)’(b) = 1/f(‘x) (slope at inverse points are reciprocals)

d/dx(arcsin u)

u’/sqrt (1-u²)

d/dx (arccos u)

u’/-sqrt (1-u²)

d/dx (arctan u)

u’/1+u²

position s(t)

Positive is to the right /above the origin

Negative is left/below the origin

velocity v(t)

• v(t) > 0 object is moving right/up

• v(t) < 0 object is moving left/down

• v(t) = 0 object is at rest

• v(t) = s’(t)

constant velocity

means acceleration is not changing, a=0

acceleration

a(t) = v’(t) = s“(t)

speeding up

a(t) and v(t) have the same signs

slowing down

a(t) and v(t) have opposite signs

related rates

1. Draw a picture

2. Write a formula (area, volume, Pythagorean theorem)

3. take derivative of both sides w/ respect to time (dx/dt or dy/dt)

4. Plug in what you know and solve for the remaining quantity

equation of a tangent line

y-y₁=m(x-x₁)

L’Hospital’s Rule

If limit x approaches c f(x)/g(x) results in 0/0 or +-infinity/+-infinity, then

limit x → c f(x)/g(x) = limit x → c f’(x)/g’(x)

Mean Value Theorem

If f(x) is continuous on [a,b] and differentiable on (a,b), then there exists a value c, a<c<b, such that f’(c) = f(b) - f(a)/ b - a.

Instantaneous rate of change = average rate of change.

Rolle’s Theorem

If mean value theorem and f(a) = f(b), then

there exists at least on c in (a,b) such that f’© = 0

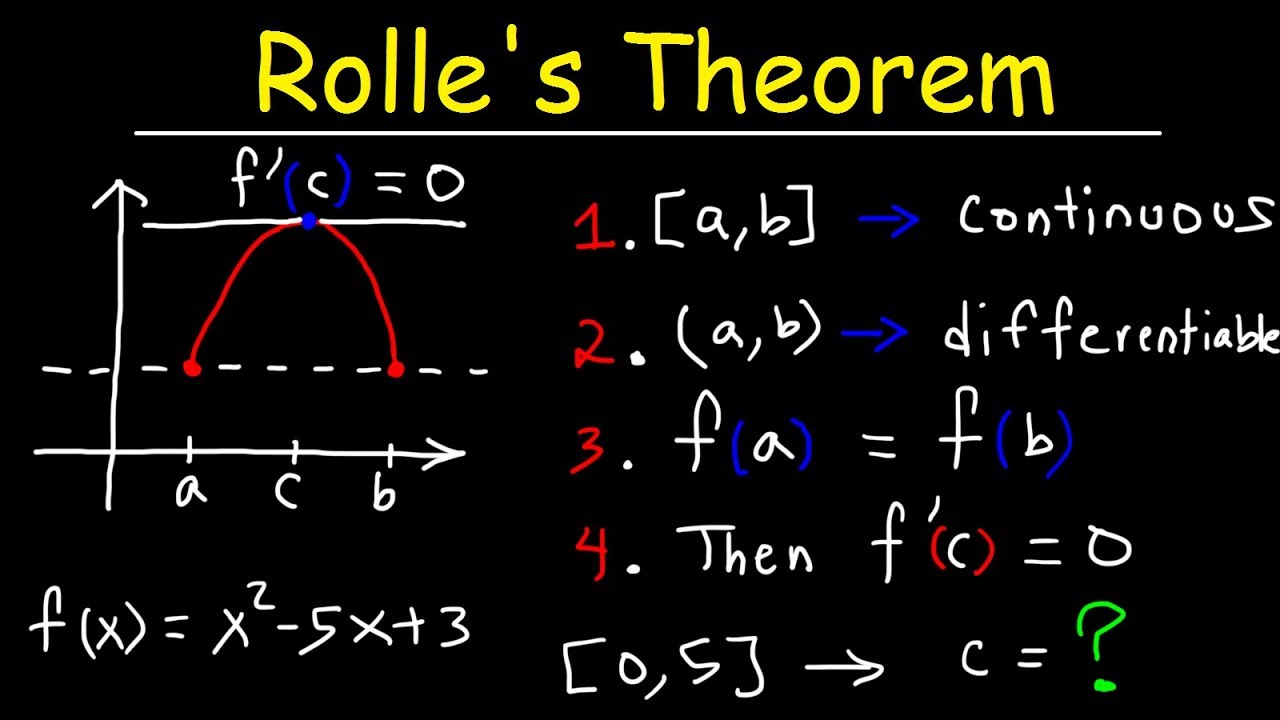
Extreme Value Theorem

If a function f(x) is continuous on [a.b], then f(x) must attain a maximum and minimum value on [a,b], which occurs at critical points or absolute extrema points. (DOES NOT NEED TO BE DIFFERENTIABLE)

First Derivative Test (relative extema)

If f’(x) > 0, f(x) is increasing

If f’(x) < 0, f(x) is decreasing

1. Find the critical values f’(x) = 0 or does not exist

2. Create a sign chart, plug in x values before, between, and after critical values into f’(x).

Candidate Test (Absolute Extrema)

1. Find critical values f’(x)=0 or does not exist

2. Make a table with critical values and given intervals

3. Solve for those x values in f(x)

Second Derivative

If f”(x)>0, f’(x) is increasing, f(x) is concave up

If f”(x)<0, f’(x) is decreasing, f(x) is concave down.

POI occurs when concavity changes signs and indicates f’(x) has a relative maximum.minimum

Second Derivative Test

1. Find critical values f’(x)=0 or does not exist

2. Calculate the Second Derivative: Find the function's second derivative.

3. Evaluate the Second Derivative at the Critical Points: Substitute each critical point into the second derivative.

4. Analyze sign

   1. f”(x) < 0 → relative maximum /\

   2. f”(x) > 0 → relative minimum v

Left Riemann Sum

∑_(i=1)^n f(x_i) * Δx = Δx[f(1)+f(3)+f(5)+f(7)]

Δx = b-a/n

Right Riemann Sum

∑ f(xᵢ) Δx = Δx[f(3+f(5)+f(7)]

If f(x) is increasing,

A left Riemann Sum gives an underestimate, and a Right Riemann Sum gives an overestimate.

If f(x) is decreasing,

A left Riemann Sum gives an overestimate, and a Right Riemann Sum gives an underestimate.

midpoint Riemann sum

∑_(i=1)^n f(Xi -1 = Xi/2) * Δx

Trapezoidal Sum

A=1/2h(b₁+b₂)

½ Δx [ f(1) + 2f(3) + 2f(5) + f(7)]

If f(x) is concave up,

a midpoint riemann sum gives an underestimate and a trapezoidal sum gives an overestimate

If f(x) is concave down,

a midpoint riemann sum gives an underestimate and a trapezoidal sum gives an overestimate

Antiderivative

F’(x) = f(x)

If F(x) is the antiderivative of f(x), then

∫ab​f(x)dx=F(b)−F(a)

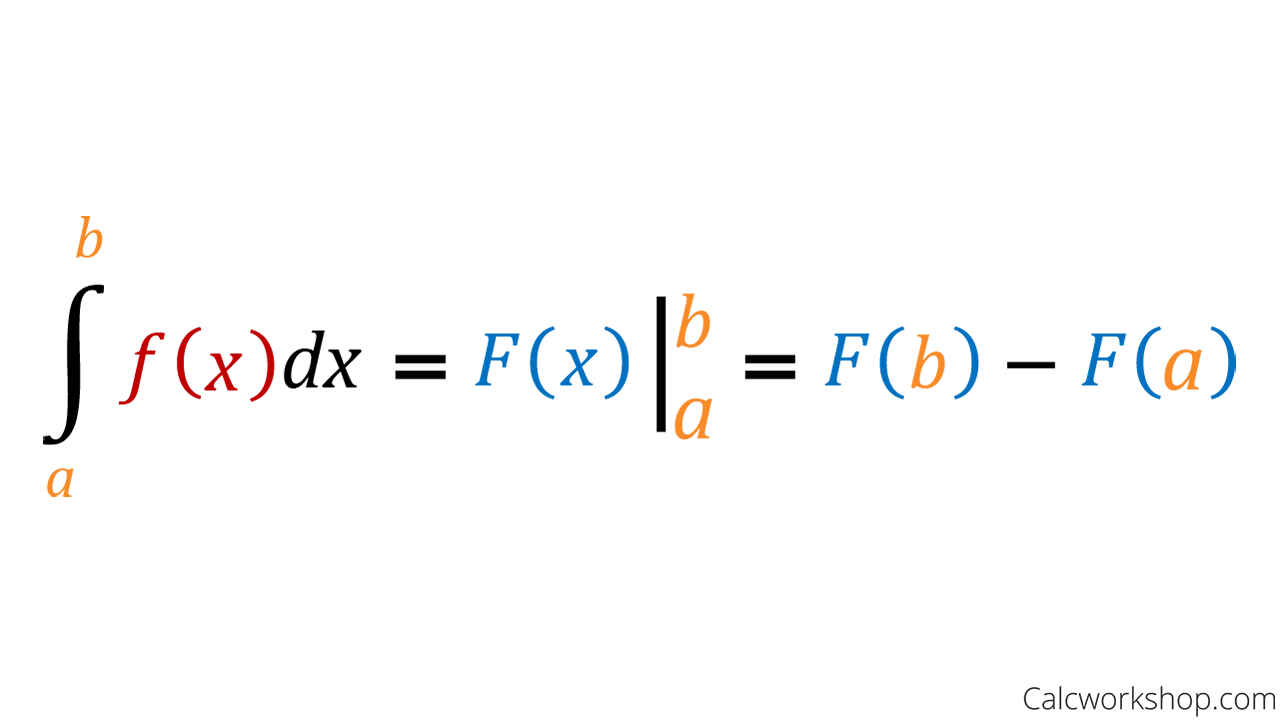
If f is continuous on the interval [a,b] and F(x) = integral a → b f(t) dt, then

F’(x) = f(x)

the rate of change is proportional to the quantity

y= Ce^kt

1/b-a integral a → b f(x) dx

the average value of a continuous function f(x) on [a,b] is

Area between curves

A_r= integral a → (f(x)-g(x))dx or A_r= integral a → b (f(y) - g(y)) dy

Area of a square

s²

Area of a triangle

½ bh

Area of Equilateral Triangle

(sqrt 3 /4)s²

Area of Semicircles

½ pie r²

Area of rectangles

bh

Area of trapezoid

½ h (b₁+b₂)

Perpendicular to the x-axis cross-sections

v = integral a→b A(x)dx

Perpendicular to the y-axis cross-sections

v = integral a→b A(y)dy

Disk

The axis of revolution is a boundary of the enclosed region

Disk Area

pie r²

Disk radius

f(x) or the x value (distance from curve)

Disk Volume

pie integral a→b r² dx or dy

Washer

There is space between the axis of revolution and the enclosed region

Washer Area

pie(R²-r²)

Washer R radius

Furthest function minus axis of revolution

Washer r radius

closest function minus axis of revolution

Washer Volume

pie integral a→b (R²-r²) dx or dy

0

1,0

pi/6

sqrt 3/2, ½

pi/4

sqrt 2/2 sqrt 2/2

pi/3

1/2, sqrt 3/2

pi/2

0,1

pi

-1,0

3pi/2

0,-1