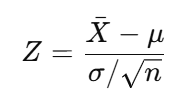Equations from Lecture 6: Sampling Distributions

Population Mean

• μ: True mean of the population

• N: Total number of individuals in the population

• Xᵢ: Value of the i-th individual in the population

Use: Describes the average value of a characteristic (e.g., height, weight) across the entire population.

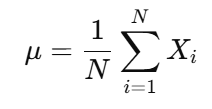
Population Variance

• σ²: Variance of the population

• Xᵢ: Individual value

• μ: Population mean

Use: Measures how spread out the values are in the population

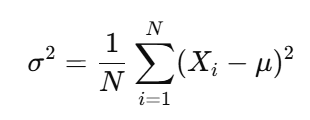
Sample Mean

• \(\bar{X}\): Mean of the sample

• n: Number of individuals in the sample

• Xᵢ: Value of the i-th individual in the sample

Use: Estimates the population mean using a subset of data.

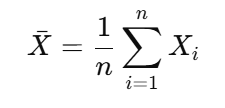
Sample Variance

• s²: Sample variance

• \(\bar{X}\): Sample mean

• Xᵢ: Individual sample value

Use: Measures variability within the sample. The denominator is \(n - 1\) to correct for bias (Bessel’s correction).

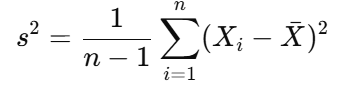
Mean of the Sampling Distribution

• E\(\bar{X}\)]: Expected value of the sample mean

• μ: Population mean

Use: The average of all possible sample means equals the population mean.

Variance of the Sampling Distribution

• Var\(\bar{X}\)): Variance of the sample mean

• σ²: Population variance

• n: Sample size

Use: Shows how much the sample mean varies from sample to sample.

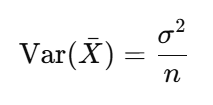
Standard Error of the Mean (SEM) 

• SEM: Standard deviation of the sample mean

• σ: Population standard deviation

• n: Sample size

Use: Quantifies how far the sample mean is likely to be from the population mean.

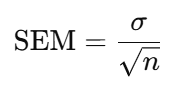
Adjusted Variance of Sample Mean for finite population

• N: Population size

• n: Sample size

• σ²: Population variance

Use: Adjusts the variance when sampling without replacement from a finite population.

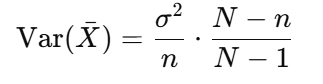
Central Limit Theorem (CLT)

• \(\bar{X}\): Sample mean

• N(…): Normal distribution

• μ: Population mean

• σ²/n: Variance of sample mean

Use: For large \(n\), the distribution of sample means becomes approximately normal—even if the population isn’t.

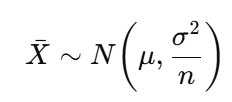
Standardized Z-score

• Z: Standardized score

• \(\bar{X}\): Sample mean

• μ: Population mean

• σ: Population standard deviation

• n: Sample size

Use: Converts a sample mean to a Z-score to find probabilities using the standard normal distribution.