Final Intro to log

A valid argument is one in which it is necessary that,

if the premises are true, then the conclusion is true.

deductive argument

• If you intend to make the conclusion “guaranteed” to be true

• one in which it is claimed that the conclusion follows necessarily from the premises

inductive argument

• If you intend to make the conclusion “probably” true

• one in which it is claimed that the premises make the conclusion prob

validity

An argument is valid if and only if it is impossible for the conclusion to be false given the premises are all true.

Soundness =

valid argument + all true premises

an argument is sound if and only if

it is valid and it contains all true premises

Validity is only about the

“relationship between the premises and the conclusion” regardless of the actual content

If valid, it is IMPOSSIBLE

the conclusion to be false given the premises are true

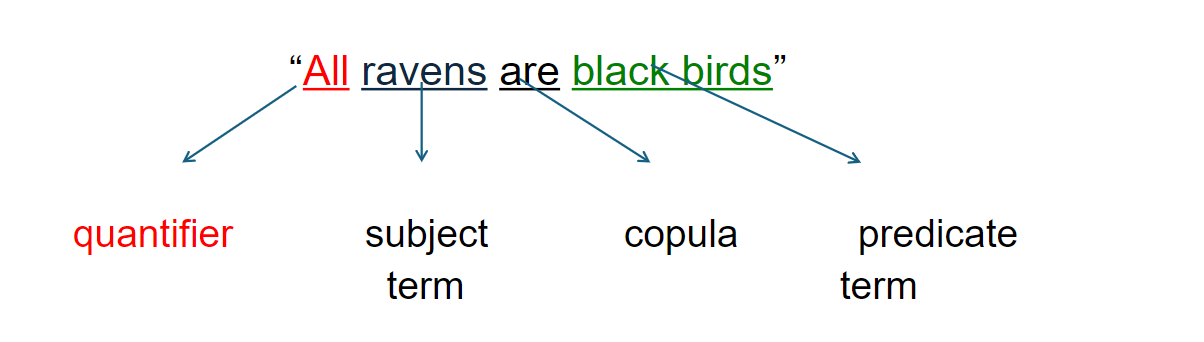
quantifier

A: All / E: No / I: Some / O: Some

copula

are, are, are, are not

Four components of a categorical statement

Subject, Predicate, Quantifier, Copula

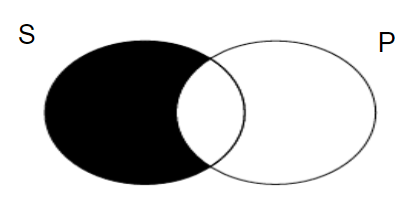
all S are P

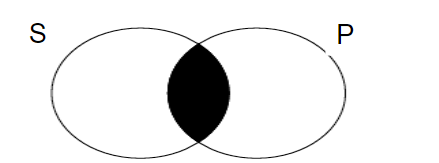
No S are P

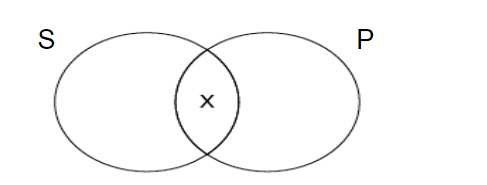
Some S are P

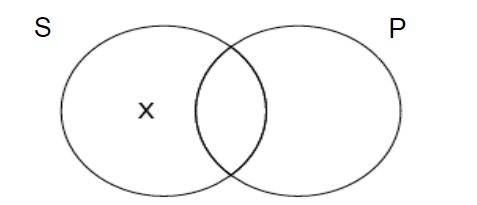
Some S are not P

A condition is sufficient if

whenever it is met, the outcome is guaranteed

a condition is necessary if

the outcome cannot happen without it

negation

connective/operator: not
symbol: ~

conjunction

connective/operator: and, but, however, furthermore, moreover, yet
symbol: &

disjunction

connective/operator: or, unless
symbol: v

conditional

connective/operator: if then, only if, so, necessary cond., sufficient for
symbol: —>

biconditional

connective/operator: if and only if, just in case, just if, necessary and sufficient
symbol: ←→

inductive argument will never be

valid, no matter how plausible, because it appeals to authority, it’s about credibility

truth table for P & Q

P | Q | P & Q

T | T | T

T | F | F

F | T | F

F | F | F

truth table for P v Q

P | Q | P v Q

T | T | T

T | F | T

F | T | T

F | F | F

truth table for P —> Q

P | Q | P —> Q

T | T | T

T | F | F —> if antecedent is false, then P —> Q is true

F | T | T

F | F | T

truth table for P ←→ Q

P | Q | P ←→ Q

T | T | T

T | F | F

F | T | F

F | F | T