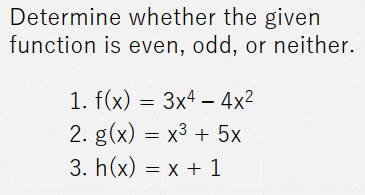DISCRETE MATH CHAPTER 4 REVIEWER
1/22
Earn XP
Description and Tags
Flashcards about Relations and Properties of Relations based on lecture notes.
Name | Mastery | Learn | Test | Matching | Spaced |
|---|
No study sessions yet.
23 Terms
FUNCTION
A is a special relation which stresses that no two ordered pairs should have the same first component or domain.
function kapag walang magkaparehong ordered pair for the domain, and all the domain ay magagamit
all functions are relations
"f of a equals b."
"f is a function from A to B.
f(a)=b: This reads as "____________" It means that the function f takes an element a from set A and assigns it to a unique element b in set B.
f:A→B: This reads as "____________" It tells us the overall relationship between the two sets: the function f maps elements from set A to set B.
Rule Form
set builder notation, A function is a rule that makes a relation between two sets of elements
such that to each element in the first set there connects one and only one element in the second set.
lahat ng element ng first set ay dapat konektado sa iisa lamang na element sa 2nd set
Set Form
set of ordered pairs (a, b) with the property that no two ordered pairs have the same first component (called the domain a) and different second component (called the range b).
walang 2 ordered pairs na same ng domain, at dapat magkaiba ng range
F - function (different domains, used only once), and all elements are used
G - not a function (same domain, 1and 1)
H - not a function (not all elements re used)
Suppose A = {1,2,3,4} and B = {1,2,3,4,5}. Let
• f = {(1,2), (2,3), (3,4), (4,5)}
• g = {(1,2), (1,3), (2,4), (3,5), ( 4,5)}
• h = {(1,1), (2,2), (3,3)}, be a function from A
to B.
Function Notation
The notation f(x) read as “f of x”, “f at x” or “the value of f at x” is the number in the range of the function f to which the domain value x is paired.
means f(x) = y or f(a) = b
co domain
preimage
range
domain
✓ If f is a function from A to B, we say that A is the domain of f and B is the ______ (range) of f.
✓ If f(a) = b, we say that b is the image of a and a is a ________ of b.
✓ The range of f is the set of all images of the elements of A.
image = ______?
pre image =________?
function since all elements are used and not repeated

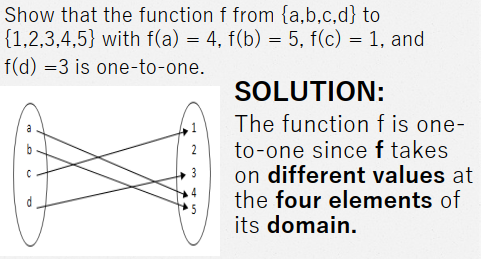
One-to-one Functions
A function f is said to be one-to-one or injective, if and only if f(x) = f(y) implies that for all x and y in the domain of f. A function is said to be an injection if it is one-to-one.
one domain is partnered to one range only, bawal maulit
its okay if not all range have pair
one to one dahil one domain and one range + function
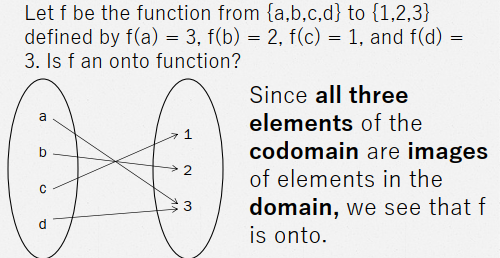
Onto Functions
A function f from Ato B is called onto or surjective, if and only if for every element b ∈ B there is an element a ∈ A with f(a) = b. A function f is a surjection if it is onto.
1 domain is used, and all range ay may pair
pwedeng maulit si range, but bawal dumoble ang domain
all codomain (range) ay nasakop
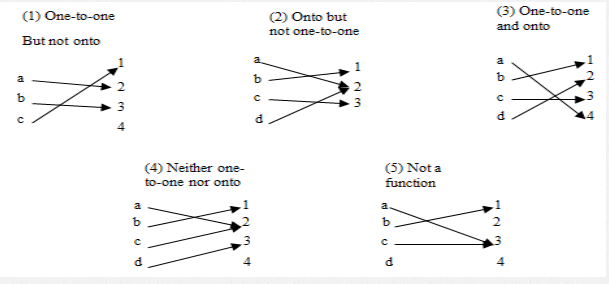
all domain ay nagamit, but not all range ay nasakop
naulit sa 2 ang a and d, but nasakop naman lahat ng range
all domain ay nagamit and di naulit, all range ay nasakop
naulit ang domain, and hindi nasakop lahat ng range
di nagamit ang element D
Evaluation of Functions
Function can be evaluated by substituting a specified input value into the given operation.


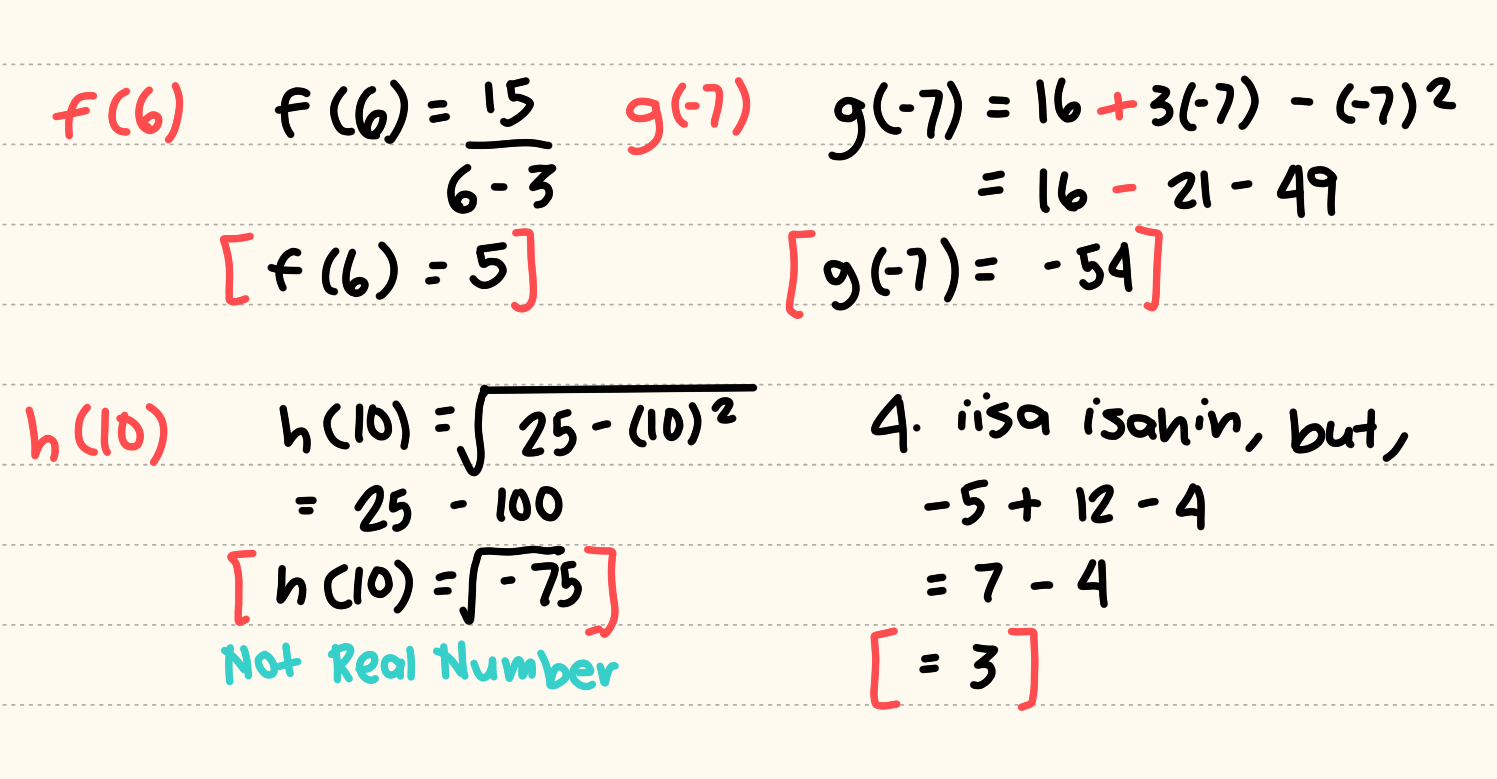
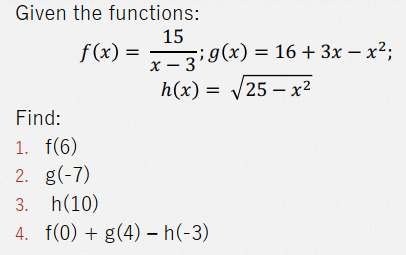
Operations on Functions
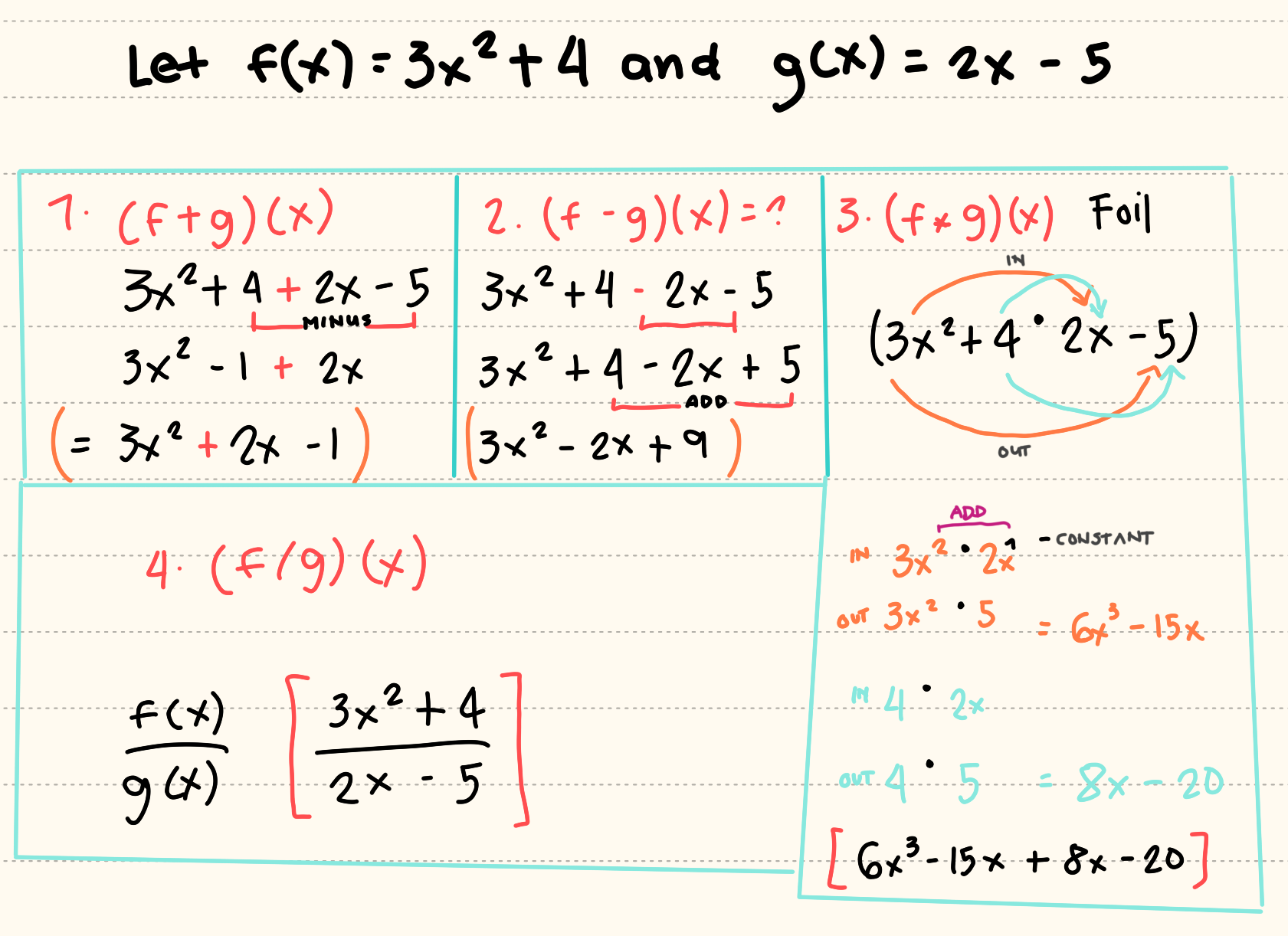
Let f and g be functions from A to R. Then the sum “f + g”, the difference “f – g”, the product “f * g” and the quotient “f / g” are functions
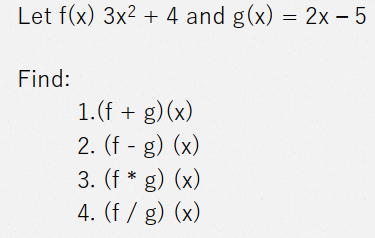
Composition of Functions
The composition of functions f and g, denoted by
f o g, is defined by f o g = f(g(a)).
g o f is defined by g o f = g(f(a))
function {(a,b)(b,c)(c,a)}
function {(a,3)(b,2)(c,1)}
✓ (f o g) (a) = f(g(a)) = f(b) = 2
✓ (f o g) (b) = f(g(b)) = f(c) = 1
✓ (f o g) (c) = f(g(c)) = f(a) = 3
Let g be the functions from the
set {a,b,c} to itself such that
g(a) = b, g(b) = c and g(c) = a.
Let f be the function from the set
{a,b,c} to the set {1,2,3} such that
f(a) = 3, f(b) = 2; and f(c) = 1.
✓What if f o g? g o f?
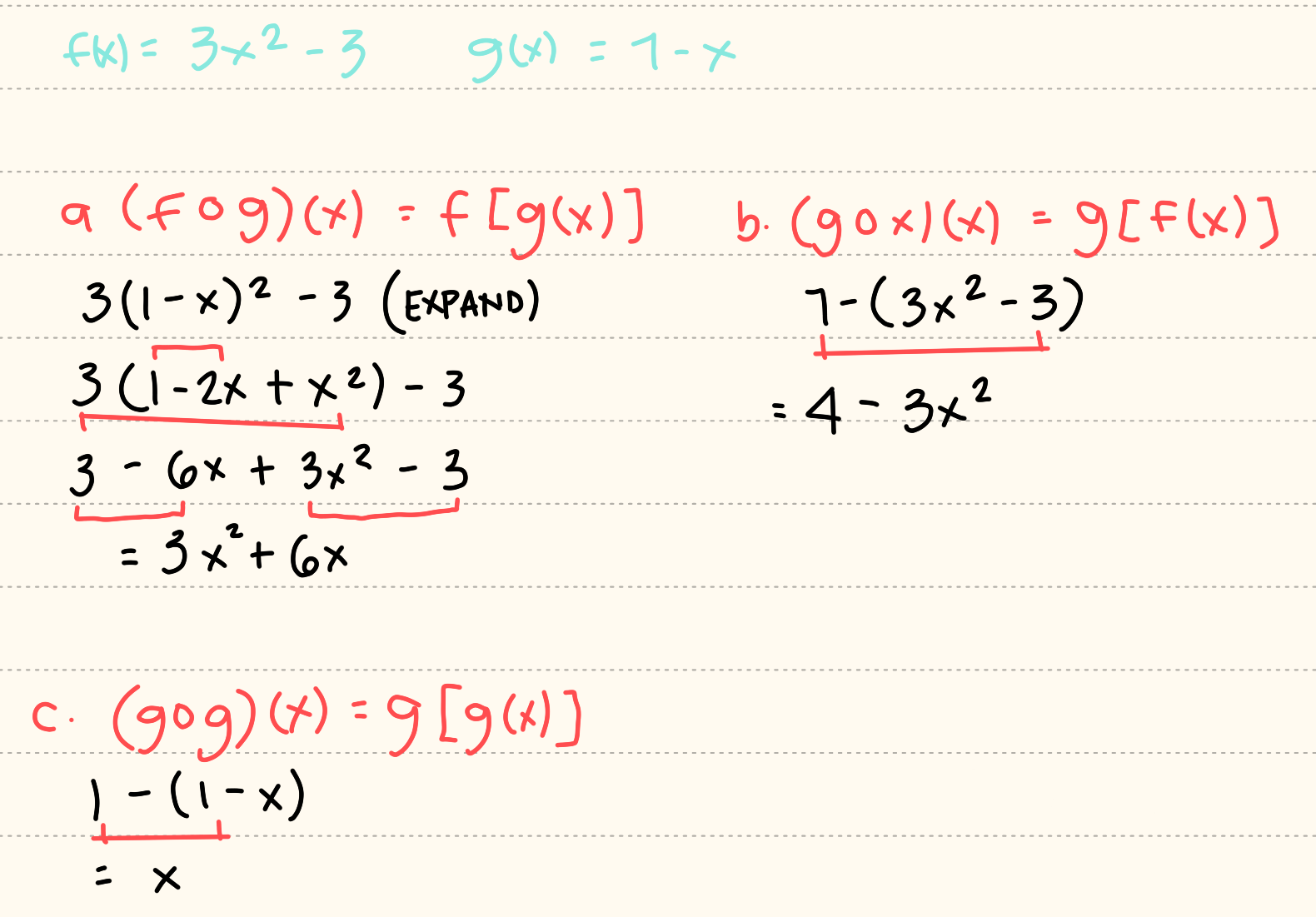
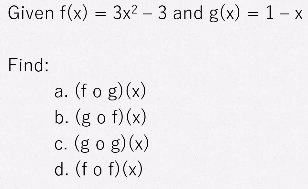
f(g(x)).
f(3x+2)
f(3x+2)=2(3x+2)+3
=6x+4+3
=6x+7
So, (f o g) (x)=6x+7.
g(f(x)).
g(2x+3)
g(2x+3)=3(2x+3)+2
=6x+9+2
=6x+11
So, (g o f) (x)=6x+11.
LALABAS SA QUIZ 4
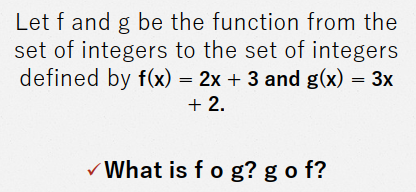
Odd and Even Functions
a. the function is even whenever f(-x) = f(x)
kapag ang f(x) ay pinalitan ng variable na f(-x) at bumalik sya sa original nya na form f(x)
b. the function is odd whenever f(-x) = -f(x)
kapag ang f(x) ay pinalitan ng variable na f(-x) at ang buong function ay bumaliktad din f(-x)
c. the function is neither even nor odd if (a) and (b) fail to hold
1. f(x) = 3x4 – 4x2
f(-x) = 3(-x)4 – 4(-x)2
= 3x4 – 4x2 = f(x)
thus, f is even.
2. g(x) = x3 + 5x
g(-x) = (-x)3 + 5(-x)
= -x3 – 5x
= -(x3 + 5x) = - g(x)
thus, f is odd.
3. h(x) = x + 1
h(-x) = (-x) + 1
= -x +1
✓ h(-x) ≠ h(x), so is not even.
✓ Also, h(-x) ≠ -h(x), so h is not odd.
✓ h is neither even nor odd.