IB Chemistry HL: Models of the particulate nature of matter

Matter

Any substance that occupies space

Pure substance

Substances that have a definite and uniform chemical composition of made of one element or compound only

Element

Substances composed of one type of atom only

Compound

Substances composed of two or more kinds of atoms in a fixed ratio.

Mixture

A combination of two or more pure substances that retain their individual properties

Homogenous mixtures

Where the substance has a uniform composition, meaning that the arrangement of the substances is equal throughout

heterogenous mixture

Mixtures where the arrangement of the substances within it are NOT the same throughout. This means they have a non-uniform composition.

Filtration

Separation technique where a mixture is poured through a filter paper. It separates insoluble solids from a liquid

dissolution/solvation

Separation technique where mixture is added to water or an organic solvent in order to separate insoluble substances from soluble ones

Crystalisation

Separation technique where the mixture (often a solution) is heated up to form crystals. Then the solution is left to cool and evaporate leaving pure crystals of the solute.

Evaporation/distillation

separation technique where a solution is heated until one or more of its components vaporize(s), This separates solids/non-volatile liquids away from volatile liquids

Paper chromatography

Separation technique used to separate 2 soluble liquids. The mixture is placed on a piece of paper, where one side is submerged in water or a solvent. These components move upwards along the paper

Bond energies during change of state

heating (solid → liquid → gas) = energy absorbed

Cooling (gas → liquid → solid) = energy released

The nuclear symbol notation

A way to represent isotopes of elements, showing the element's atomic number and mass number. It is typically written as the element's symbol with the mass number as a superscript and the atomic number as a subscript.

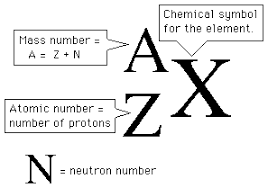
Types of sub atomic particles

• Proton (p⁺): 1amu

• Neutron (n⁰): 1 amu

• Electron (e^-): ~0 amu

These subatomic particles are found in all atoms, the number of protons is shown by the atoms atomic number, the total mass of the atom is showed by the atomic mass.

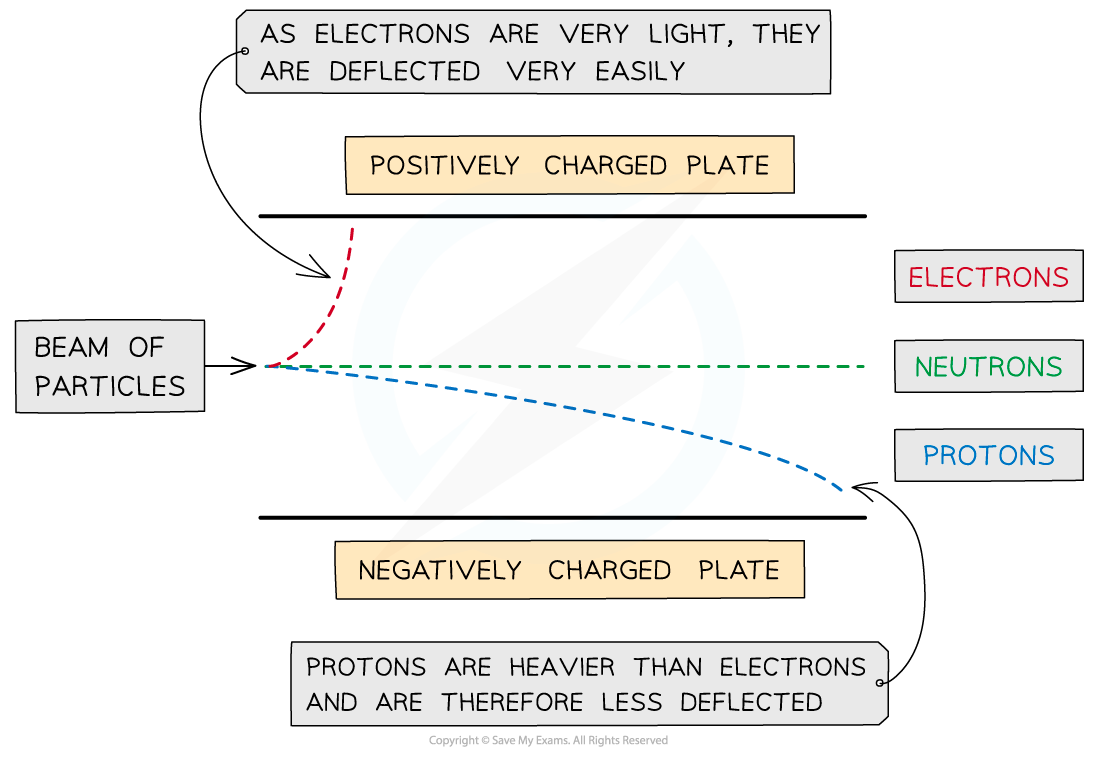
Reaction of subatomic particles to a charged plate

Protons move gently to the -ive plate
Electrons move sharply to the +ive plate due to a smaller mass
The neutron is unaffected

Isotopes

Atoms of the same element with the same number of protons but different numbers of neutrons, resulting in different mass numbers. Isotopes exhibit similar chemical properties but may have different physical properties.

Relative atomic mass

This is the mass of an element relative to all its isotopes. it is calculated using these formula:

• ∑(relative abundance x mass)/100

• ∑(mass x Ratio)/∑ Ratio

Or if a mass spectrum was used, use…

• ∑(m/z ratio x relative abundance)/∑ abundance

• ∑(m/z ratio x relative intensity)/∑ intensity

NB: the difference between abundance and intensity is that the abundance is a percentage, and the intensity is the same as a ratio. It just has a different name.

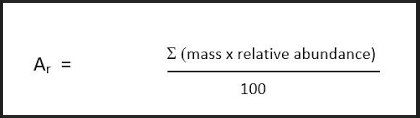
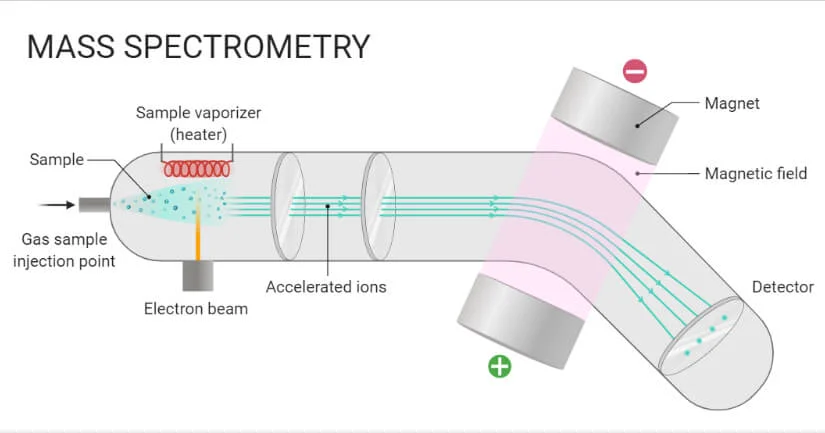
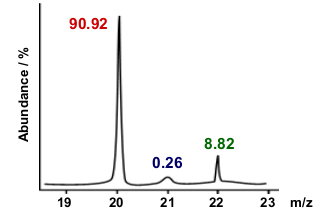
Mass spectrometry / Mass Spectroscopy

Analytical technique that uses a mass spectrometer in order to detect the abundance of isotopes in a sample

The result of a mass spectrometry is a mass spectrum.

Mass spectrum

This is the result of a Mass spectrometry

• The largest peak is the Base Peak

• The Last peak given on the graph is the molecular ion peak

This is used to

• determine the identity of isotopes (initially)

• calculate Relative atomic, isotopic and molecular masses

• Find the structural formula and characteristics of compounds

How a Mass spectrometer works

1. The sample is injected into the instrument and vaporized so that individual atoms can be analyzed

2. The atoms within the sample are then bombarded by high energy electrons. As a result the atoms lose some of their electrons to form cations.
   eg: Cu(g) + e- → Cu+ + 2e-

3. The resulting ions are then acceleratied by an electric field

4. Then deflected by a magnetic field.

5. When ions hit the detector, their m/z values are determined and passed to a computer which then generates the mass spectrum of the sample, in which relative abundances of all detected ions are plotted against their m/z ratios

what affects the degree of deflection

This depends on the mass to charge ratio (m/z ratio). Particles with no charge are not affected by the magnetic field within the mass spectrometer, and therefore dont reach the detector. The species with the lowest m and the highest z will be deflected the most.

Using a mass spectrum to calculate RA

There are 2 formula:

• ∑(m/z ratio x relative abundance)/∑ abundance

• ∑(m/z ratio x relative intensity)/∑ intensity

The general way to do it if the graph is with you is:
∑(x ⋅ y)/∑ y
Sum of all corresponding x and y values divided by the sum of the corresponding y values.

Electromagnetic radiation

Most subatomic particles behave as particles and obey the physics of waves. This forms the equation that relates the frequency, wavelength and velocity of a wave together:

V = λf

λ = wavelength
v= velocity
f= Frequency

Einstein-Planck Relation

This states that Energy released by a wave (E) is equal to
The Planck constant (h) multiplied by the frequency (f or v)

• E = hf

• E = hv

both f and v are frequency, some text books may use one while others may use the other.

The Planck Constant

This constant has the symbol “h” and is equal to 6.63 × 10^-34 This doesn’t necessarily have to be memorized, though it will be useful.

Emission Spectra

A pure gaseous element subjected to a high voltage under reduced pressure will glow — ie. emit light. When this light passes through a prism, it produces a series of lines onto a black background. This is an emission spectrum. In contrast, when a cold gas is placed between a prism and a white light, series of dark lines within a continuous spectrum will appear. This is an absorption spectrum.

Electrons release photons when returning to a lower energy level. This is as the electrons emit energy to their surroundings, and therefore emit light, therefore forming an emission spectrum.

When they return back to a lower energy level, they absorb energy i

• The wavelength of emitted light depends on the element

• The colour of light depends on the frequency.

  • The frequency of the wave will depend on which shell the electron is returning to

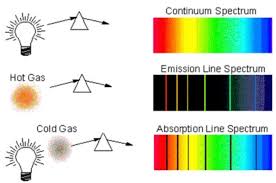
line spectrum

This is made by the light produced through the emission spectra of an atom, it is not continuous but consists of discrete lines, hence the name “line spectrum“.

The reason that it forms discrete lines is as electrons are only found in shells a set distance away from the nucleus. A continuous spectrum would suggest that electrons can exist anywhere around the nucleus.

Atomic emission spectra

The distance between shells 1 & 2 is greater than shells 2 & 3. This means that the distance between shells get smaller. Therefore, the amount of energy released when moving down shells gradually get smaller the higher the energy level.

Furthermore, as energy is directly proportional to frequency (E = hf and h is constant) the higher the electron shell numbers, the lower the frequency.

Lyman, Balmer and Paschen series

These are the names of the types of emissions of electromagnetic radiation caused by atomic emission of light.

• The Lyman series emits UV rays when an electron emits enough energy to move down to the 1st energy shell

• The Balmer series emits visible light when an electron emits enough energy to go to the 2nd energy shell

• The Paschen series emits Infrared rays when an electron emits enough energy to go to the 3rd energy shell

Principle energy levels

These are the standard electron shells around a nucleus. The maximum number of electrons an energy level can hold is 2n². where “n“ is the shell number.
These energy levels contain sub levels.

• When n = 1, there is 1 subshell: s.

  • maximum of 2 electrons in the 1st shell

• When n = 2, there are 2 subshells: s, p.

  • maximum of 8 electrons in the 2nd shell

• When n = 3, there are 3 subshells: s, p, d.

  • maximum of 18 electrons in the 3rd shell

• When n = 4, there are 4 subshells: s, p, d, f.

  • maximum of 32 electrons in the 4th shell

Note: There are only 4 types of subshell and no primary shell can contain more than one of each type.

Subshells

Each energy level has corresponding sub shell(s). the number of sub shells in an energy level is equal to the principle energy level number. Note there are only 4 subshells: s, p, d, and f

PRINCIPLE ENERGY SHELL	MAX NUM OF ELECTRONS (2n2)	NUMBER OF SUB SHELLS (usually equal to n)	SUB SHELLS
1	2	1	s
2	8	2	s, p
3	18	3	s, p, d
4	32	4	s, p, d, f

Orbitals

These are pairings of 2 electrons that spin in opposite directions.

• The electrons are organized one-by-one into their orbitals.

Each subshell can hold a different number of orbitals, therefore holding a different number of electrons

SUB LEVEL	MAX NO ELECTRONS	NO. ORBITALS
s	2	1
p	6	3
d	10	5
f	14	7

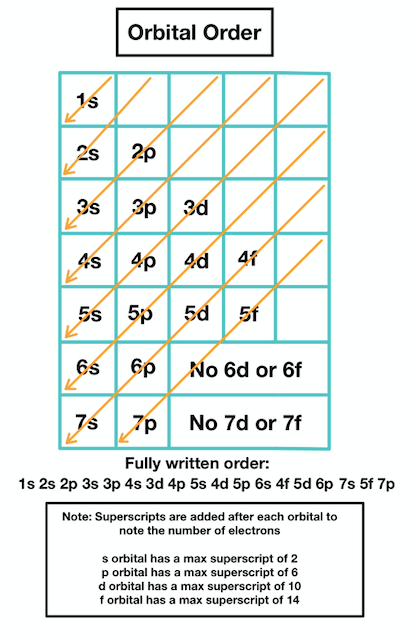
Order in which orbitals fill

1s, 2s, 2p, 3s, 3p, 4s, 3d, 4p, 5s, 4d, 5p, 4f

Note: The reason that 4s comes first is that the 4s subshell is closer to the nucleus than the 3d subshell. This is the same reason for the others

Hund’s Rule of maximum multiplicity

States that when assigning electrons to orbitals, electrons first seek to fill all the orbitals with similar energy.

Essentially, states that electrons will fill orbitals one by one, and will only add the second electron to an orbital when all orbitals in a subshell have the same number of electrons

Pauli’s exclusion principle

No 2 electrons in the same atom can have identical values for all 4 of their quantum numbers. This means that:

• no more than 2 electrons can occupy the same orbital

• 2 electrons in the same orbital must have opposite spins

Aufbau Principle

States that in the grounds state of an atom or ion, electrons first fill subshells of the lowest available energy.
For transition elements, the 4s subshell fills first EXCEPT chromium [Cr] and Copper [Cu]

• Copper [Cu] → [Ar] 3d¹⁰ 4s¹

• Chromium [Cr] → [Ar] 3d⁵ 4s¹

The reason for this is the electronic configuration is the most stable as the 3d subshell have an equal number of electrons in each orbital (2 electrons in each orbital for Cu, 1 electron in each orbital for Cr)

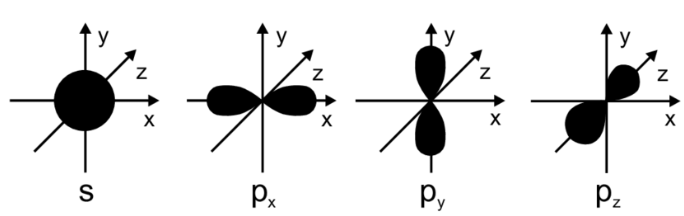
Shapes of orbitals

The s orbitals are in the shape of a sphere

The p orbitals are in the shape of an 8 and rotates so that it can be in all 3 states: p_x, p_y, p_z.

Ionization energy

This is the minimum energy required to eject an electron from a neutral atom. i.e: the energy required for an electron to escape an atom or reach the upper limit of convergence.

The first ionization energy (min energy required to eject the first electron from the atom) can be found through the use of the Einstein-Planck relation: E= hf

Example of the first ionisation energy:

X (g) → X⁺ + e^-

Limit of Convergence

The is the point where the electron shells appear to meet. Therefore this is the furthest point from a nucleus where an electron is affected

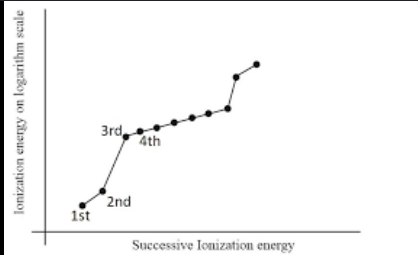
Ionization energy graph of magnesium

The successive ionization energies of an element increase:
1E₁ < 1E₂ < 1E₃.

This is because once you remove the outer electron from an atom, you form a positive ion.

Removing an electron from an ion is harder than from a neutral one as attractive forces increase because there is a greater difference in charge and because the electron gradually gets closer to the nucleus, and therefore experiences a stronger pull.

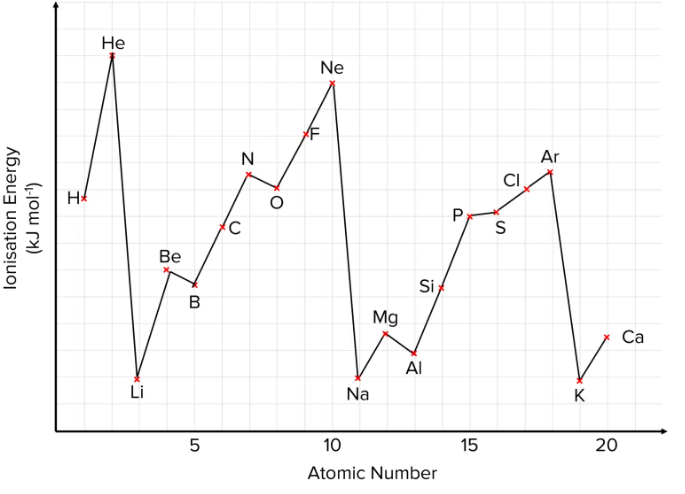
Factors that effect the variation of first ionization energy (between elements)

• the state of the orbitals of the last subshell

  • 2 electrons in each orbital (most stable)

  • 1 electron in each orbital

  • non equal number of electrons in each orbital (least stable)

• Distance from the nucleus.

  • the further away an electron is from the nucleus, the lower its first ionization energy, and vice versa

Mole

Unit for amount of a substance.

empirical formula

The most simplified version of a compound

Percentage composition

The amount of an element in a compound expressed as a percentage

How to find the emperical formula with percentage composition

1. percentage composition / mr

2. divide by smallest value within the ratio

Gas laws

Includes:

• Boyle’s law

• Charles Law

• Gay- Lussac’s Law

• The combined gas Law

• Avogadro’s Law

• The ideal gas law

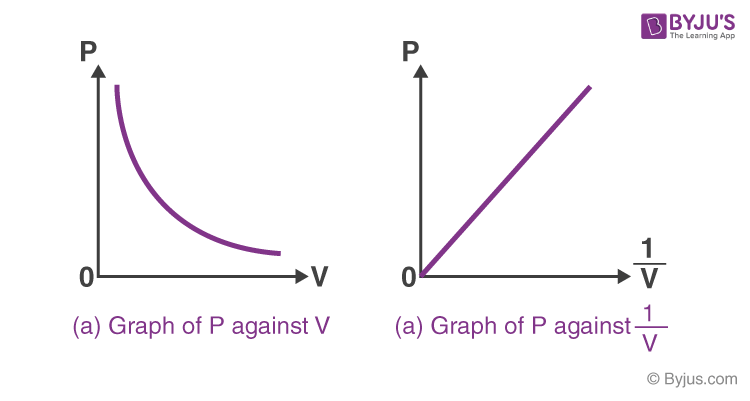
Boyle’s Law

P₁V₁ = P₂V₂

proof:
F = P x A

• force is constant due to equilibrium, therefore volume and pressure are inversely proportionate

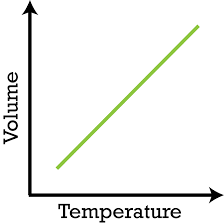
Charles Law

States that temperature is directly proportional to volume

• V ∝ T
  V = kT
  k= V/T

Therefore…
V₁ / T₁ = V₂ / T₂

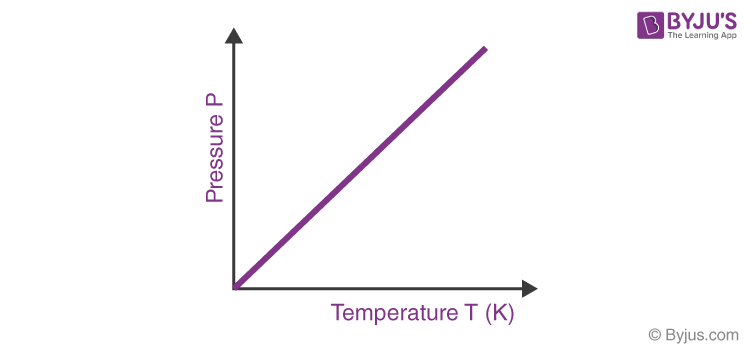
Gay- Lussac’s Law

States that Pressure is directly proportional to volume

• P ∝ T
  P = kT
  k= P/T

Therefore…
P₁ / T₁ = P₂ / T₂

The Combined Gas law

This is a combination of Boyle’s, Charle’s, and Gay-Lussac’s Laws, and only applies if the amount of gas is constant:

P₁ V₁ / T₁ = P₂ V₂ / T₂

Avogadro’s Law

1 mol of any gas takes up 24 dm³ at r.t.p and 22.7 dm³ at s.t.p

The Universal gas equation/ The ideal gas Law

PV = nRT

• P- Pressure (kPa)

• V- Volume (dm³)

• n- Number of Moles

• R- rate constant = 8.31 mol^-1 K^-1

• T- Temperature (kelvin)

Ideal Gases

This is a gas that obeys the ideal gas law, PV=nRT, under all conditions.

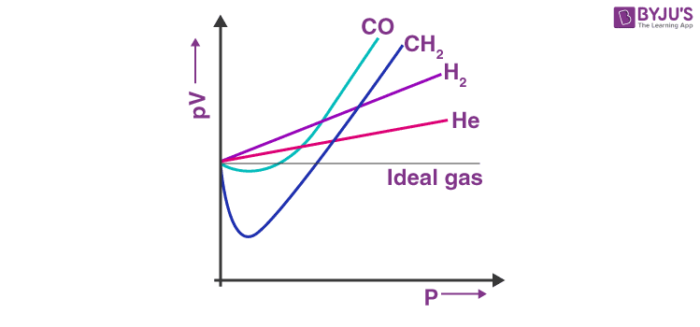
Real Gases

Real gases don’t always behave like ideal gases, so the graph will deviate.

For a gas to deviate from its Ideal gas behavior, there must be detectable intermolecular forces (hence the low temperature) and/or a significant volume of the gas must be occupied by the molecules themselves (high pressure). This commonly occurs at low temperatures, and high pressure.

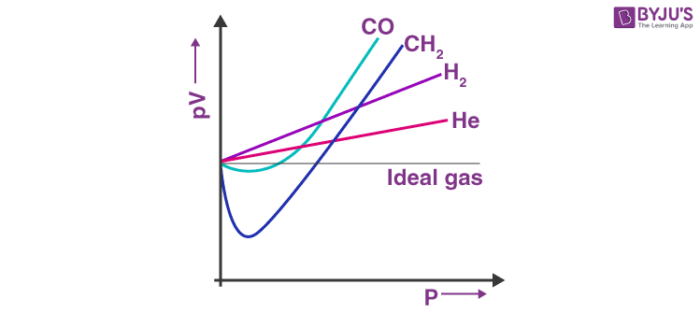
Examples of real gases

• N₂

• O₂

• H₂

• CO₂

=