2 Ridge Regression , Lasso Regression & ElasticNet Regression

Regularizatin techniques

how do we reduce the over fitting of linear regression

We use ridge regression

Ridge Regression formula

when we have overfitting the cost function will be

zero

Formulae of ridge Regression

when cost function is zero that means

data is Overfitting

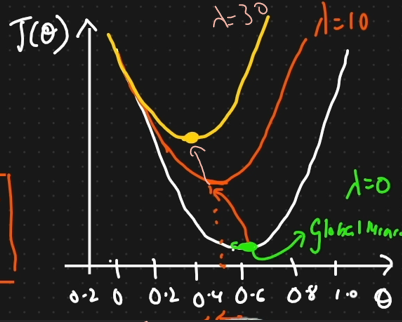
if we increase the lamda then ____ is shifted

Gradient decent curve is moved. This happen when lambda value increase.

Explain the difference between L1 and L2 regularization.

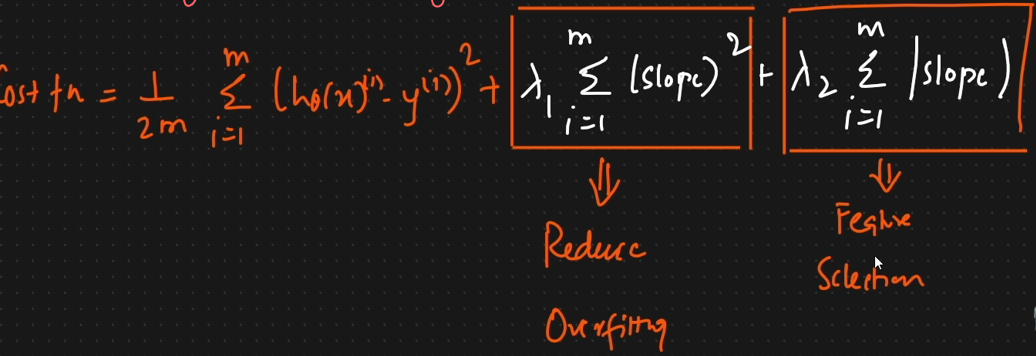
L1 Regularization (Lasso): Adds the absolute value of the weights to the loss function.

Encourages sparsity by shrinking some weights to zero, effectively selecting features.

Suitable for models where feature selection is important or many features are irrelevant.

L2 Regularization (Ridge): Adds the square of the weights to the loss function.

Encourages smaller, evenly distributed weights without eliminating them.

Ideal for models where all features are important and should contribute to predictions.

Sparsity: L1 leads to sparse models by zeroing out weights; L2 keeps all weights small but non-zero.

Optimisation: L1 can result in non-smooth optimisation, while L2 maintains smooth gradients, making it computationally easier.

If global minima should not move then lamda value should be

Zero

best fitted line is moved above or below depending on

Lamda function

Lasso Regression

The feature that is not important will be deleted automatically.

Formula of lasso Regression

Elastic Regression

This help in reduce the overfitting & feature Selection.

Formulae of Elastic net

What is regularization and why is it used in machine learning?

Regularization is a technique used in machine learning to prevent overfitting by adding a penalty to the model's complexity. It helps improve the model's generalization ability, ensuring it performs well on unseen data.

Regularization Type

L1 regularization (Lasso) and L2 regularization (Ridge).

How does regularization prevent overfitting, and why do we use techniques like L1 and L2? 

• L1 Regularization (Lasso):

  • Penalty: Adds the absolute value of the coefficients to the loss function.

  • Effect: Encourages sparsity, meaning it can drive some coefficients to zero, effectively performing feature selection.

  • Use Case: Useful when you suspect that only a few features are important.

• L2 Regularization (Ridge):

  • Penalty: Adds the squared value of the coefficients to the loss function.

  • Effect: Shrinks the coefficients but does not set them to zero, leading to a more evenly distributed set of weights.

  • Use Case: Useful when you want to keep all features but reduce their impact.

How Lasso Regression Performs Feature Selection:

Lasso regression uses L1 regularization, which adds a penalty equal to the absolute value of the coefficients. This penalty forces some coefficients to become exactly zero, effectively removing irrelevant or less important features. By shrinking less significant feature weights to zero, Lasso performs implicit feature selection while maintaining a simpler, more interpretable model.