Derivative Rules + Riemann Sums + Integration Formulas + Summation Notation + Properties of the definite integral + FTC
1/36
There's no tags or description
Looks like no tags are added yet.
Name | Mastery | Learn | Test | Matching | Spaced |
|---|
No study sessions yet.
37 Terms
(Derivative Rules) Product Rule
f(x)g’(x) + g(x)f’(x)
(Derivative Rules) Quotient Rule
(g(x)f’(x) - f(x)g’(x))/g(x)²
(Derivative Rules) Chain Rule
f’(g(x))g’(x)
General Riemann Sums
A ≈
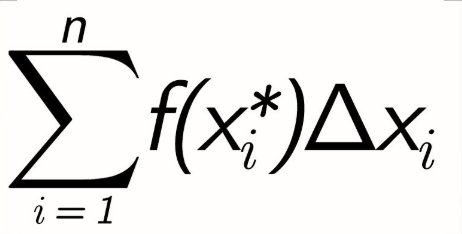
(Integration Formulas) ∫axcdx =
a · (xn+1)/(n+1) + c
(Integration Formulas) ∫sin(ax)dx =
(-1/a) cos(ax) + c
(Integration Formulas) ∫cos(ax)dx =
(1/a) sin(ax) + c
(Integration Formulas) ∫sec(ax)tan(ax)dx =
(1/a) sec(ax) + c
(Integration Formulas) ∫csc(ax)cot(ax)dx =
(-1/a) csc(ax) + c
(Integration Formulas) ∫sec²(ax)dx =
(1/a) tan(ax) + c
(Integration Formulas) ∫csc²(ax)dx =
(1/a) -cot(ax) + c
(Integration Formulas) ∫(1/x)dx =
ln|x| + c
(Integration Formulas) ∫eaxdx =
(1/a) eax + c
(Integration Formulas) ∫baxdx =
(1/a ln b) bax + c
(Integration Formulas) ∫1/(√1-(ax)²)dx =
(1/a) sin-1(ax) + c
(Integration Formulas) ∫1/(1+(ax)²dx) =
(1/a) tan-1(ax) + c
Definite Integral
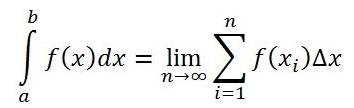
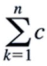
(Summation Notation) Constant Value Rule
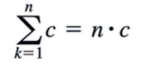
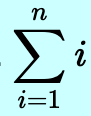
(Summation Notation)
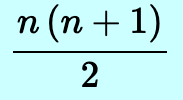
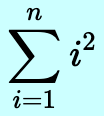
(Summation Notation)
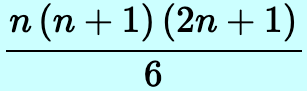
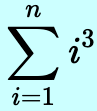
(Summation Notation)
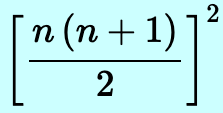
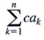
(Summation Notation) Constant Multiple Rule
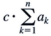
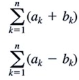
(Summation Notation) Sum/Difference Rule
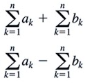
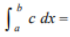
(Property of Definite Integral) Constant Multiple
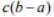

(Property of Definite Integral) Constant Multiple
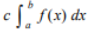
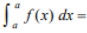
(Property of Definite Integral)
0
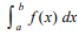
(Property of Definite Integral)
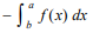
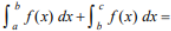
(Property of Definite Integral)
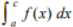
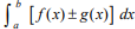
(Property of Definite Integral)
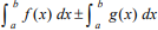
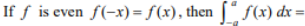
(Property of Definite Integral)
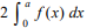
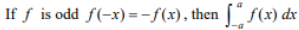
(Property of Definite Integral)
0
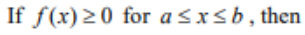
(Property of Definite Integral)
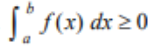
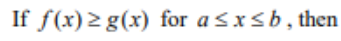
(Property of Definite Integral)
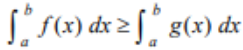
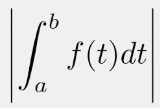
(Property of Definite Integral)
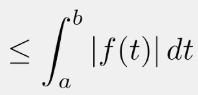
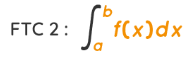
(FTC)

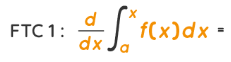
(FTC)
f(x)
(basically gives back original function)