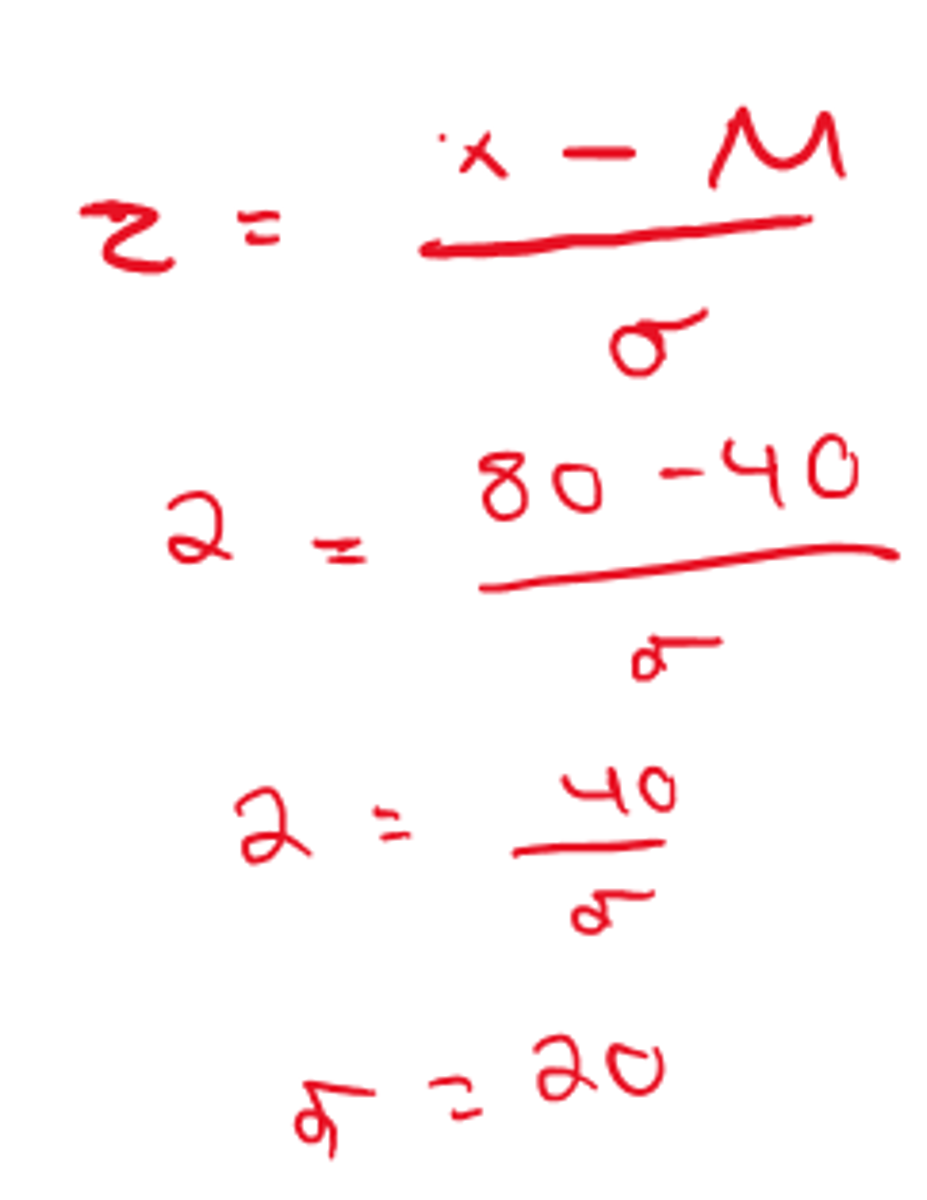HTHSCI 2S03 - Lecture: Joint Either/Or Probability, Probability Distributions, & Normal Distribution

Joint Either/Or Probability

Joint Probability

- P(A∩B) is the probability that events A and B will both occur

- Key to understanding joint probability is to know that the words “both” or “and” are usually involved in the question

Multiplication Rule - Joint Probability

- The Multiplication Rule is used to calculate joint probabilities

= P(B) x P(AlB)

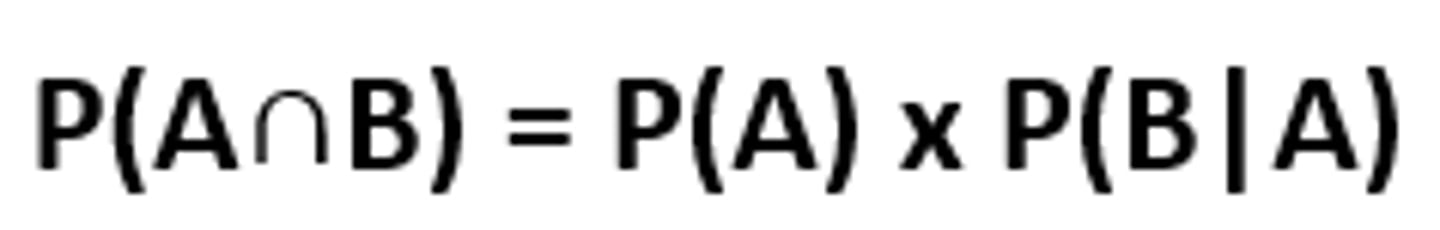
Joint Probability Example

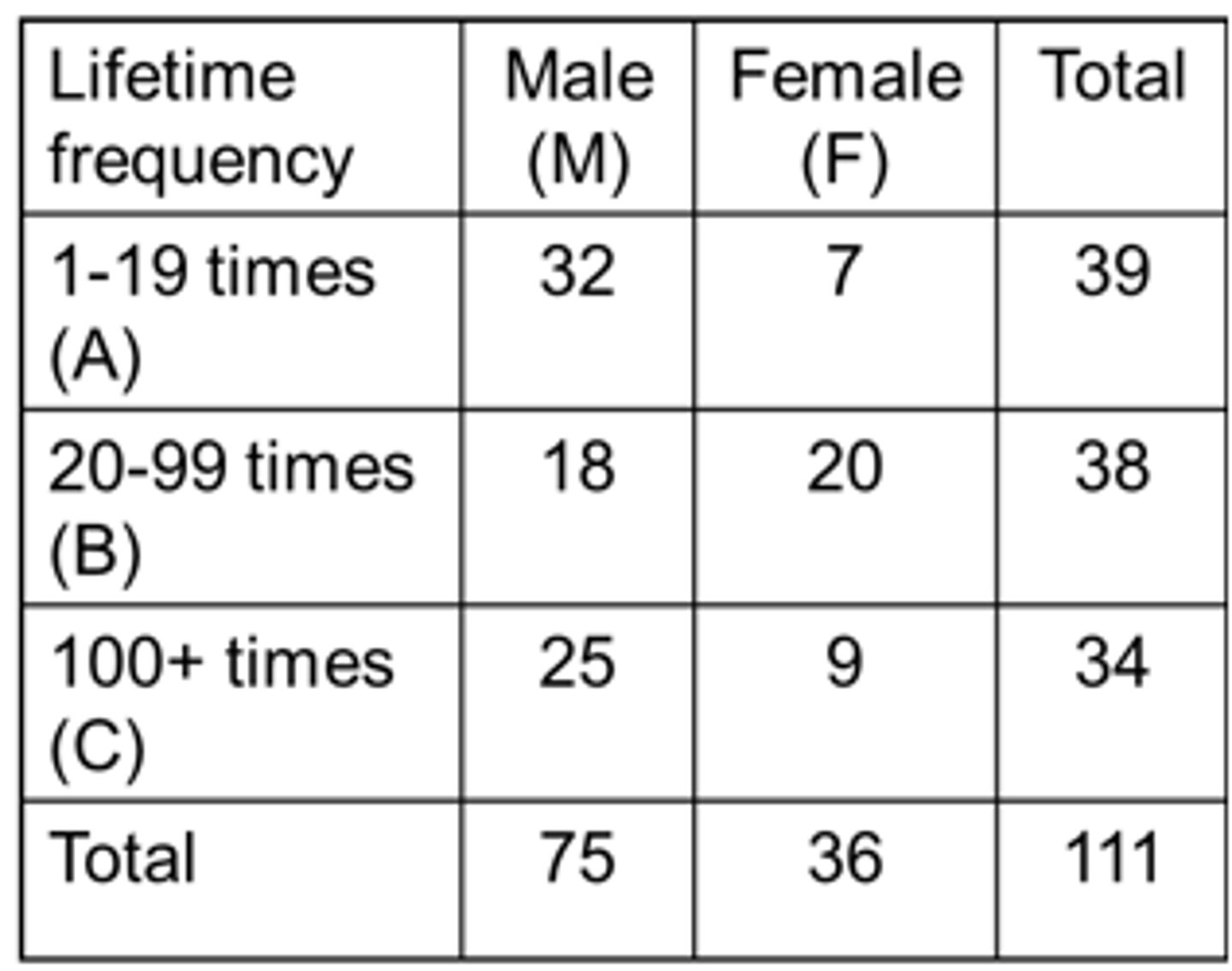
What is the probability that a person picked at random will be:

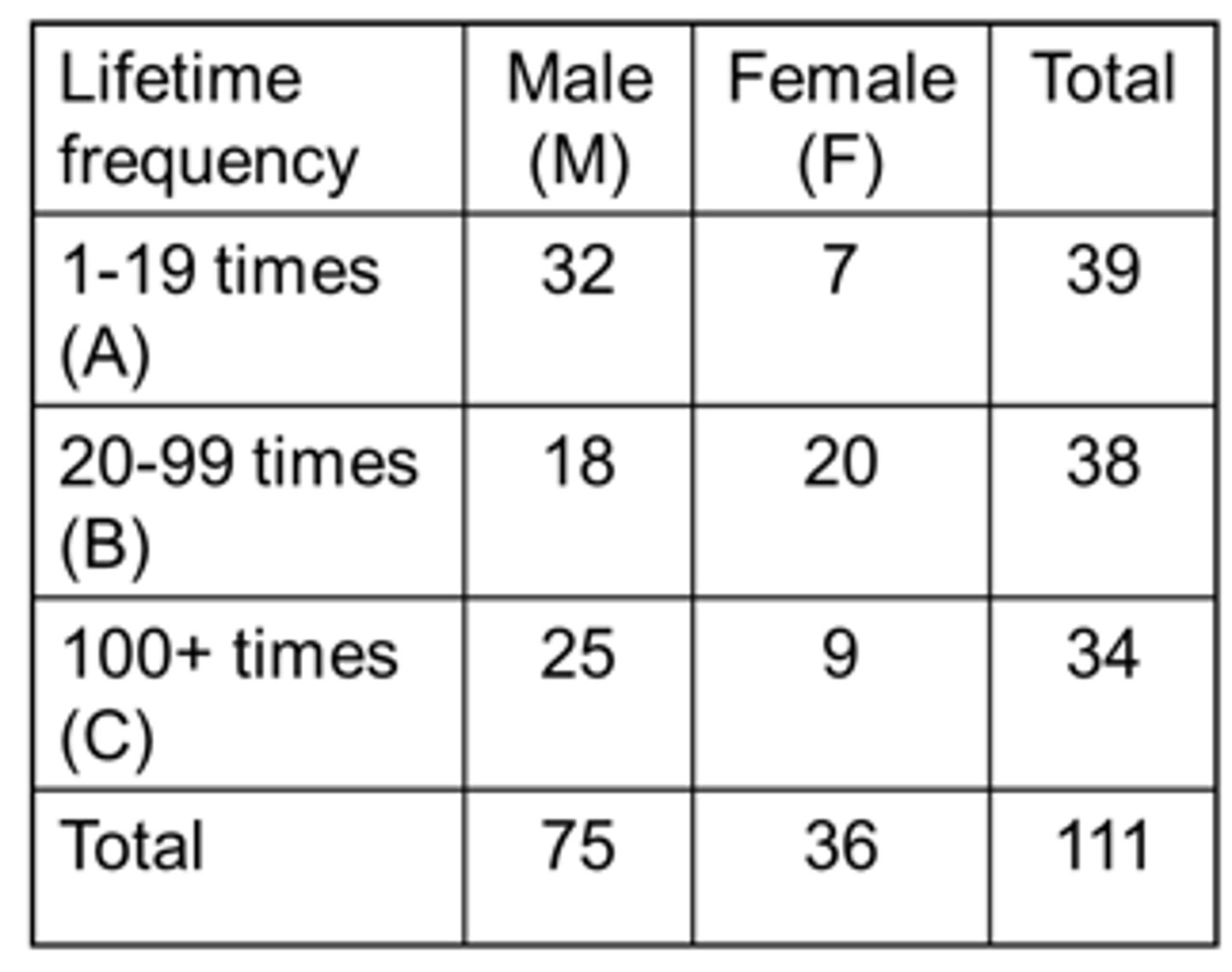
1. A male (M) and a person who used cocaine 1-19 times during their lifetime (A)?

P(M∩A) = P(M) x P(A|M)

= 75/111 x 32/75

= 0.288 or 28.8%

2. A female (F) and 20-99 times user (B)?

P(F∩B) = P(F) x P(B|F)

= 36/111 x 20/36

= 0.180 or 18%

Independent Events - Joint Probability

- Two events are independent when the occurrence of one does not change the probability that the other will occur

- Ex. Rolling a 3 on a die and flipping a tail on a coin (rolling a 3 does not affect the probability of flipping a tail)

If two events A and B are independent, then the conditional probabilities are simply the marginal probabilities:

- P(A|B) = P(A)

- P(B|A) = P(B)

For two independent events A and B, the joint probability simplifies to the product of the two marginal probabilities: Formula in picture

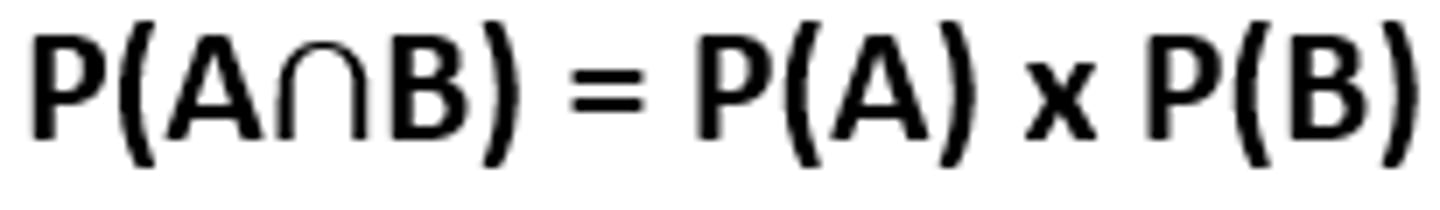
Independent Events Example

- Ex. of 2 independent events: Rolling a 3 on a die (A) and flipping a tail on a coin (B)

Since these events are independent, the joint probability of both events occurring is:

P(A∩B) = P(A) x P(B)

= 1/6 x 1/2

= 0.16 ̅ x 0.5

= 0.083 or 8.3%

Either/Or Probability

- P(AUB) is the probability that event A will occur, or event B will occur

- Key to understanding either/or probabilities is to know that the word “or” is usually involved in the question

Addition Rule - Either/Or Probability

- The Addition Rule is used to calculate either/or probabilities

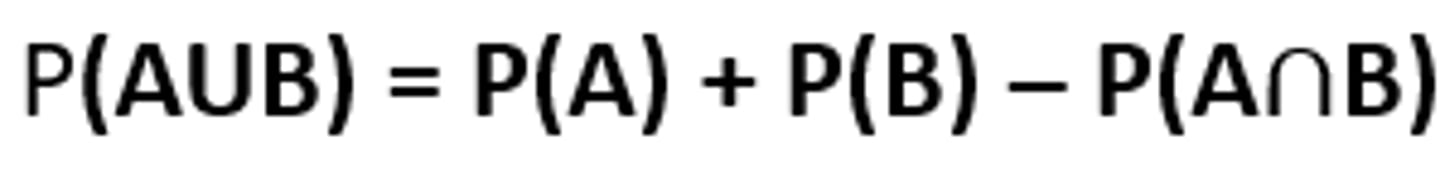
Addition Rule Example

What is the probability of:

1. Being male (M) or being a 1-19 times lifetime user (A)?

P(MUA) = P(M) + P(A) – P(M∩A)

= 75/111 + 39/111 - 32/111

= 0.739 or 73.9%

2. Being a 1-19 times lifetime user (A) or a 20-99 times lifetime user (B)?

P(AUB) = P(A) + P(B) – P(A∩B)

= P(A) + P(B)

= 39/111 + 38/111

= 0.694 or 69.4%

*No overlap between events (therefore, no subtraction)

Joint Probability - Not Mutually Exclusive

The joint probability is subtracted in the formula:

P(AUB) = P(A) + P(B) – P(A∩B)

*This corrects for the double counting that would occur if events A and B are not mutually exclusive [the probability of both A and B occurring would be included in both P(A) and P(B)]*

Joint Probability - Mutually Exclusive

If events A and B are mutually exclusive, then the either/or probability is simply the sum of the two marginal probabilities:

P(AUB) = P(A) + P(B)

Joint (and) Probabilities

- Multiplication Rule always applies: P(A) x P(B|A)

- Simplification exists if events independent: P(A) x P(B)

Either/Or Probabilities

- Addition Rule always applies: P(A) + P(B) – P(A∩B)

- Simplification exists if events mutually exclusive: P(A) + P(B)

The probability of two independent events A & B occurring is:

a) P(A) x P(B)

b) P(A) + P(B)

c) P(A) + P(B) - P(A - B)

d) P(A) + P(B) - P(A x B)

Answer = A

Probability Distributions

Discrete

- The probability distribution of a discrete random variable is a table, graph, formula, or any other device that specifies all possible values of a discrete random variable along with their corresponding probabilities

- Ex. Flipping a coin, cancer stages, Binomial distribution & Poisson distribution

Discrete Example #1

Discrete Example #2

Normal Distribution

Questions - Discrete

Normal Distribution

- The most important distribution in statistics is the normal distribution

- The normal distribution is completely determined by the parameters μ and σ

- Where π and e are the familiar constants, 3.14159 and 2.71828, respectively

It is a continuous (not discrete) probability distribution:

- We do not calculate the probability of a specific value of X (as done with discrete distributions), because the probability that X is exactly equal to a specific value is 0

- Instead, we calculate the probability that X falls within a range of values or above/below a certain value

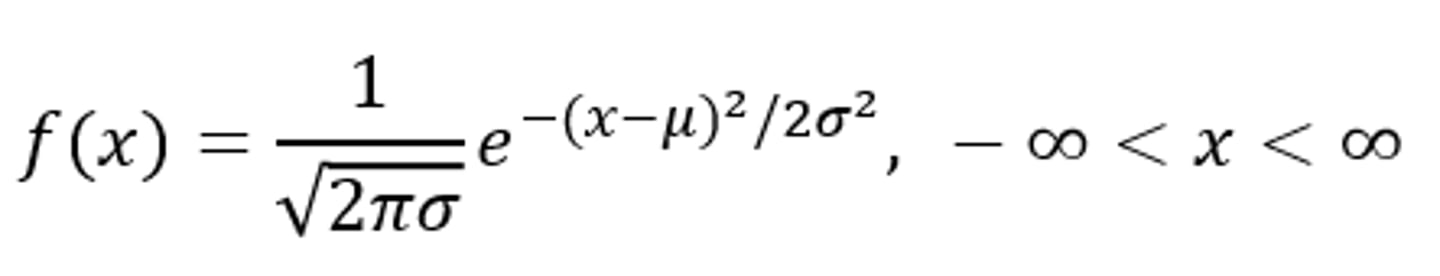
Normal Distribution Characteristic #1

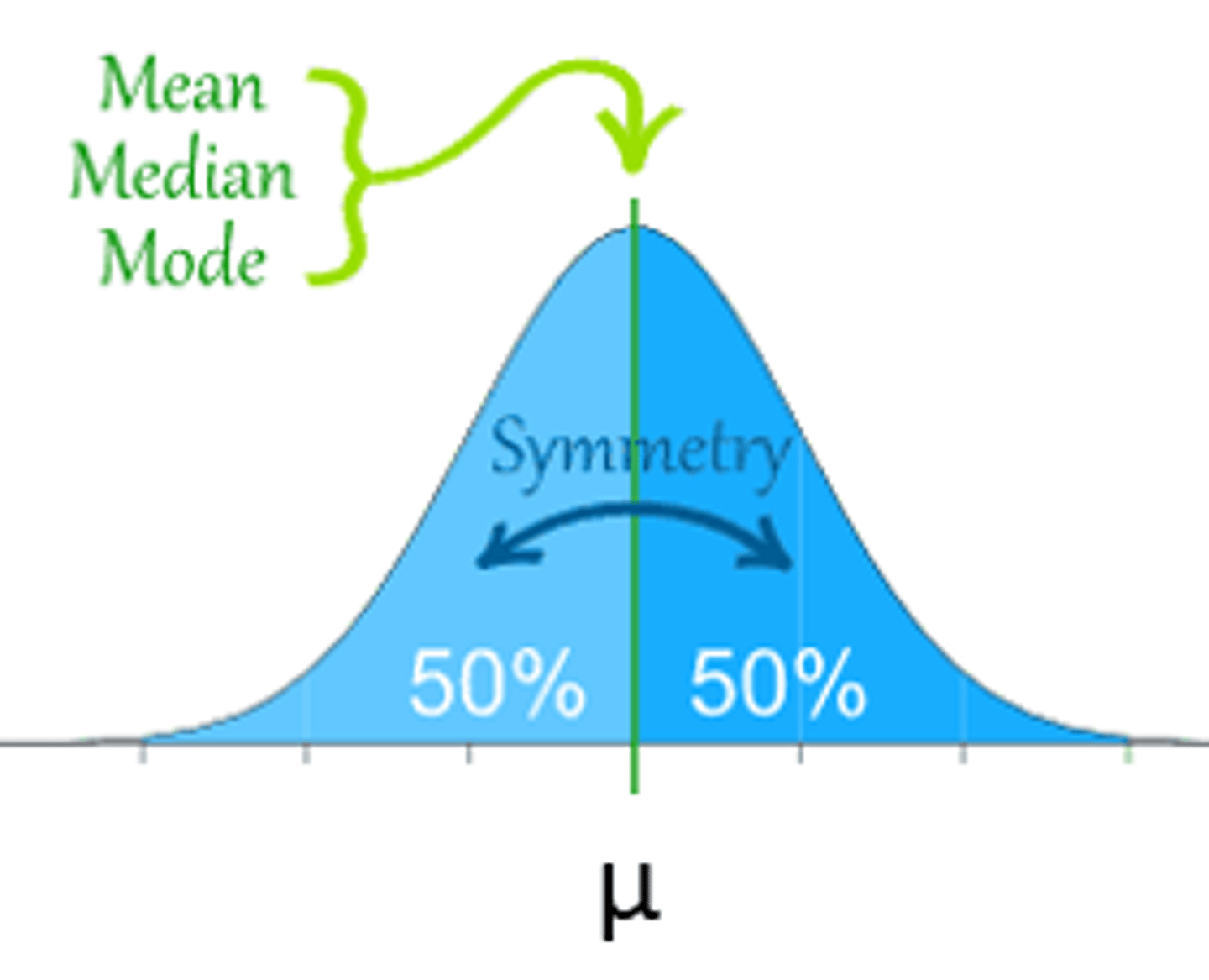
1. It is symmetrical about the mean, μ

Normal Distribution Characteristic #2

2. The mean, the median, and the mode are all equal

Normal Distribution Characteristic #3

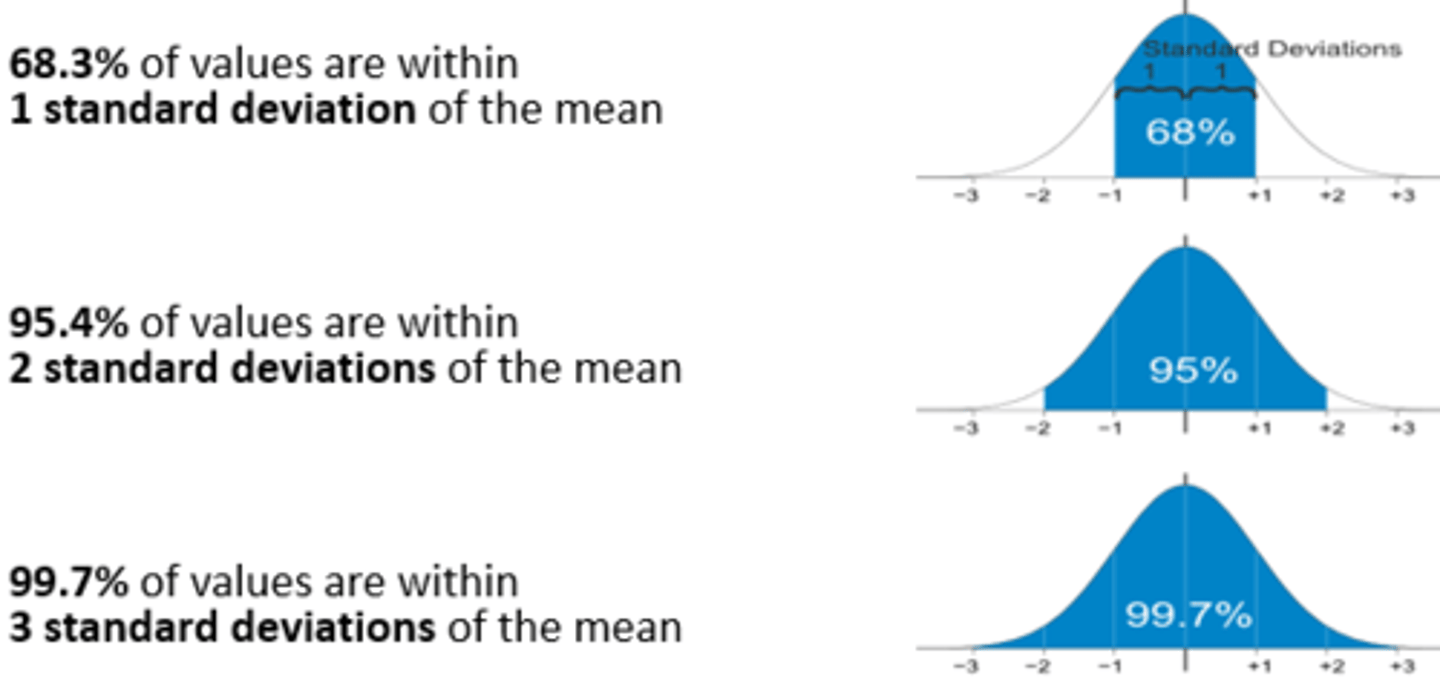
3. The percentage of values falling within 1, 2 & 3 standard deviations of the mean is known

*Usually known as normal range!

*If it is normal distribution the % will always be the same!!

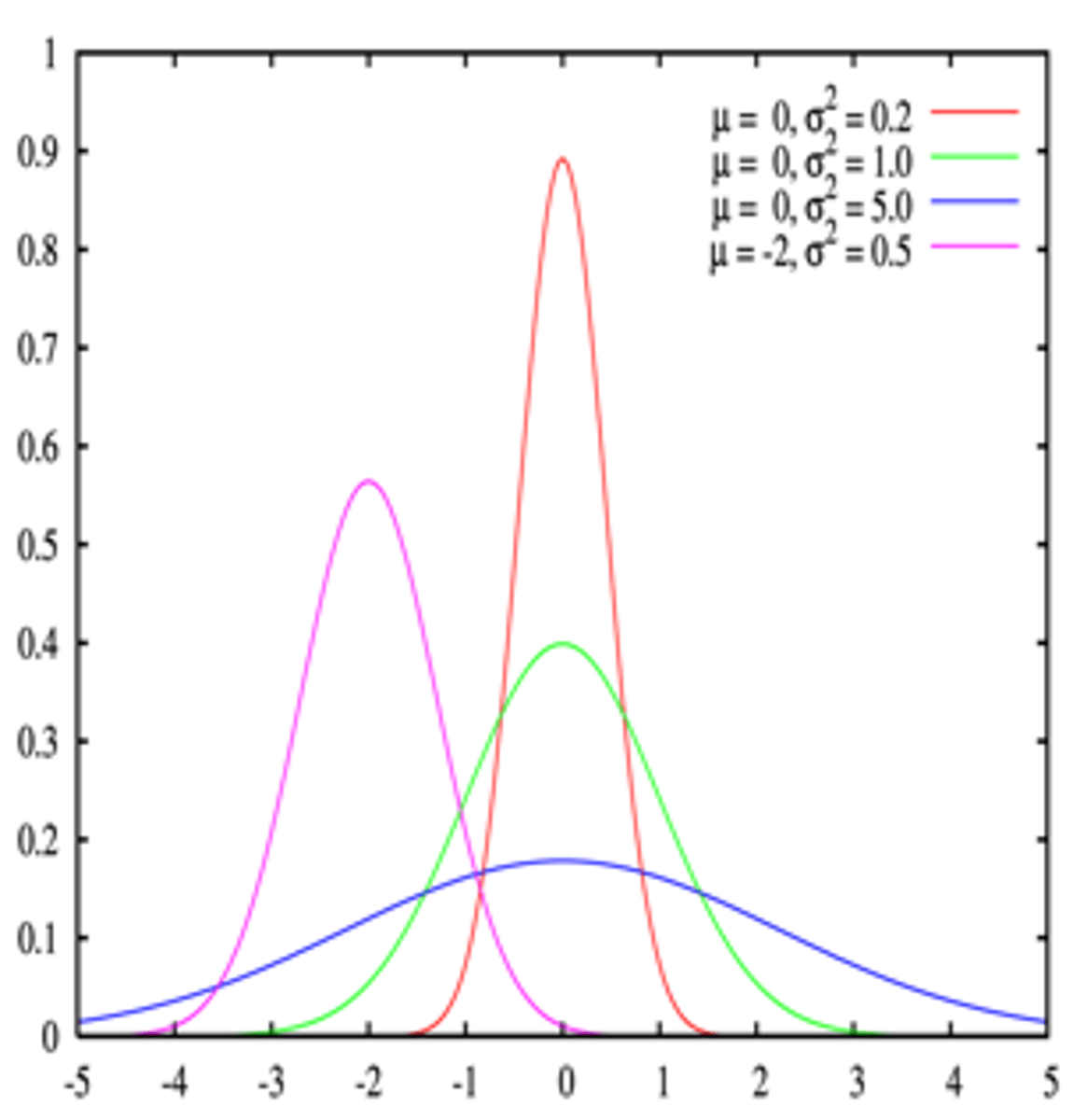
Normal Distribution - Family Example

- The Normal distribution is a family of distributions with each member distinguished from another one based on the values of μ and σ

- Variance increases = Larger tails

- Whole area under curve = 1 (no matter variance or mean)

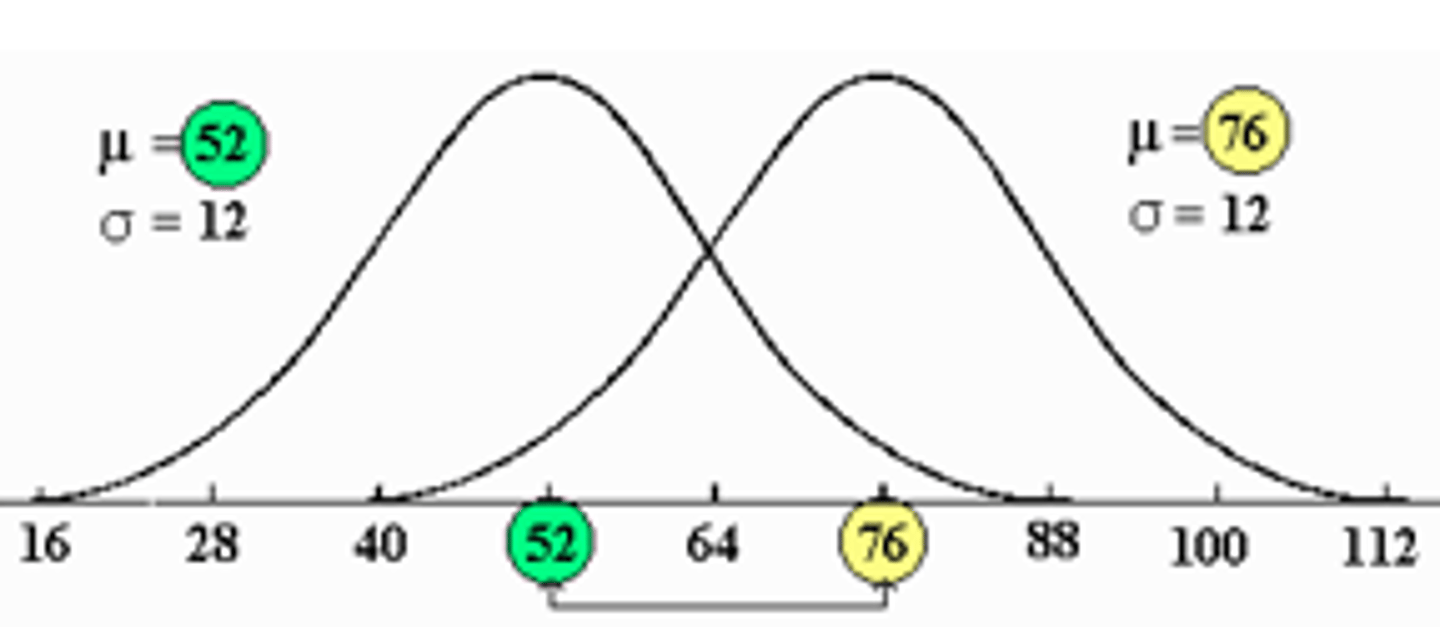
Normal Distributions with Equal Variances (SD's) & Different Means

Two normal distributions with equal variances (SD’s) and different means:

μ1 = 52, μ2 = 76

σ1 = σ2 = 12

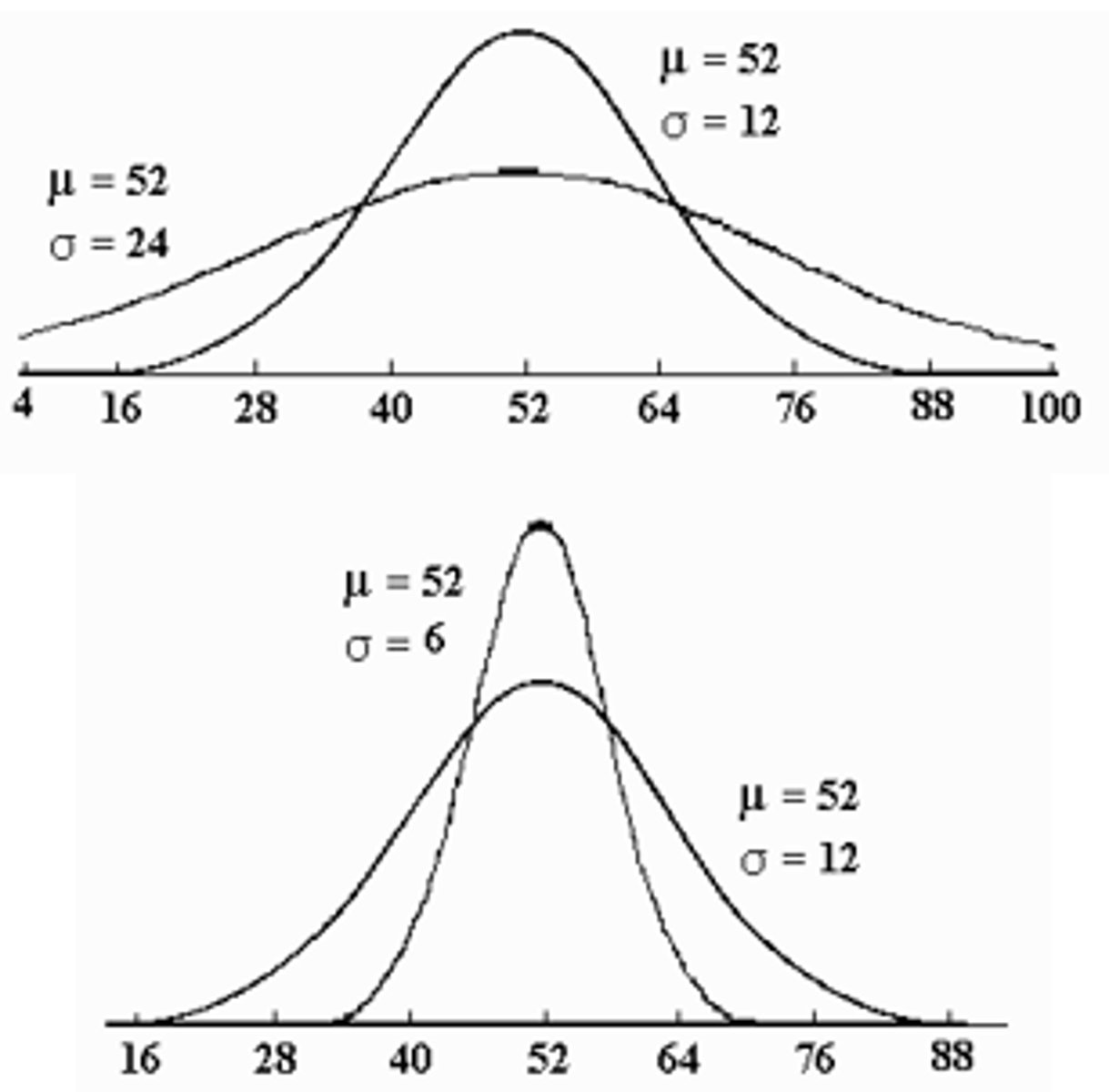
Normal Distributions with Equal Means & Different Variances (SD's)

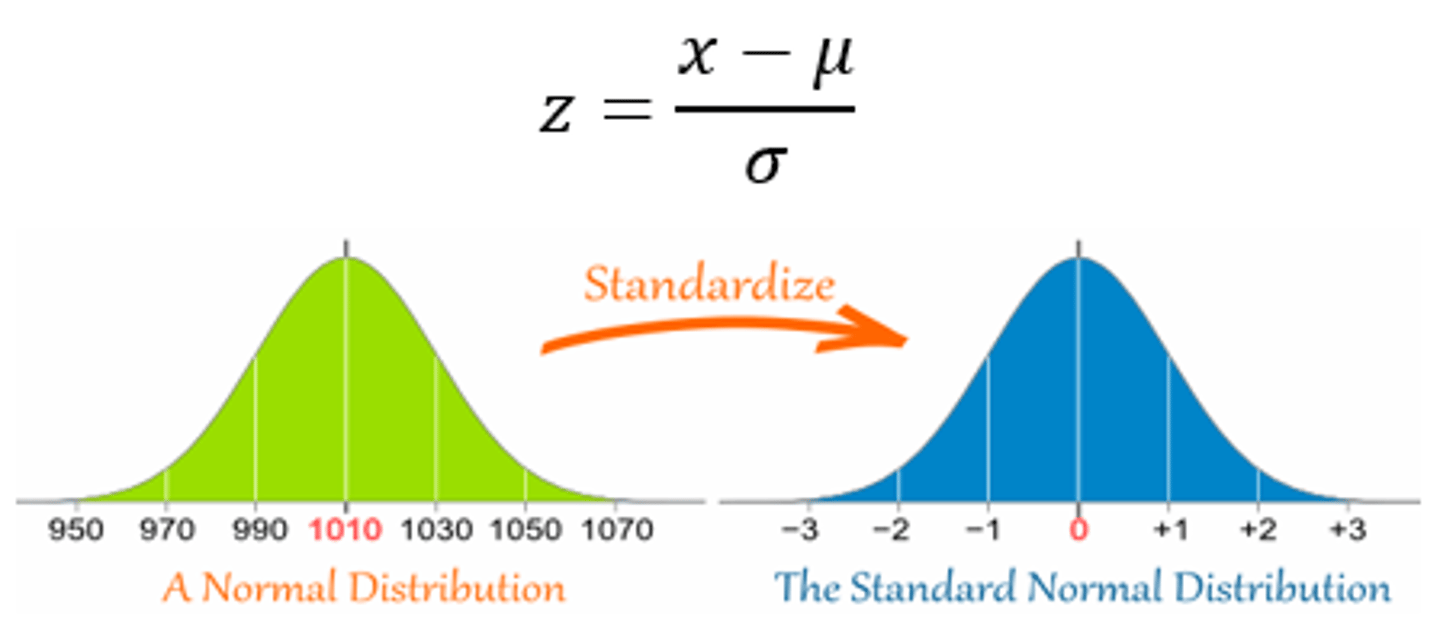
Standard Normal Distribution

- We can standardize all normal distributions, so each has mean (μ) = 0 and standard deviation (σ) = 1 by computing the z score

- This allows us to determine the probabilities of values for our original data using one probability table that has been created for the standard normal distribution

Normal Distribution -> Standard Normal Distribution

x = Any value from the graph

*Must transform ND -> SND to be able to caclulate resutls

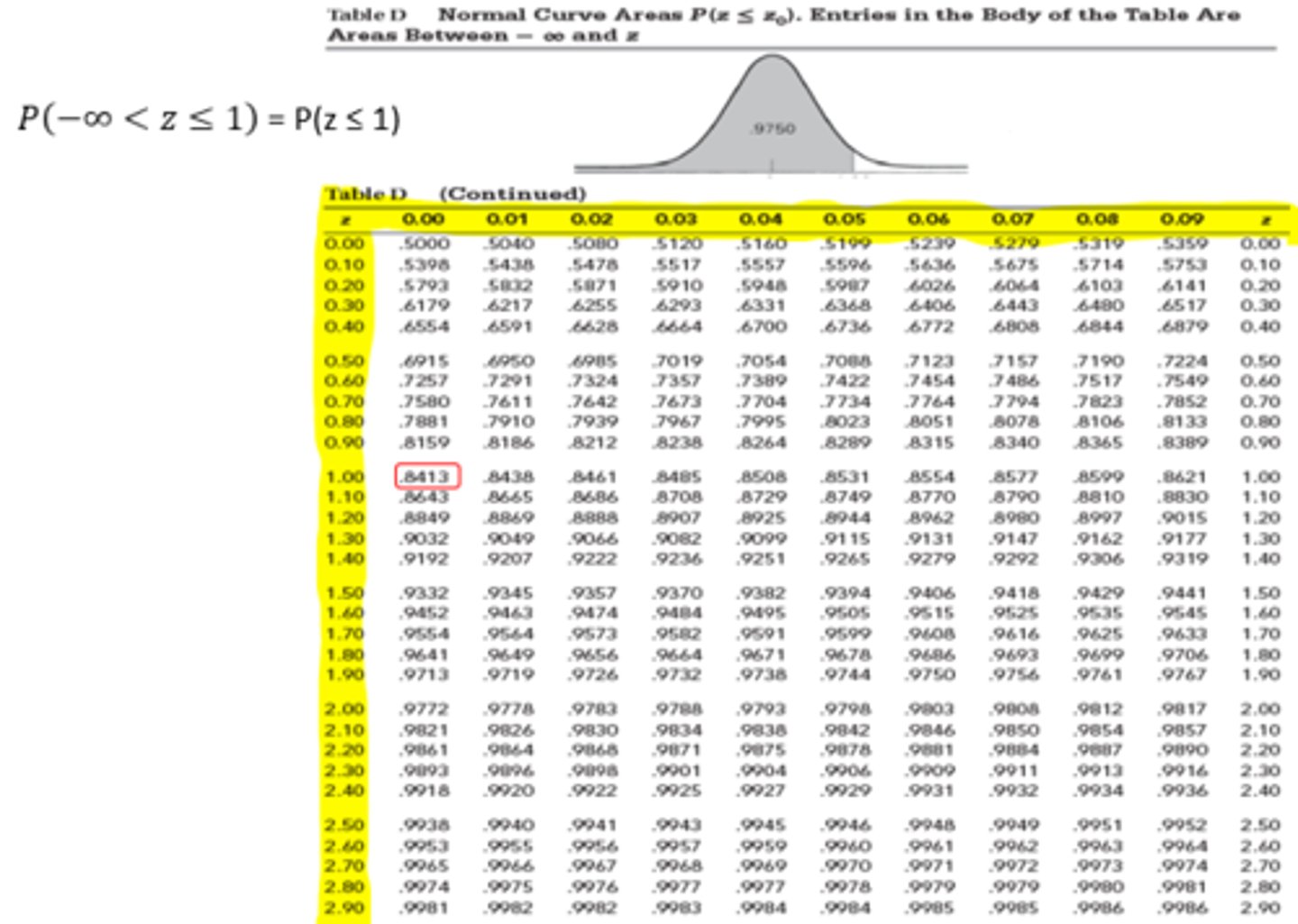
SND Values - Positive

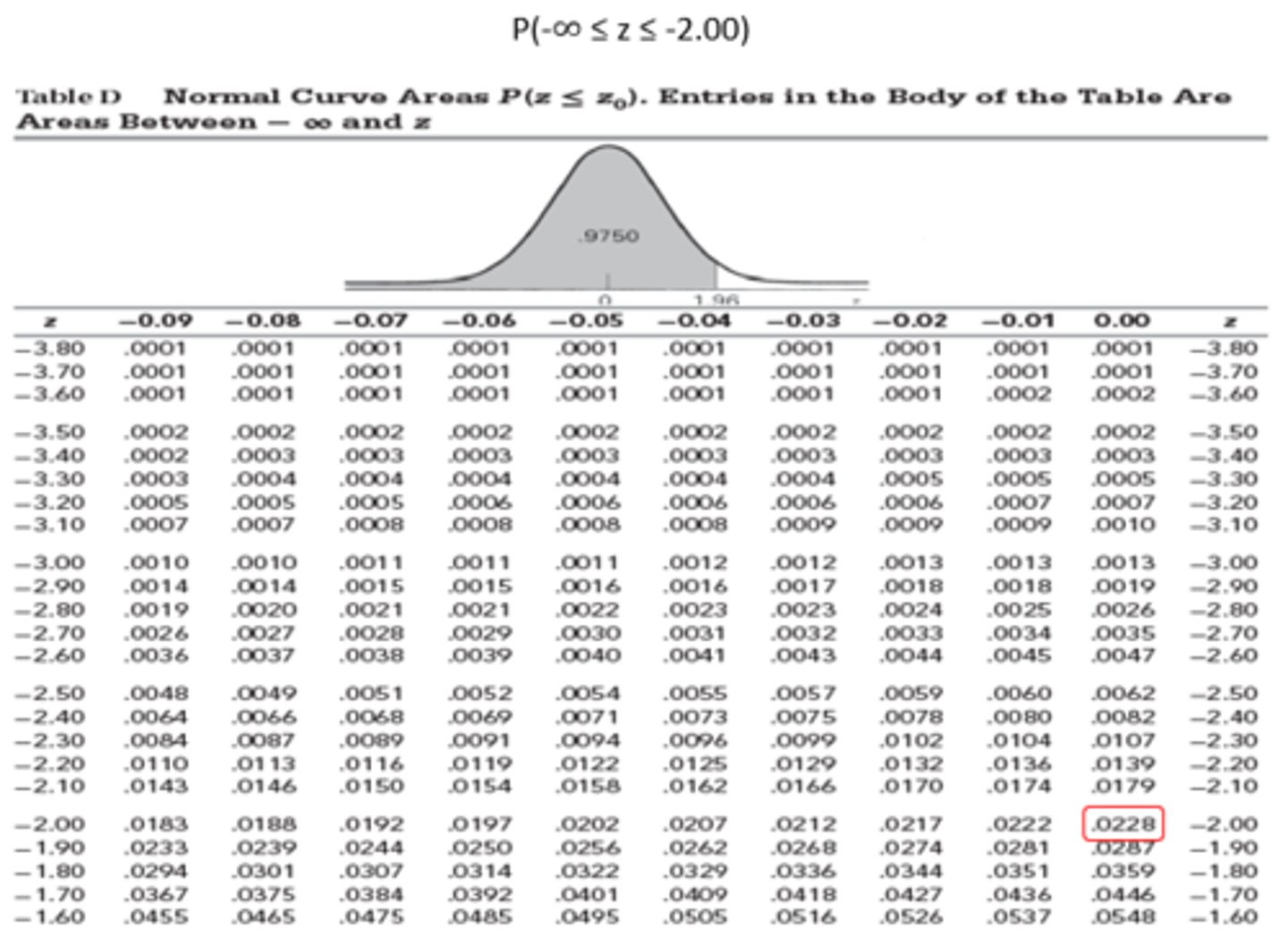
SND Values - Negative

Suppose you have a normal distribution for a random variable x, with μ = 40. The z statistic = 2 for a value of x = 80 in your distribution.

What is σ?

a) 6

b) 8.5

c) 10

d) 20

Answer = D