Module 3: 3-1: Normal Distribution pt. 1

Shifting data

adding or subtracting a constant to every value

Shifting data effects:

• Position: center, percentiles, max/min

• Shape and Spread: range, IQR, standard deviation stay the same

Rescaling data:

multiplying or dividing every value by a constant

Rescaling data effects:

• Position: center, percentiles, max/min

• Spread: range, IQR, standard deviation

• Shape stays the same

Standard deviation measures:

location of the distance to the mean to the other observations in the sample

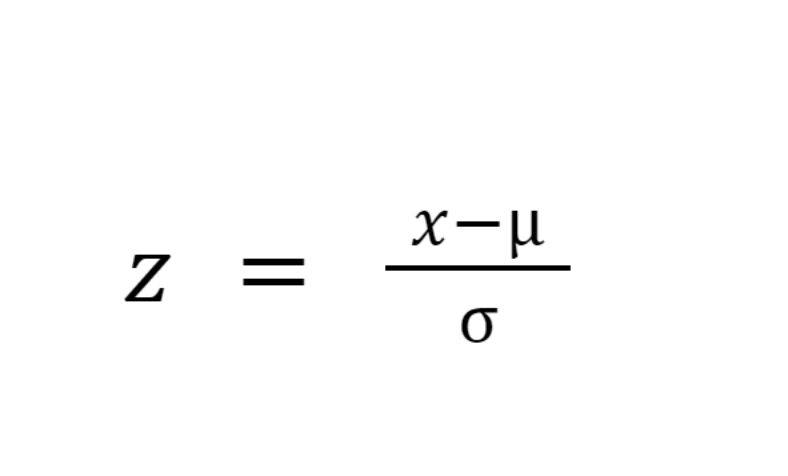
z-score (standardized value)

measure of relative standing:

• how many standard deviations away from the mean and which direction?

• can compare values measured on different scales, units, populations

Positive z-score

y is above the mean

Negative z-score

y is below the mean

z-score of 0

value is exactly on the mean

standardizing

• changes center by making the mean 0

• changes the spread by making the standard deviation 1

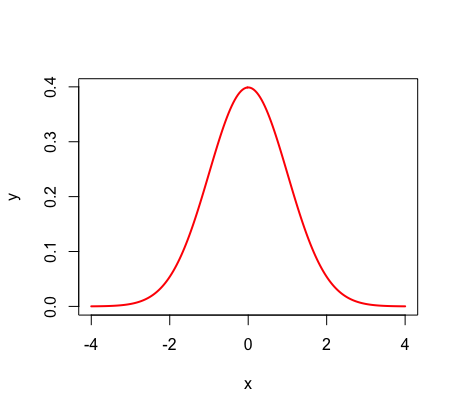
density curve

smooth curve may fit on the histogram:

density curve properties

• total area equals to 1

• area under under curve above a certain interval is the proportions of all observations falling in that range; P(a<x>b)

• no probability attached to any single value

• P(x+a)=0

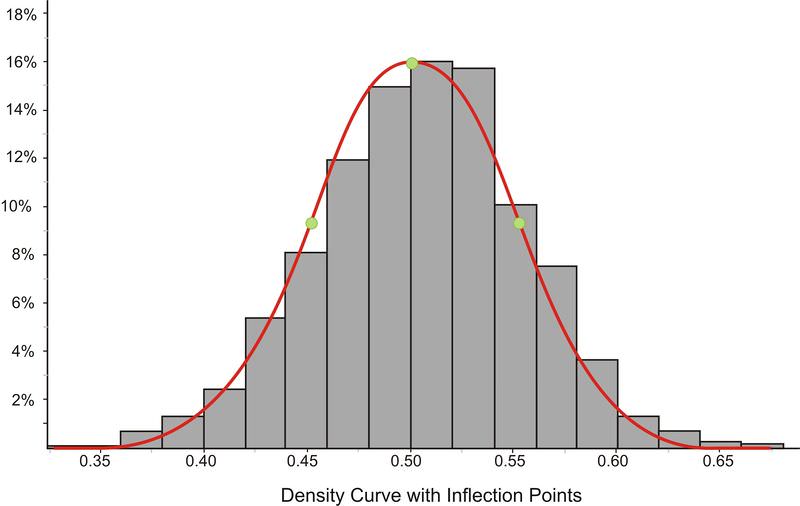
Normal Distribution

provides a reasonable approximation for modelling data and used for probability distributions

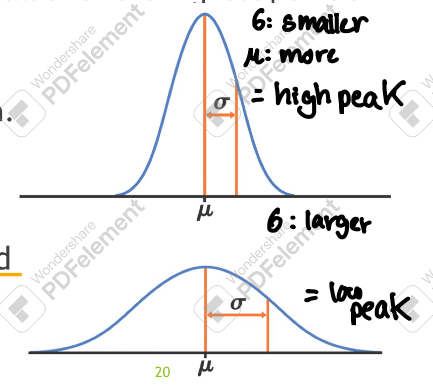
normal distribution properties

• symmetric, unimodal and bell-shaped curves

• every combination of a mean and a standard deviation, there is a different curve

normal distribution notation:

N(u,o)

standard normal distribution notation

z ~ N(0,1)