Sampling Distribution Models

The Central Limit Theorem for Sample Proportions

The sampling distribution model of the sample proportion from a random sample is approximately NORMAL for a large ‘n’

p-hat formula

p-hat = x/n where x is the number of individuals with the characteristic and n is the total number in the sample

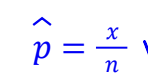
center of sampling distribution model for proportions

μ(p-hat)= p (the center of the sampling distribution of sample proportions is the true/ population proportion)

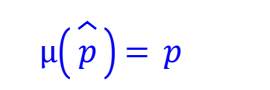
Standard Deviation of Sampling Distribution Model for proportions

SD(p-hat)= square root of (pq)/n

Assumptions and Conditions for Sampling Distribution Model for proportions

• Independence Assumption

• Sample Size Assumption

• Randomization Condition

• 10% Condition

• Success/Failure Condition

Independence Assumption

Sample values are independent

Sample Size Assumption

Samples must be “large enough”

Randomization Condition

It must come from a SRS or be results from an experiment with random assignment (not biased)

10% Condition

Must be no larger than 10% of the population

Success/Failure Condition

np ≥ 10 and nq ≥ 10

The Central Limit Theorem for Sample Means

The sampling distribution of any mean becomes more nearly Normal as the sample size grows. This is true regardless of the shape of the population distribution.

*The mean of a random sample is a random variable whose sampling distribution can be approximated with the Normal model. The larger the sample, the better the approximation will be.

Formula for center of Sample Distribution model for means

E(y-bar)= u

*population mean is not used

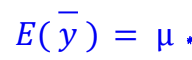
Formula for Standard Deviation of Sample Distribution model for means

SD(y-bar) = Standard Deviation of population divided by number of individuals in sample

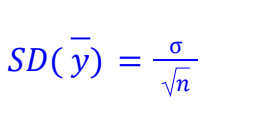
Assumptions and Conditions for Sample Distribution model for means

• Independence Assumption

• Sample Size Assumption

• Randomization Condition

• 10% Condition

• Large Enough Sample Size Condition

Large Enough Sample Size Condition

It depends on whether or not the population distribution is unimodal and symmetric. Usually we say above 30 is a good enough sample size to allow for us to use a Normal Model for the Sample Distribution model for means

What can go wrong?

• Dont confuse sampling distribution of a statistic with distribution of a sample (sample data could be highly skewed but sampling distribution can be normal)

• Larger sample = more sampling distribution of proportions/means look like population

• Beware of observations that are not independent

• Can’t use CLT for small skewed samples