Quick Sort

Divide and Conquer in Merge Sort

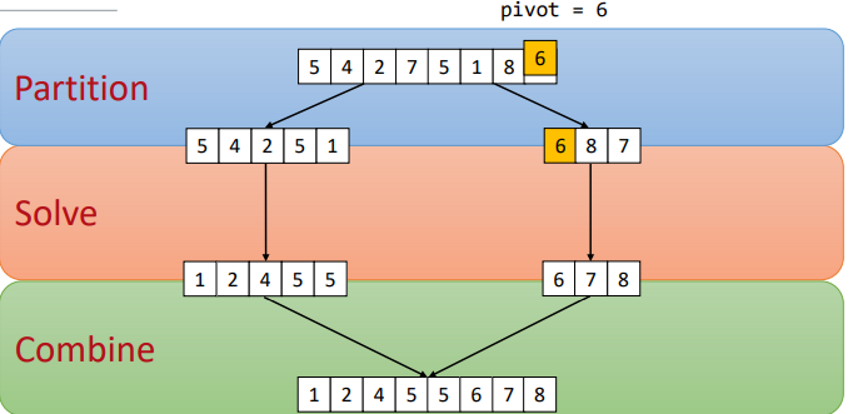
• Partition: Partition the input array according to a pivot

  • One sub-array contains all elements smaller than the pivot

  • The other contains all elements greater than the pivot

• Solve: Recursively solve (i.e., sort) the two subarrays independently

• Combine: Combine the two sorted subarrays by (simple) merging to get an overall sorted array

Split, Solve, Combine

Code

class QuickSort {
   static void quickSort(int array[]) {
      resursiveQuickSort(array, 0, array.length - 1);
   }

   ststic void recursiveQuickSort(int array[], int low, int high) {
      if (low < high) {
         int p = partition(array, low, high);
         recursiveQuickSort(array, low, p - 1);
         recursiveQuickSort(array, p + 1, high);
      }
   }

   static int partition(int array[], int low, int high) {
      int pivot = array[high];
      int i = low;
      for (int j = low; j < high; j++) {
         int tmp = array[i];
         array[i] = array[high];
         array[high] = tmp;
         return i;
      }
   }
}

Correctness

for inputs of size ≤ n

• Prove by (strong) induction that Correctness(n) is true for all 𝑛 ≥ 1

• Base step (for 𝑛 = 1): 

  • Correctness(1) is clearly true, as an array with one entry is already sorted

• Induction step (for 𝑛 > 1): 

  • First, assume that the induction hypothesis holds for all integers 𝑛′ ≥ 1, 𝑛′ < 𝑛

  • Recall that Quick Sort splits an input array of size 𝑛 into two smaller arrays of size n1, n2 < 𝑛, and then recursively runs Quick Sort on each smaller array

  • The induction hypothesis holds for 𝑛1 and 𝑛2, and thus these recursive calls return sorted arrays

  • Finally, the two smaller, sorted arrays combine into the sorted version of the input array (of size 𝑛). This completes the induction step

Worst-Case Time Complexity

Cost of Operations: 

• Partitioning an array of size 𝑘 takes 𝑐1𝑘 elementary operations.

• Combining two sorted arrays from the recursive calls takes 𝑐2 elementary operations

Time Complexity: 

• 𝑇𝑄(𝑛) is the time complexity of Quick Sort when run on an input of size 𝑛

• Quicksort takes the most time when the recursive calls are unbalanced: one of the recursive calls is done on an array of size 𝑛 − 1 

  • 𝑇𝑄(𝑛) ≤ 𝑇𝑄(𝑛 − 1) + 𝑇𝑄(0) + 𝑐1 ⋅ 𝑛 + 𝑐2 

  • Repeating this, we get: 𝑇𝑄(𝑛) ≤ 𝑛 𝑇Q(0) + 𝑐1 ⋅ 𝑛2 + 𝑐2 ⋅ 𝑛

  • From which you can show that: 𝑇𝑄(𝑛) = 𝑂(𝑛^2)

Analysis Summary

• Best case - O(nlog(n))

• Average case -  O(nlog(n))

• Worst case -  O(n^2)

• In-place - yes