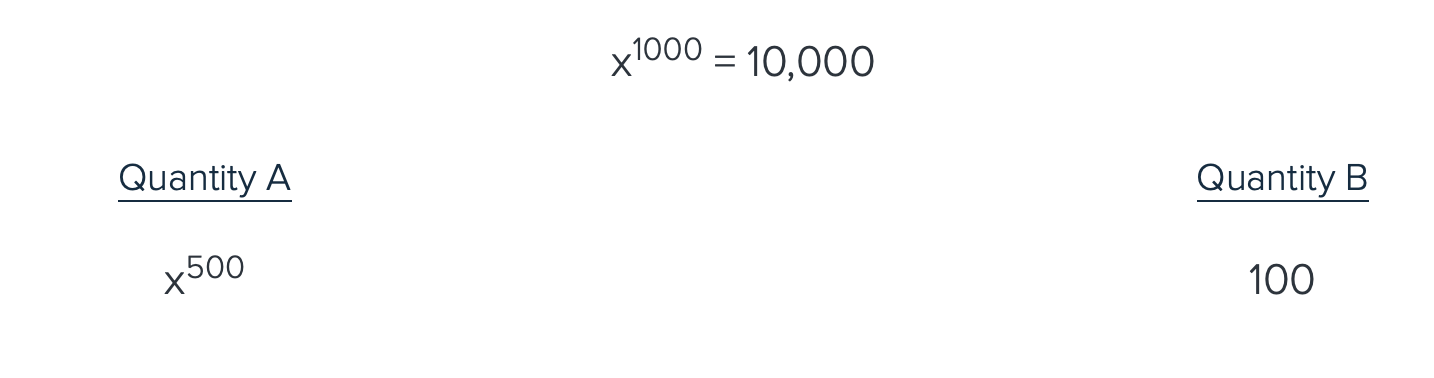Chapter 5 - Roots and Exponents

√(x² + y²) = ?

≠ x + y

bc √(x² + y²) ≠ √x +√ y

When the radical symbol (√) is used, we only consider…

the non-negative square root of the number

for example:

√100 = 10 but √100 ≠ ± 100

√25 = 5 but √25 ≠ ± 5

What is √900?

Just 30! we only consider the positive number so -30 is disregarded

The square root of a variable squared is equal to…

the absolute value of that variable. in other words, √x² = |x|

What is the difference between √81? and √x² = √81?

• √81 can only be 9

• √x² = √81

  • |x| = 9

  • x = ±9

If n = √64, then n could be equal to which of the following: -8, 4, 8? Indicate all numbers

8

when the (√) symbol is used, we only consider the non-negative square root

What is the value of √200 + √500?

√200 + √50

(√25)(√4)(√2) + (√25)(√2)

(5)(2)(√2) +(5)(√2)

10√2 + 5√2

15√2

√5 x √8

√5 × √8 → √40 → 2√10

√100 x ³√27

these don’t have the same index so you can directly multiply them together. you can simplify each radical and combine them:

√100 x ³√27 → 10 × 3 = 30

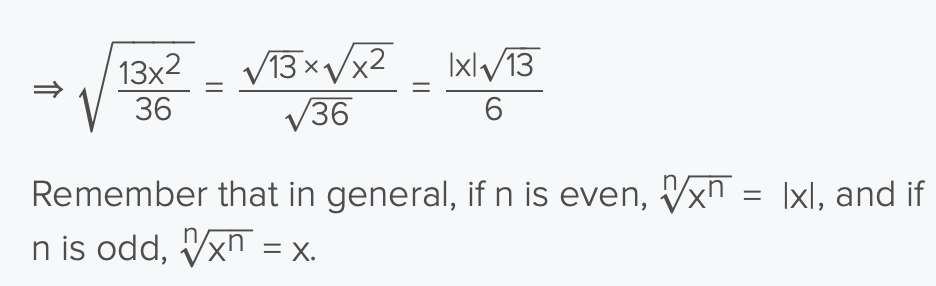
if n is even then, ⁿ√xⁿ

|x|

x will only be positive

if n is odd then, ⁿ√xⁿ

x

If x, y and m are positive, then x > y if and only if…

if and only if xⁿ > yⁿ

How to multiply radical expressions that combine radicals and non-radicals?

ex: 2√10 × 4√7

1. multiply the non-radicals with the non-radicals

   • (2)(4) → 8

2. multiply the radicals with the radicals

   • √10√7 → √70

3. combine: 8√70

2√10 × 5√2

10√20 → 10√4√5 → 10(2)√5 → 20√5

• QA: (√x + √y)² → x+ 2√(xy) +y

• QB: [√(x + y)²]² → x + y

• compare QA and QB

  • is x+ 2√(xy) +y > x + y ?

    • 2√(xy) > 0?

    • yes bc x and y are both positive

• QA is bigger

When dealing with addition and subtraction of radicals, what is the order of operations?

You must perform any addition or subtraction before taking the square

• √(a + b) ≠ √a + √b

  • √(25 + 16) ≠ √25 + √16

  • √41 ≠ 9

• √(a-b) ≠ √a - √b

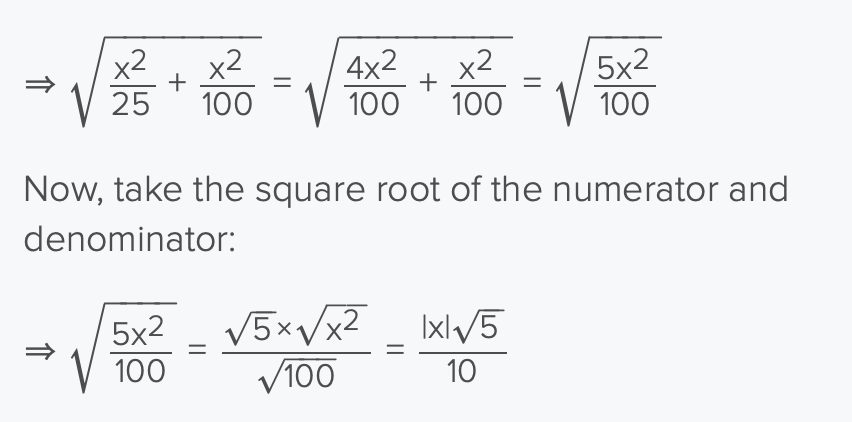
In order to add and subtract radicals, they must be…

• like radicals ~ radicals with the same root index and the same radicand (expression under the radical)

• for example,

  • you can add 5√4 + 4√4

  • you can’t add these 9√4 + 4√9

    • root 4 and root 9 are not like radicals

If n² = 625 and m³ = -125, then m+n could equal which of the following: -30, -20, or 20?

-30, 20

√(x+y)² =

|x + y|

Find x

√(x + 5)² = √36

|x + 5| = 6

• (x+ 5) = 6 → x = 6 - 5 → 1

• -(x+ 5) = 6 → -x - 5 = 6 → -x = 11 → -11

What happens when you take the square root of a squared binomial?

You need to use the absolute value signs about the expression

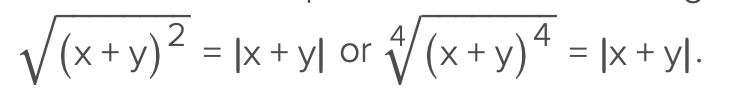
Before squaring both sides of the of a square root expression, what do you need to do?

You need to isolate the square root before squaring both sides

Ehn solving square root equations, how do you finish the problem?

If you square both sides of the equation, then you need to check each solution to eliminate extraneous solutions

If a ≠ 0, a ≠ 1, and a ≠ -1, and a^x = a^y, then …

x = y

If a ≠ 0, a ≠ 1, and a ≠ -1, and a^x + a^y = a^z, then …

x + y = z

the relationship can’t be determined

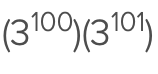
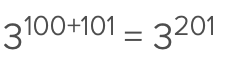
How to multiply like bases? What do you do with the exponents?

You add the exponents (as long as you have like bases)

(xⁿ)(yⁿ)

(xy)ⁿ

(2⁴)(3⁴)

6⁴

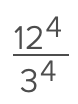
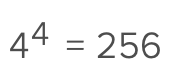
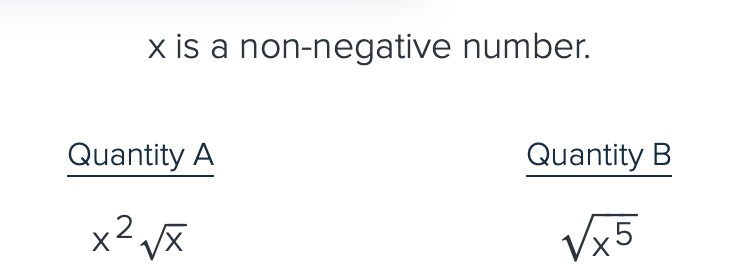
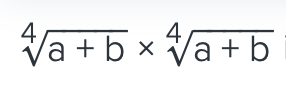
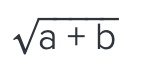
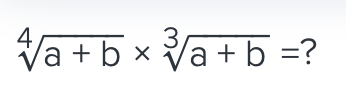
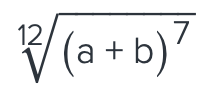
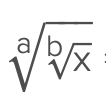
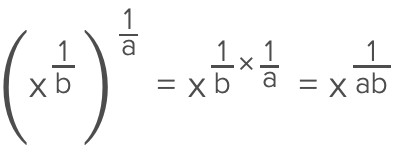
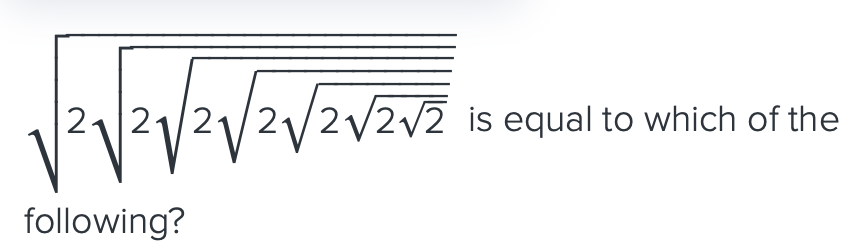
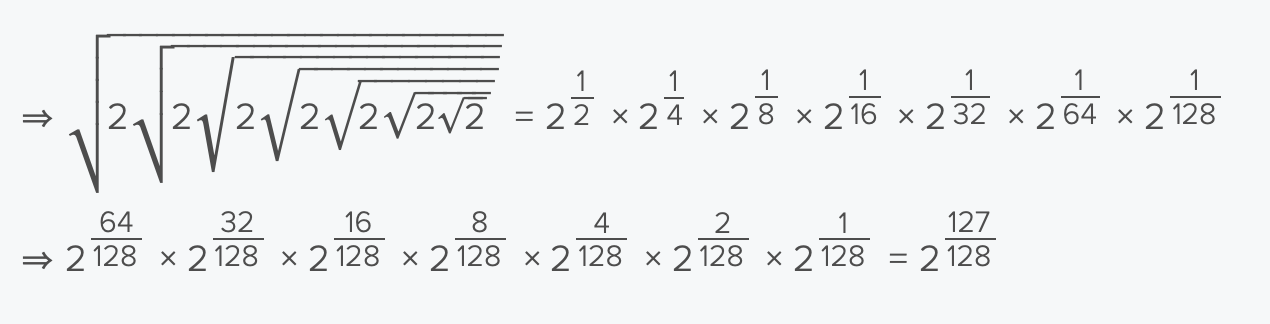
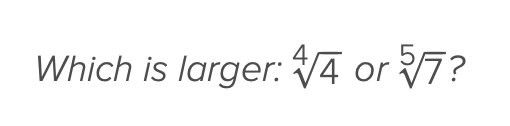
when comparing these type of numbers, it helps to raise the exponent to the Lcm

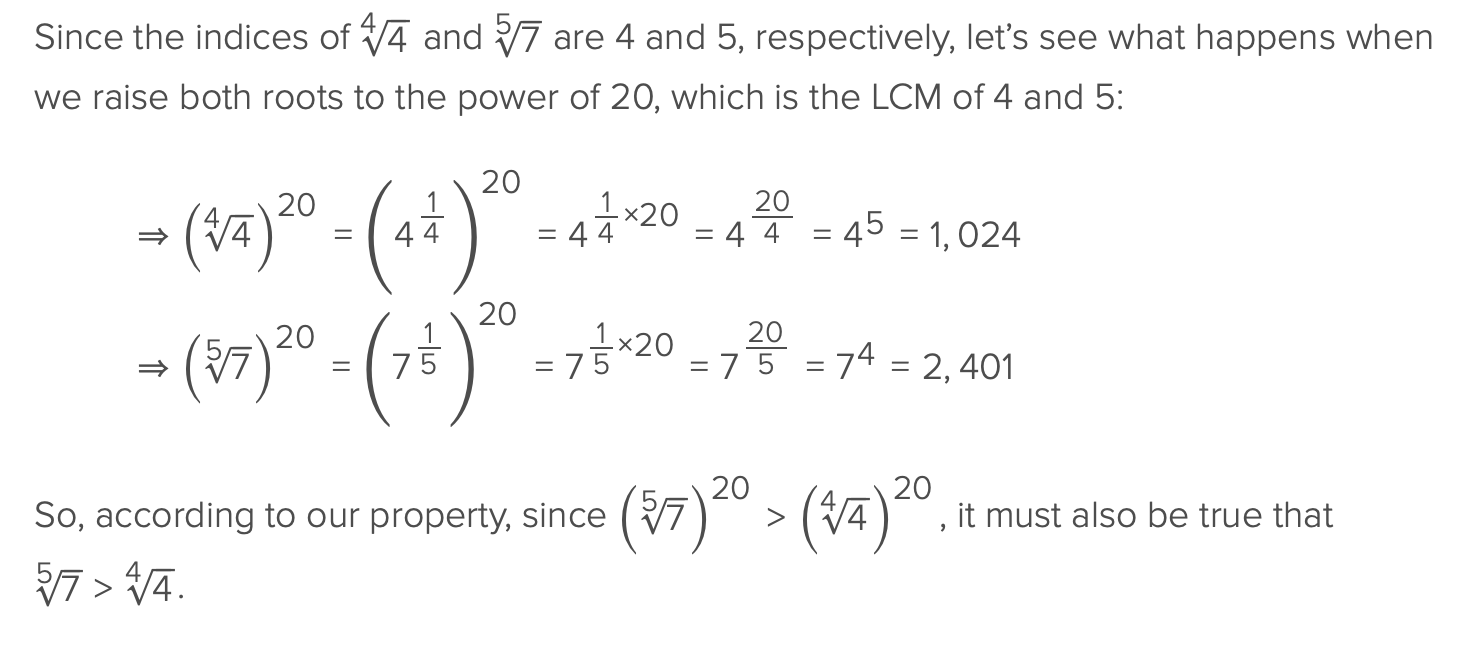
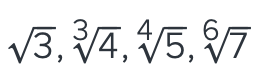
Rank these numbers in increasing order from left to right?

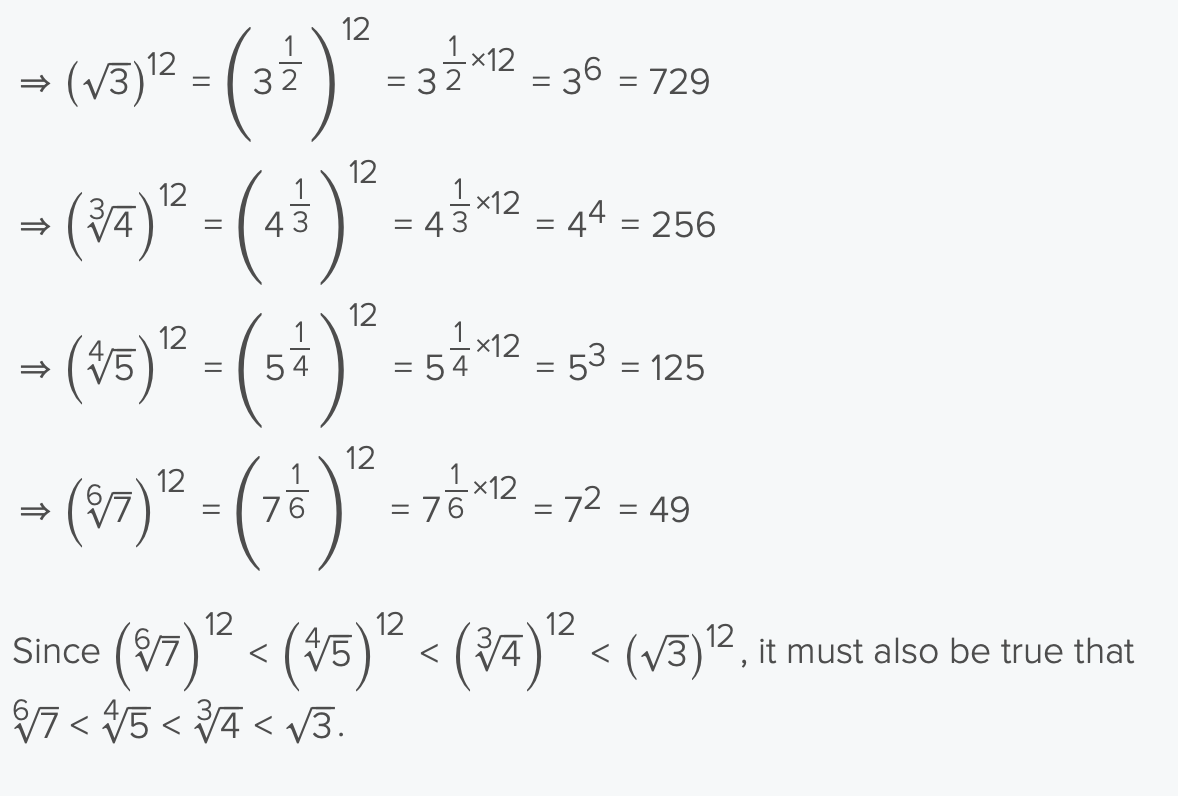
How do you compete fractions with different exponent values?

Try to make the exponents smaller by raising all values to a power of (1/GCF)

• for example rank in descending order

  • 3¹⁰⁰, 4⁷⁵, 5⁵⁰, 6²⁵

  • divide each exponent by 35

  • 3⁴, 4³, 5², 6 → rest if example in screenshot

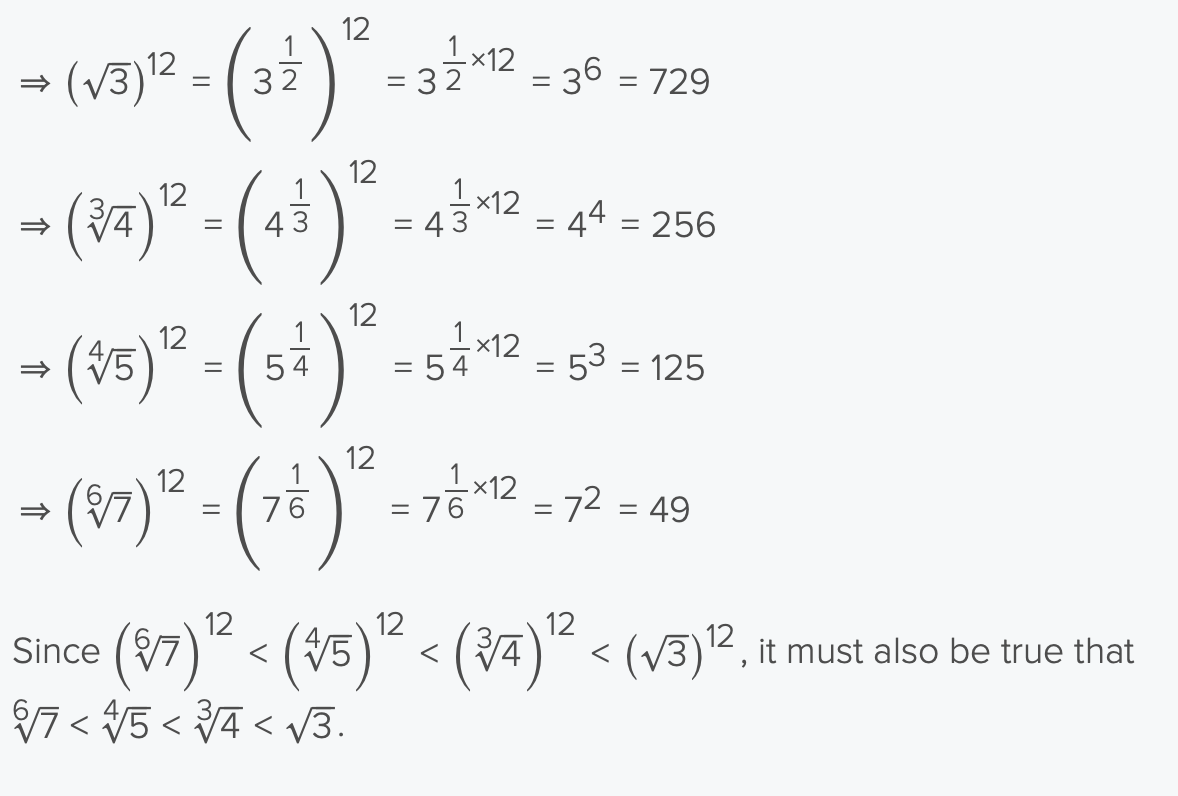
If x ≠ 0, then x⁰ =

1

5ⁿ - 5ⁿ⁻¹ = 500, what is the value of (x-1)²

9

You can’t add expressions radicals together. You can only add exponents of those expressions when you multiply them together. What’s another way to solve them?

Factor out all common factors to simplify

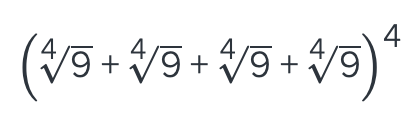
How do you add like bases with the same exponent (ex: 3⁴ + 3⁴ + 3⁴)?

use shortcut

if you know: 3⁴ + 3⁴ + 3⁴ → 3⁴(1+1+1) → 3⁵ then you can apply the formula 3ⁿ + 3ⁿ + 3ⁿ = 3ⁿ⁺¹

more examples:

2ⁿ + 2ⁿ = 2ⁿ⁺¹ → 2⁶ + 2⁶ = 2⁷

4⁵⁰ + 4⁵⁰ + 4⁵⁰ + 4⁵⁰ = 4⁵¹

provide example with shortcut

How'd do you compare fractions with exponents in denominator?

Convert all fractions to a lowest common denominator by multiplying the bases by their respective higher powers

If x is a positive fraction between 1 and 0, then what do you know about the sizes of x, x², √x?

then it must be true that:

x² < x < √x

x² is the smallest

√x is biggest

What do you need to know if you want to use exponents to estimate a number?

When comparing 2 numbers and one number has a much bigger base, especially when the exponents are relatively large, one of the numbers might be significantly bigger

10⁷