AQA A-Level Physics PAPER 2

Can you define internal energy?

= the sum of the random distribution of the kinetic and potential energies of the object's molecules

When does molecular kinetic energy increase?

When does potential energy increase?

When does internal energy increase?

molecular kinetic energy increases as temperature increases

potential increases if object changes from solid to liquid or liquid to gas

internal increases if work is done (potential) or if the temperature is increased (molecular KE)

What is thermal equilibrium?

two objects are said to be in thermal equilibrium when there is no net transfer of heat energy between them

this will only occur if both objects are at the same temperature

What is the zero law of thermodynamics?

if A is in thermal equilibrium with B, B is in thermal equilibrium with C...

then A is in thermal equilibrium with C

What is the first law of thermodynamics?

the internal energy of a system can only change by exchanging energy with its surroundings, either by doing work or by heating

ΔU = ΔQ + ΔW, where ΔU internal is change in internal energy, Q is heat absorbed and W is work done.

What is the second law of thermodynamics?

thermal energy moves from regions of higher to lower temperature

What is the lowest temperature possible?

absolute zero.

0K or -273.15℃

an object at absolute zero has zero internal energy

What is the third law of thermodynamics?

absolute zero cannot be reached, and so internal energy cannot be zero

Can you define and measure specific heat capacity?

energy required to raise the temperature of 1kg of a substance by 1 degree

high SHC: heats and cools slowy

low SHC: heats and cools quickly

Can you define latent heat?

energy required to change the state of 1kg of a mass without any change of temperature

SLH of fusion (melting)

SLH of vaporisation (boiling)

SLH fusion << SLH vaporisation, must completely separate molecules so there are no forces of attraction

Can you measure latent heat?

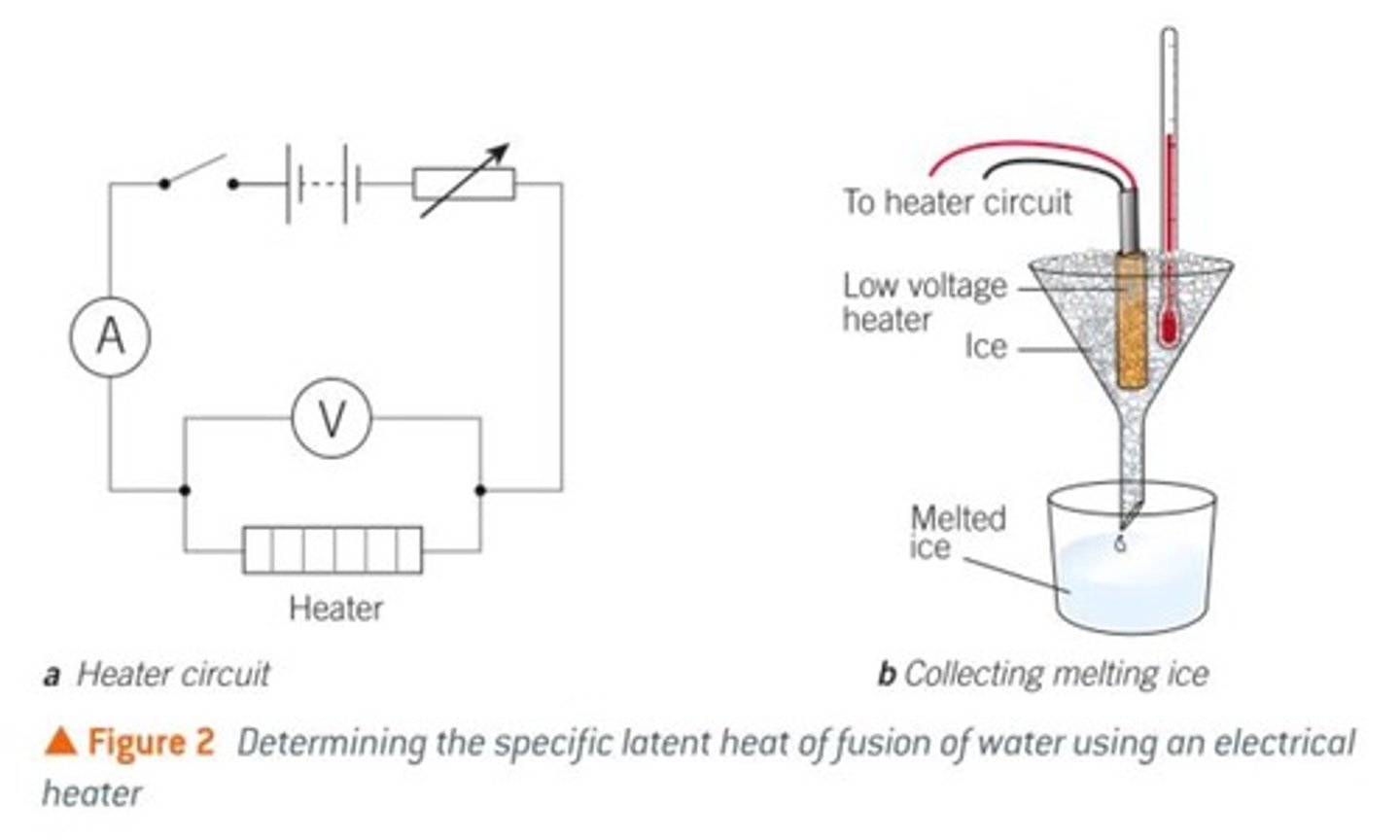
Can you explain why the temperature of a substance stays steady when it is changing state?

energy is used to break bonds between molecules for phase change to occur, not increase KE

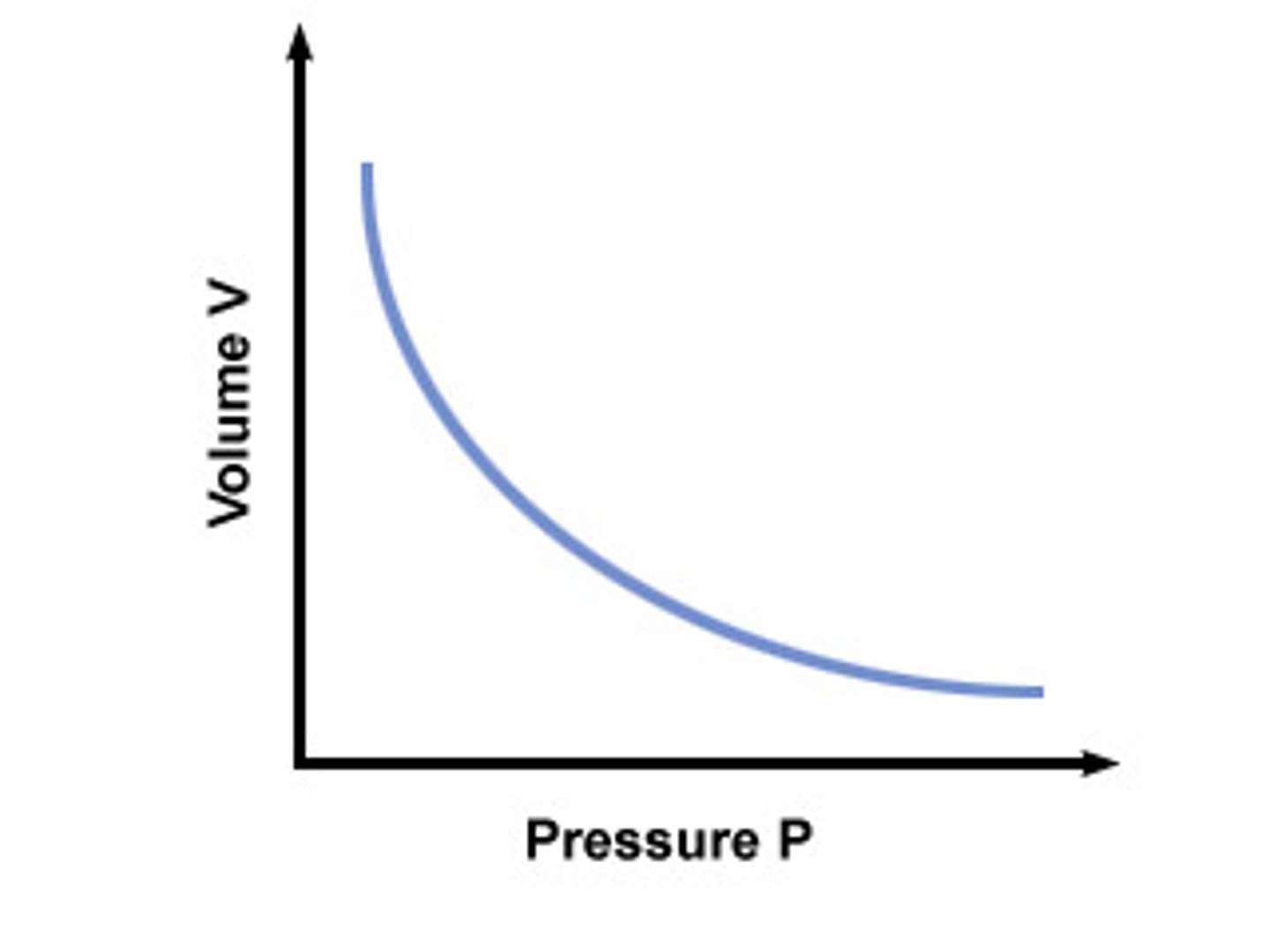
Boyle's law

P1V1=P2V2

pressure and volume are inversely related when temperature is constant

V decreases, more particles / unit volume => more collisions => higher force => higher pressure

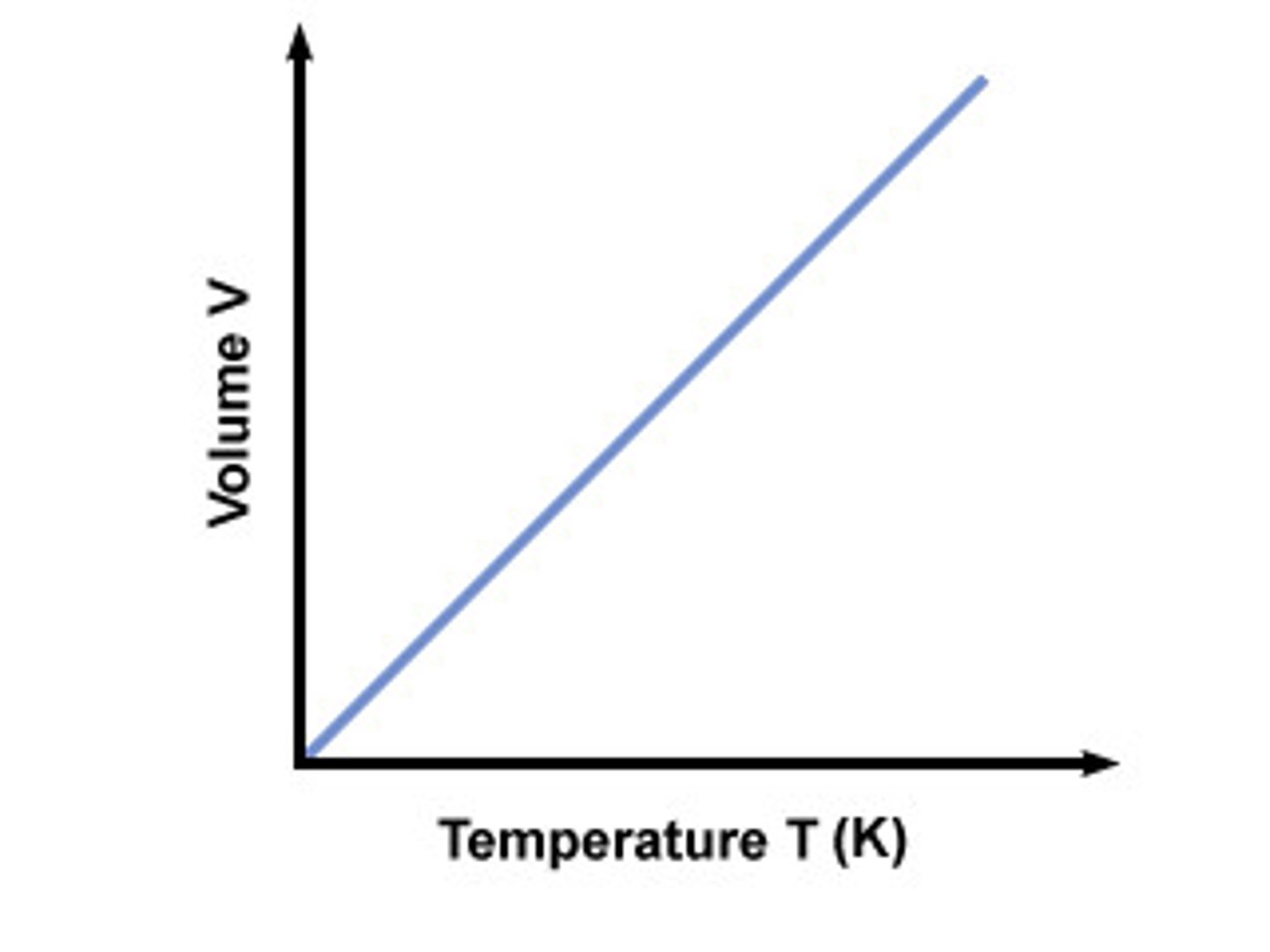
Charles' law

V1/T1=V2/T2

volume proportional to temperature, pressure constant

temperature increases => KE increases => particles can move further and faster

Pressure law

P1/T1 = P2/T2

pressure proportional to temperature, volume constant

temp increases => KE increases => more frequent collisions => higher force, same SA => higher pressure

Gas laws

experimental relationship between P, V, T

fixed mass of gas

empirical in nature (come from experimental evidence)

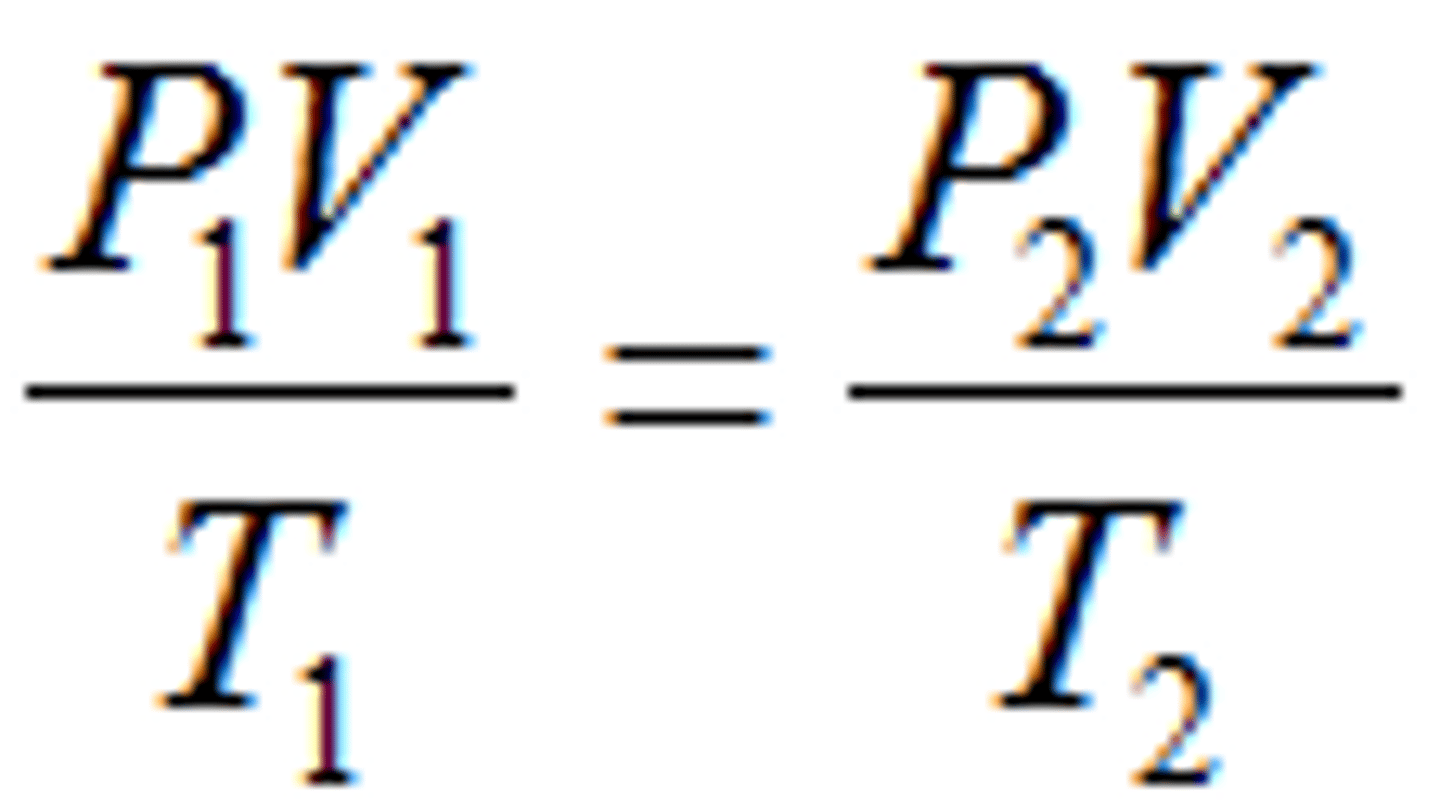
Ideal gas equation (moles)

gas laws combine to pV/T = k

k dependent on moles of gas => pV/T = nR

where n is number of moles, R is molar gas constant

Avogadro's number

number of representative particles in a mole

6.02 x 10^23

Ideal gas equation (molecules)

use pV = nRT with avogadro's number

k = R / AN => Boltzmann constant

Molar mass

the mass of one mole of a pure substance in grams

mass = mr (relative molecular mass) x mol

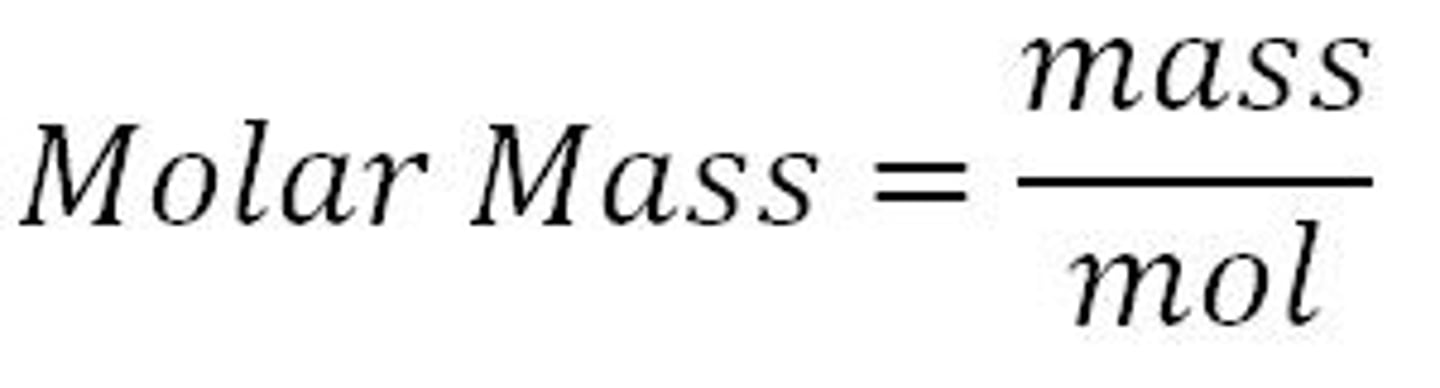
Relative molecular mass

= mass of a single molecule of a compound

sum of the relative atomic masses of the atoms presents within the compound

Work done on a gas

work is done on a gas to change its volume when at constant pressure

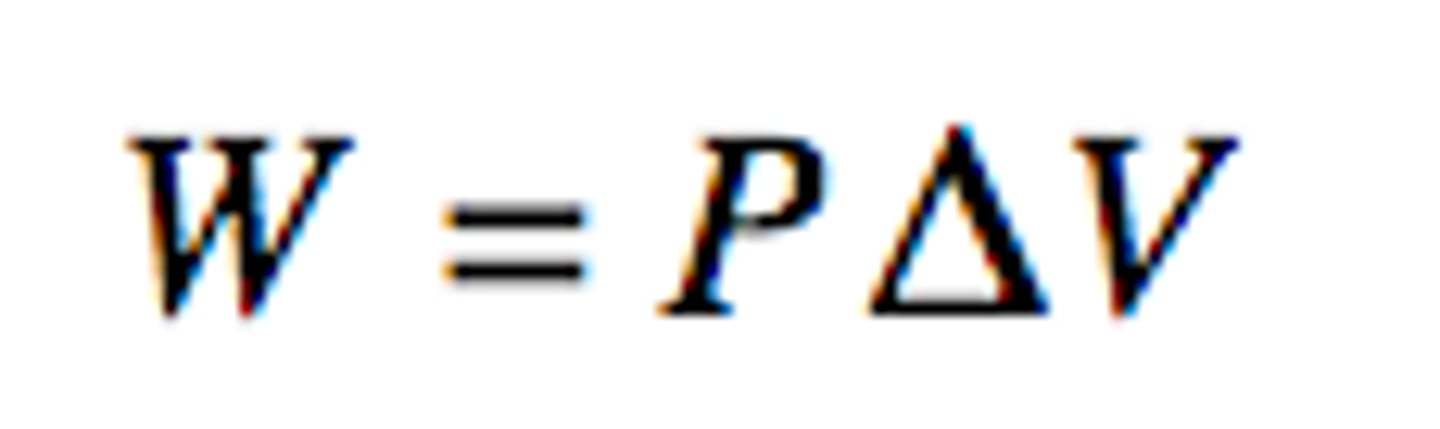
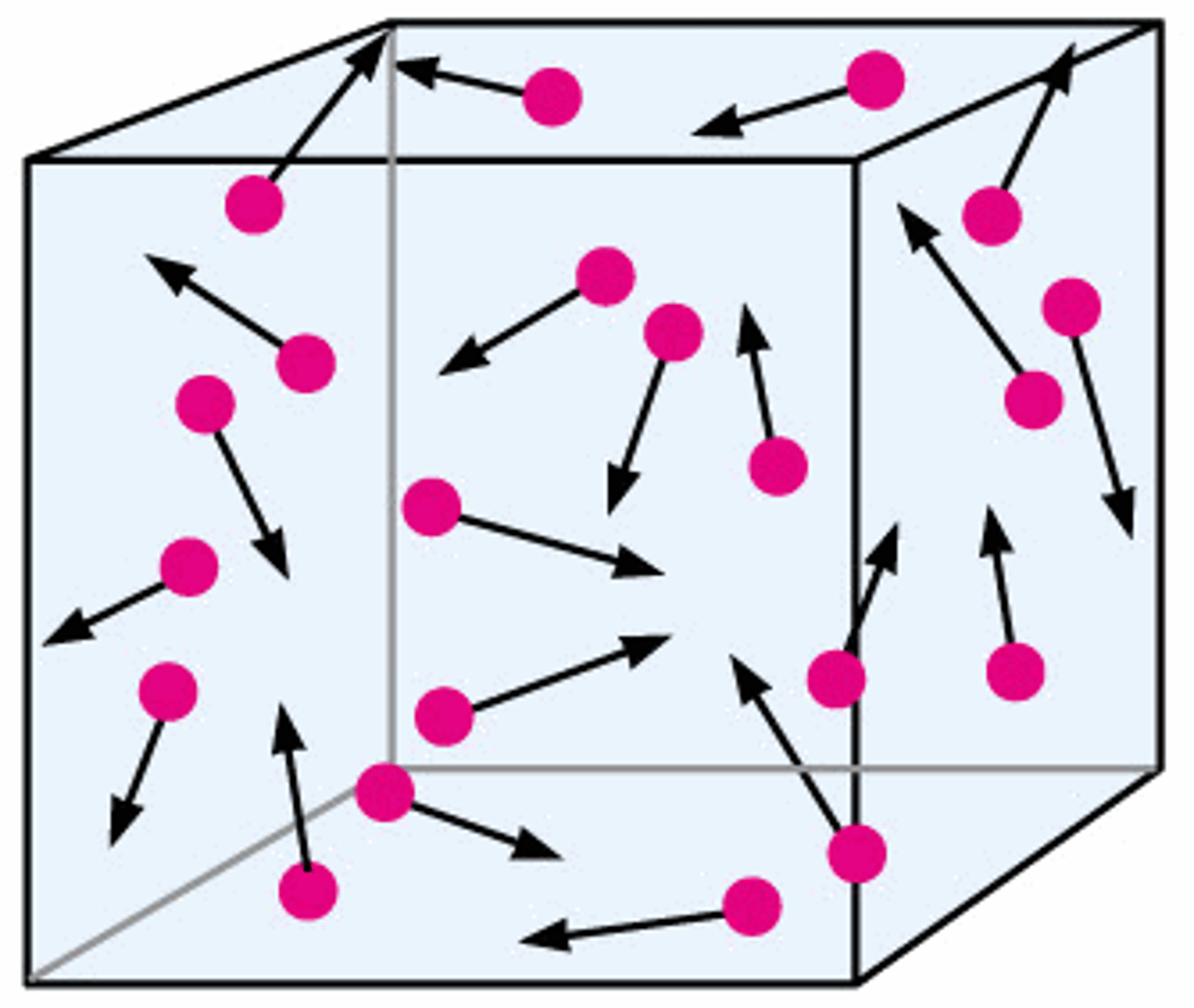
Brownian motion

= chaotic movement of colloidal particles, caused by collisions with particles of the solvent in which they are dispersed

proves existence of atoms because they are what collide with the larger particles, causing its path to change

Kinetic theory assumptions

- gases are in constant random motion and collisions are perfectly elastic

- collision duration is negligible compared to time between collisions

- motion follows Newton's laws

- no IM forces

- molecules move in straight lines

Ideal gas

a hypothetical gas that perfectly fits all the assumptions of the kinetic-molecular theory

only perfectly elastic collisions between the gas molecules => no intermolecular forces act between molecules => no potential energy => internal energy is only sum of KEs

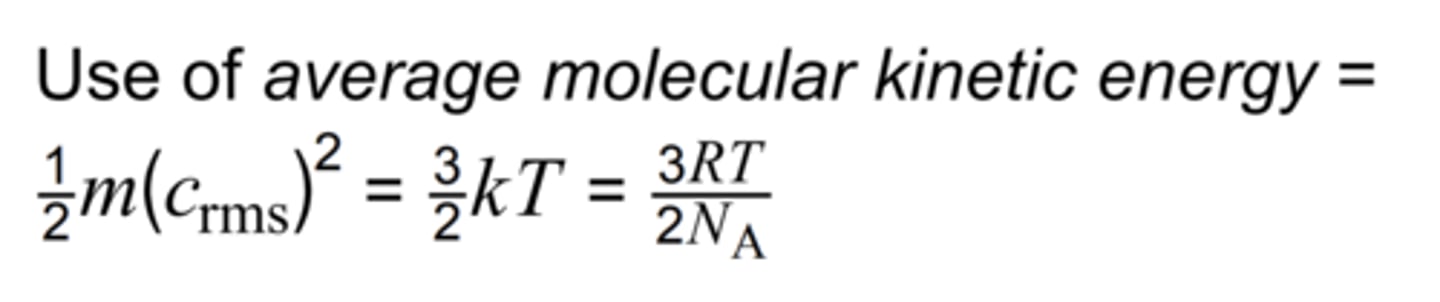
RMS speed

= speed of a molecule which has the average kinetic energy

more representative of maxwell's speed distribution, average velocity would be 0

find the mean of the squares

square root it

Derive kinetic theory model formula

consider one molecule in a box of length x, with speed u

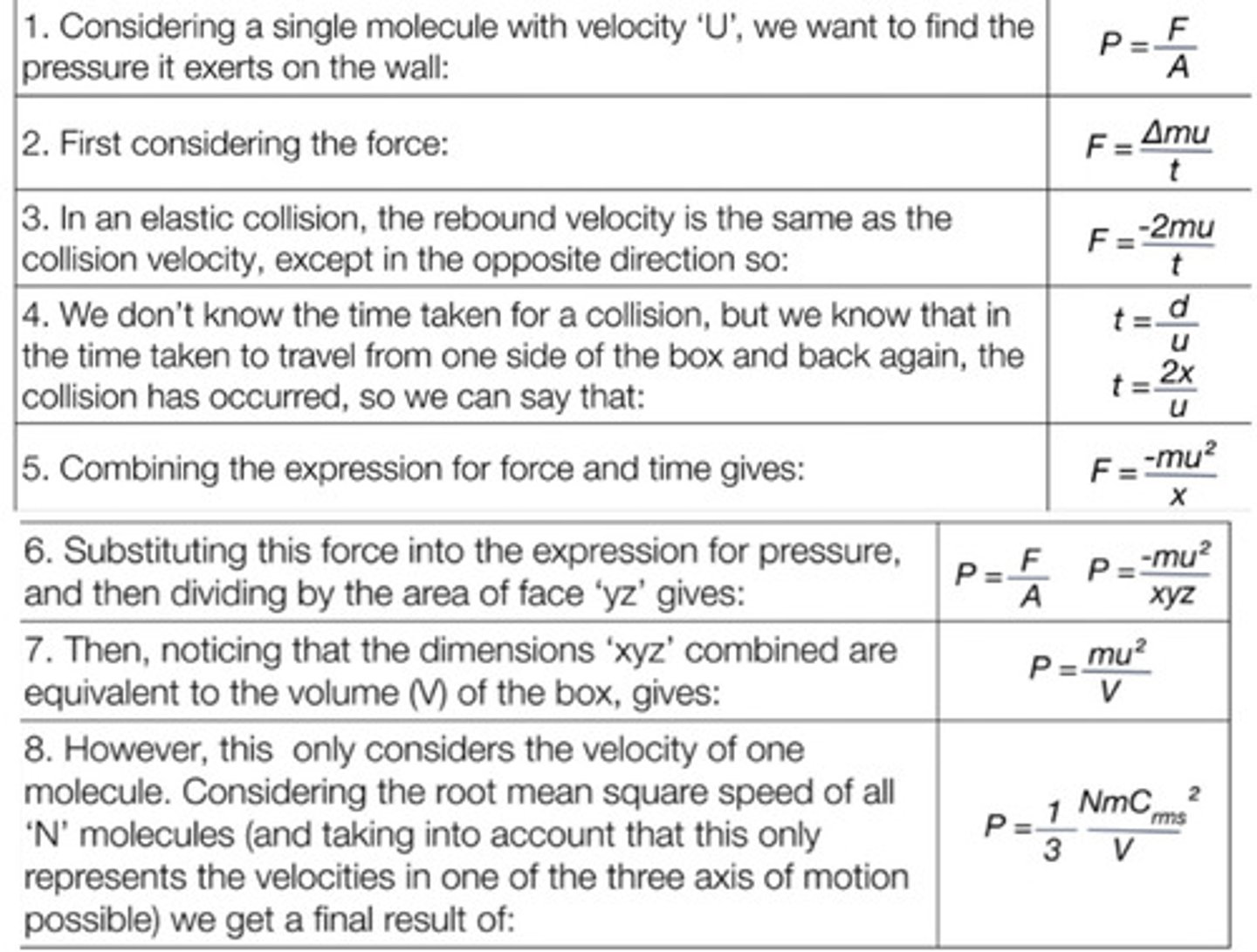
What is a force field?

How can they be represented?

How do they arise?

A region in which a body experiences a non-contact force.

Can be represented as a vector (e.g. a gravitational force field by lines directed towards the attracting body)

Arise from the interaction of mass, of static charge, and between moving charges.

(e.g. gravitational fields are formed during interaction of masses, electrical fields formed during interaction of charges)

What are the similarities and differences between gravitational and electrostation forces?

Similarities:

❆ Both force laws an inverse-square relation (e.g. F = GM₁M₂ / r²)

❆ Both use the “potential” concept.

❆ Both make use of field lines to indicate strength of field, and direction the field acts.

❆ Both have associated equipotential surfaces – surfaces that your potential remains constant over. Thus work done moving over an equipotential surface is 0J.

Differences:

❆ gravitational force is always attractive as masses always attract, but charges may attract or repel so electrostatic force can be attractive or repulsive

What is gravity?

a universal attractive force that acts between all matter due to their masses

What is Newton's Law of Gravitation?

the magnitude of the gravitational force between two masses is directly proportional to the product of the masses, and is inversely proportional to the square of the separation

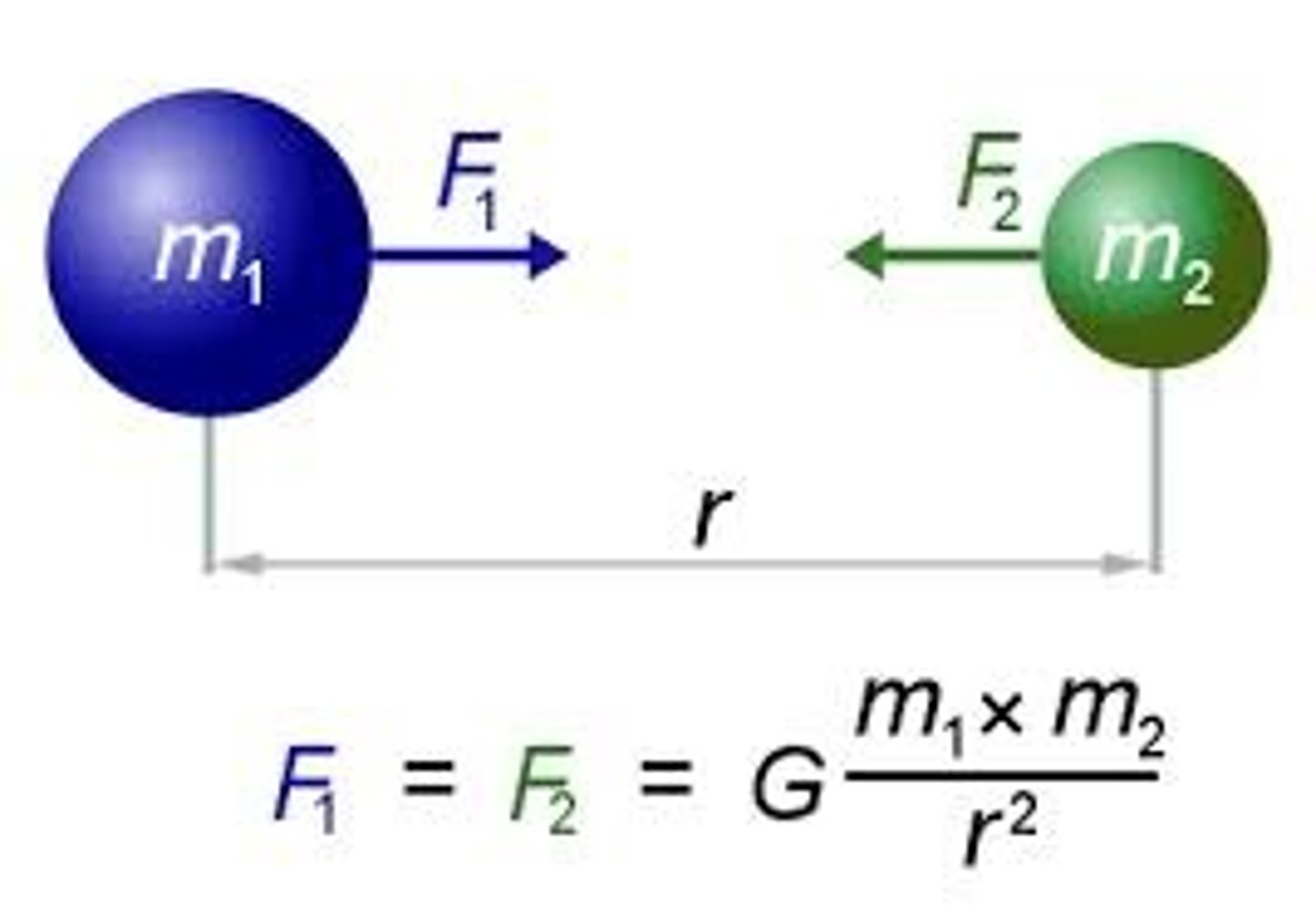
How is a uniform field represented with field lines?

How is a radial field represented with field lines?

Uniform

❆ straight, parallel, evenly spaced, with arrows (show the direction of the force acting on a small test mass, neglecting its gravitational force)

❆ surface of the Earth can be approximated as behaving as a uniform field

Radial

❆ field strength decreases as you move away from the mass - field lines become less dense

What is g?

How is g determined in a uniform field?

How is g determined in a radial field?

force per unit mass, unit for gravitational field strength

in a uniform field, g = F/m

in a radial field, g = GM / r²

[this is because F = mg and F = GMm / r²]

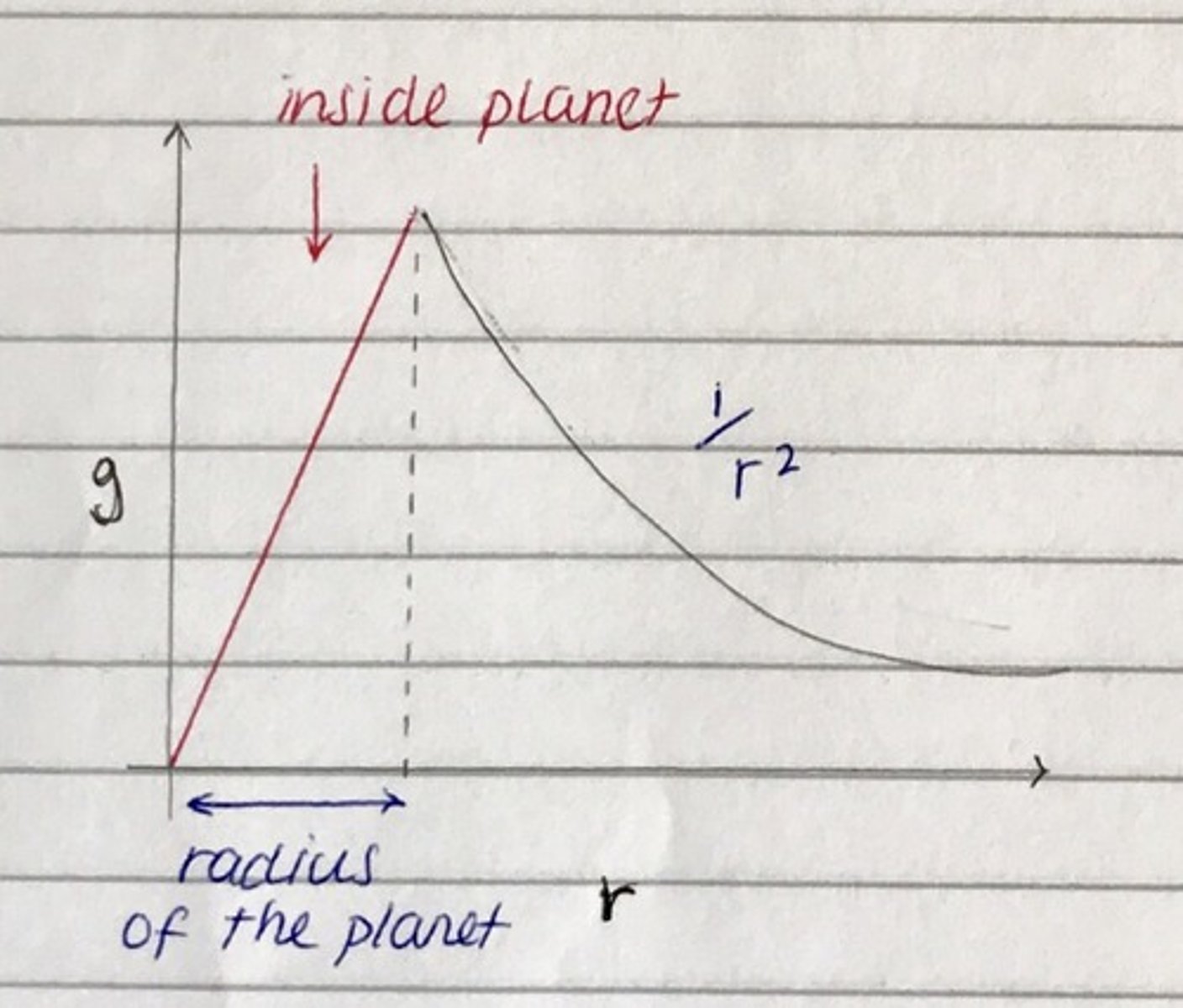
Show that g ∝ r inside a planet when considering the gravitational field as uniform.

g = GM / r²

V = 4/3 π r³

M = ρV

=> substitute all this together and end up with:

g = 4/3 π G ρ r

=> therefore, g = kr, therefore g ∝ r

What is the definition of gravitational potential?

Gravitational potential is the work done per unit mass against gravitiational force to move an object from infinity to a given point.

e.g. the Earth’s surface has a gravitational potential of -63MJ/kg, so to move a 1kg mass from the surface of the Earth to infinity, we must do 63MJ of work.

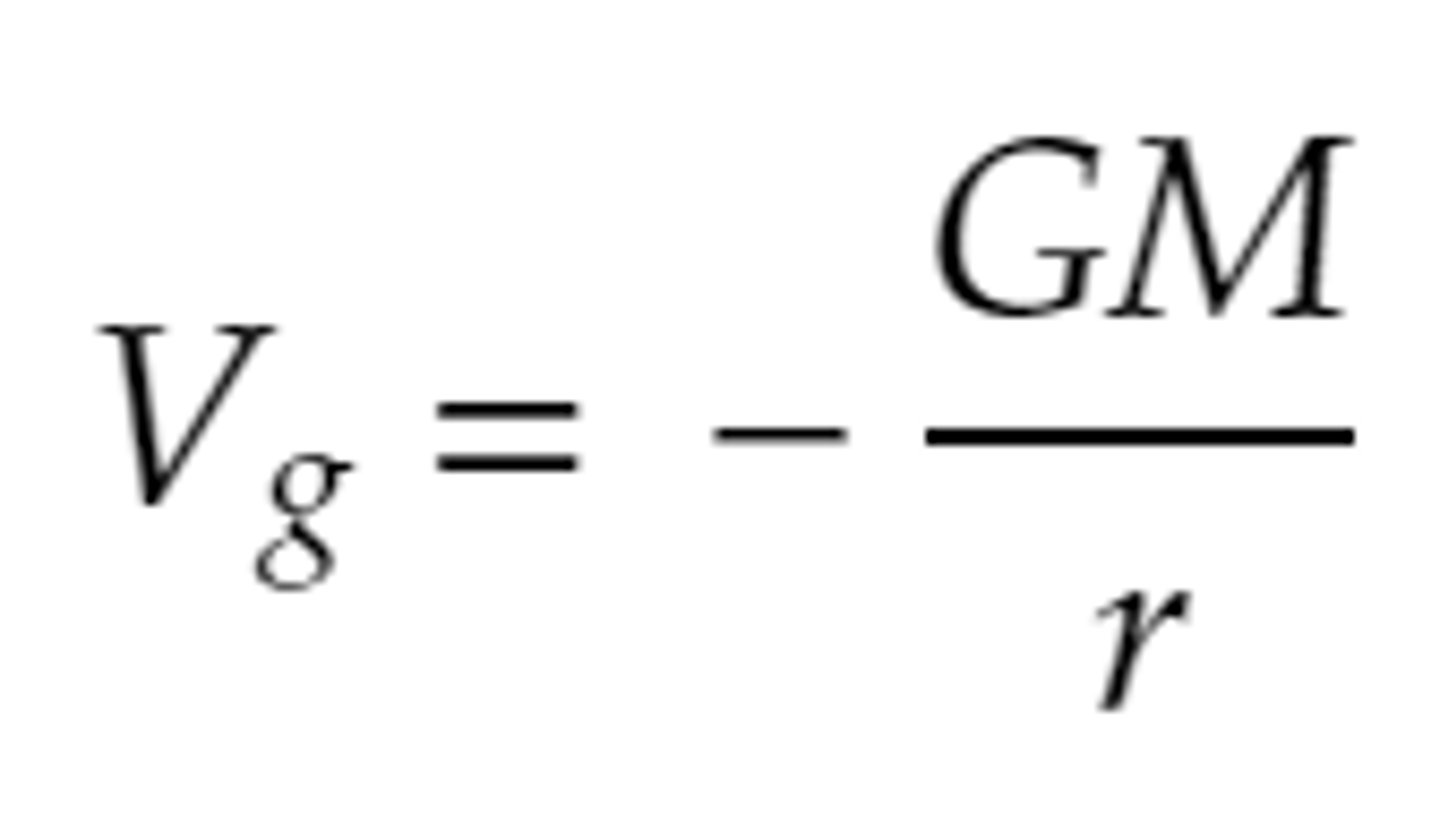
Why is gravitational potential negative?

gravitational potential is zero at an infinite distance away, as this is a constant.

zero is the maximum possible value of V

so all points below infinity have V < 0 => negative

What is gravitational potential difference?

the difference in potential between two points in a gravitational field

ΔV = ΔW / m => change in work done per unit mass

V at Earth's surface ≈ -63MJ/kg

V at 1000km Earth's surface ≈ -54MJ/kg

ΔV = -54 - (-63) = 9MJ/kg

What equation gives the work done in moving a mass between two points on a gravitational field?

ΔW = ΔV · m

What is an equipotential surface?

surfaces which are created through joining points of equal potential together, so the potential is constant everywhere on the surface

this means ΔV = 0 when moving across the surface, so no work is done when moving across the surface

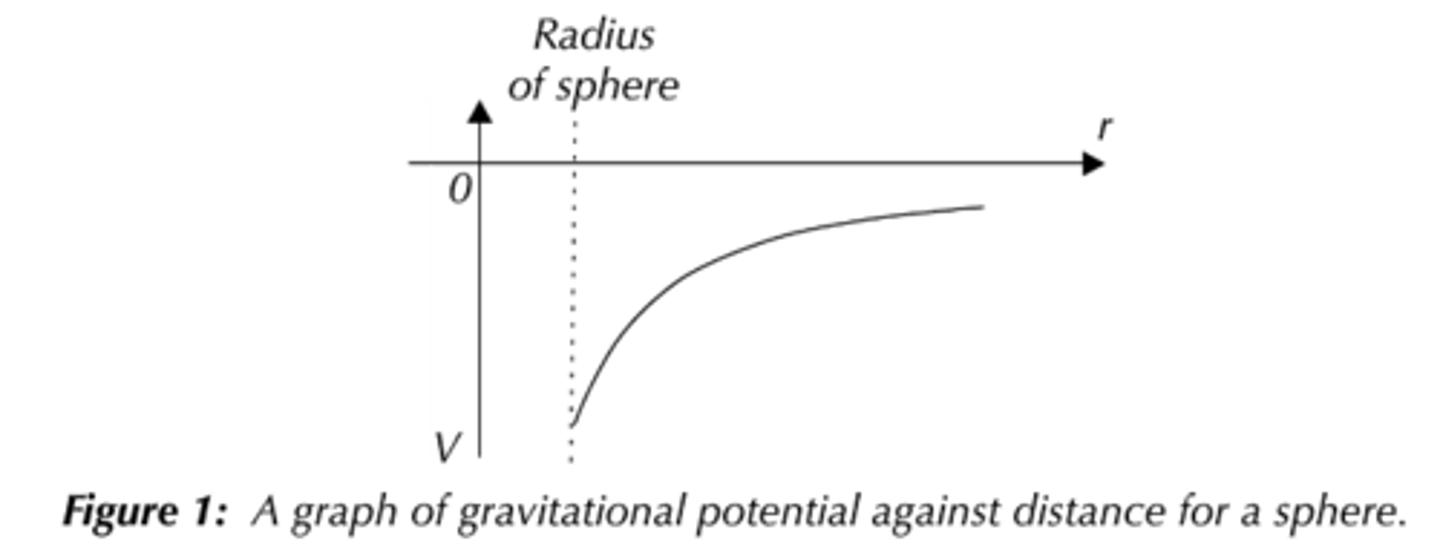
What formula is used to calculate V in a radial field?

Graph: V against r

what does it look like?

what does the gradient represent?

gradient represents field strength

this might have a negative e.g. g = -ΔV/dr, which signifies the direction of the field as pointing towards the big object

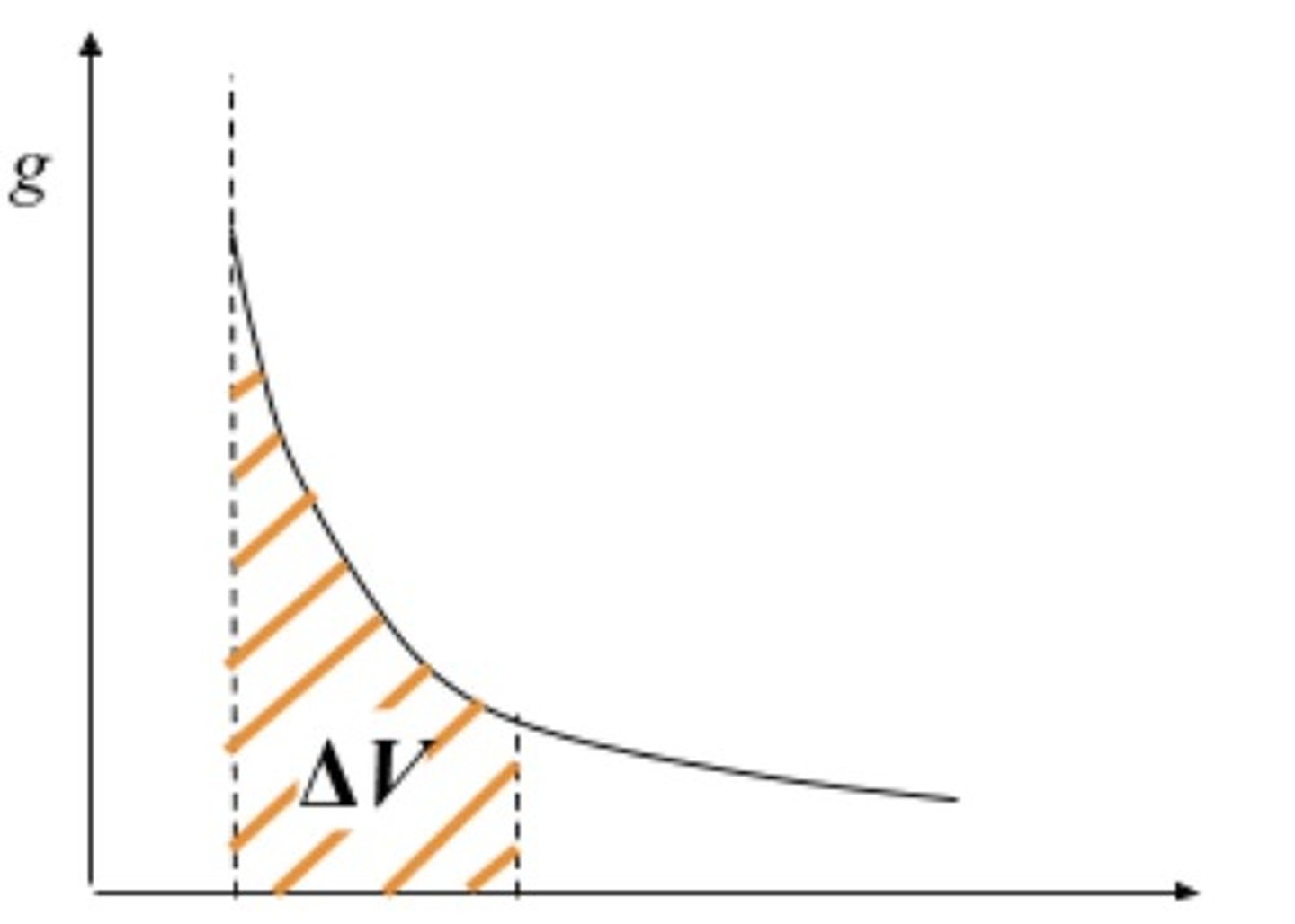
How do you calculate ∆V from graph of g against r?

What types of energy does a satellite have?

How would you calculate the total energy of a satellite?

kinetic energy (result of its velocity and mass)

gravitational potential energy (result of its position in the gravitational field and its mass)

total energy = KE + GPE

or, as a simple formula, E = GMm / 2r

What would happen if the satellite was moved closer to the Earth?

❆ it would lose gravitational potential energy

❆ energy must be converted to kinetic energy

❆ so velocity increases - to back this up, v = root (GM / r)

❆ so orbital time decreases

What is a synchronous orbit?

What period would a geostationary satellite have?

an orbit in which an orbiting body (usually a satellite) has a period equal to the average rotational period of the body being orbited (usually a planet), and in the same direction of rotation as that body

geosynchronous => satellite has period = rotational period of the Earth = 24hrs

can have any inclination and eccentricity and may not be a circular orbit

What is escape velocity?

What is the equation to work out the escape velocity, and how to derive it?

Black holes

the lowest velocity that a body must have in order to escape the gravitational attraction of a particular planet or other object

in black holes, even light cannot escape, so we can set the escape velocity to c (this would be the minimum escape velocity for a black hole)

[side note: Schwarz-Child radius = radius a body has to be to become a black hole]

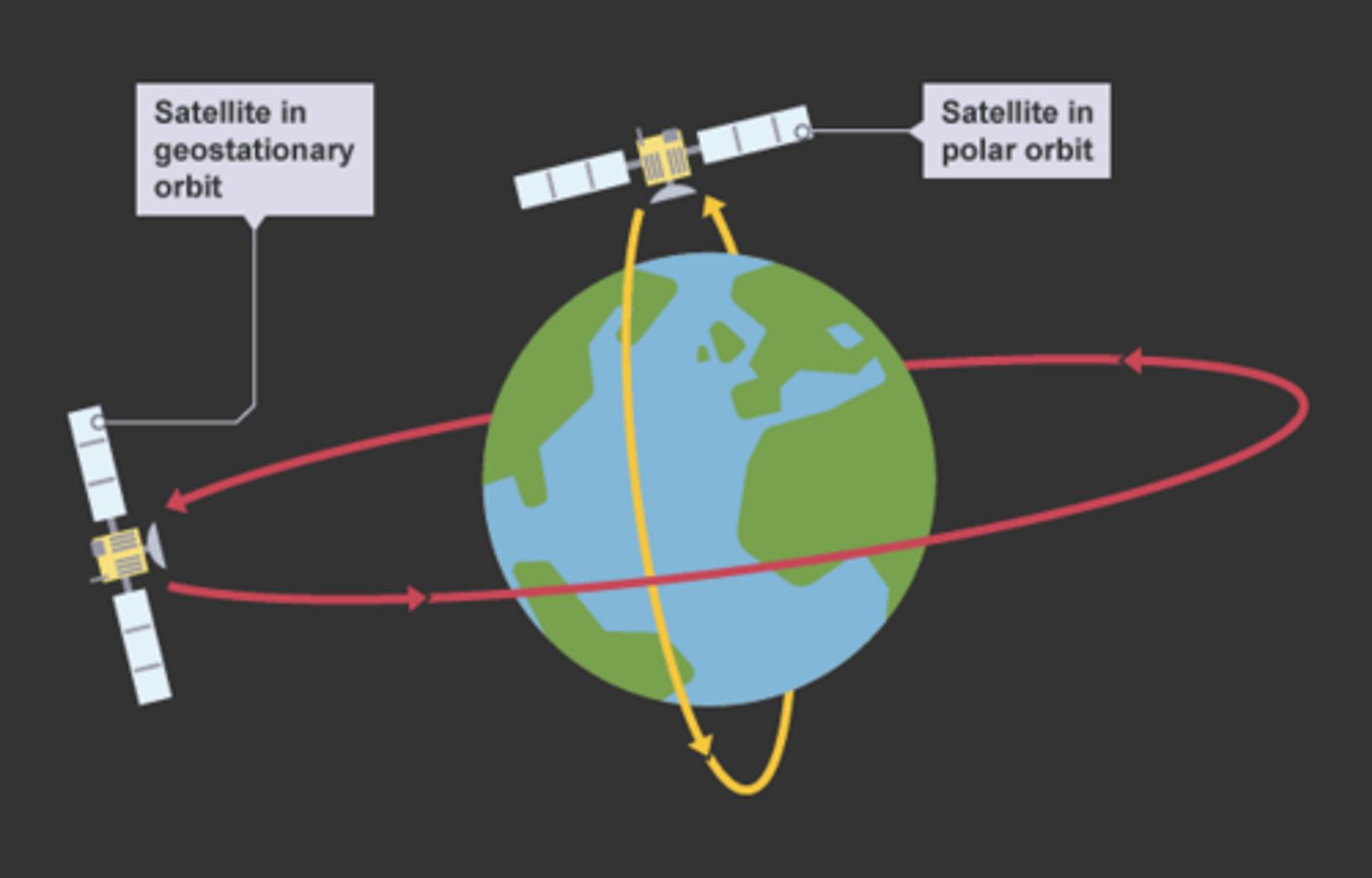
Geosychronous vs low / polar orbit satellites

Geosynchronous

❆ orbital period matches the Earth’s rotational period = 24hrs

❆ maintains the same position relative to the Earth.

❆ travels west to east above the Equator (same direction as the Earth’s rotation).

❆ stays above same part of Earth throughout rotation

❆ orbital height > polar orbit

❆ speed < polar orbit

❆ scans fixed area of the Earth’s surface

❆ applications: telecommunications, cable and satellite TV, radio

❆ requires higher signal strength

Polar orbit

❆ orbital period = few hours.

❆ orbital height < geostationary orbit

❆ orbital speed > geostationary orbit

❆ applications: surveillance i.e. mapping, weather observations or environmental monitoring.

❆ requires lower signal strength

❆ Earth moves relative to the orbit of the satellite

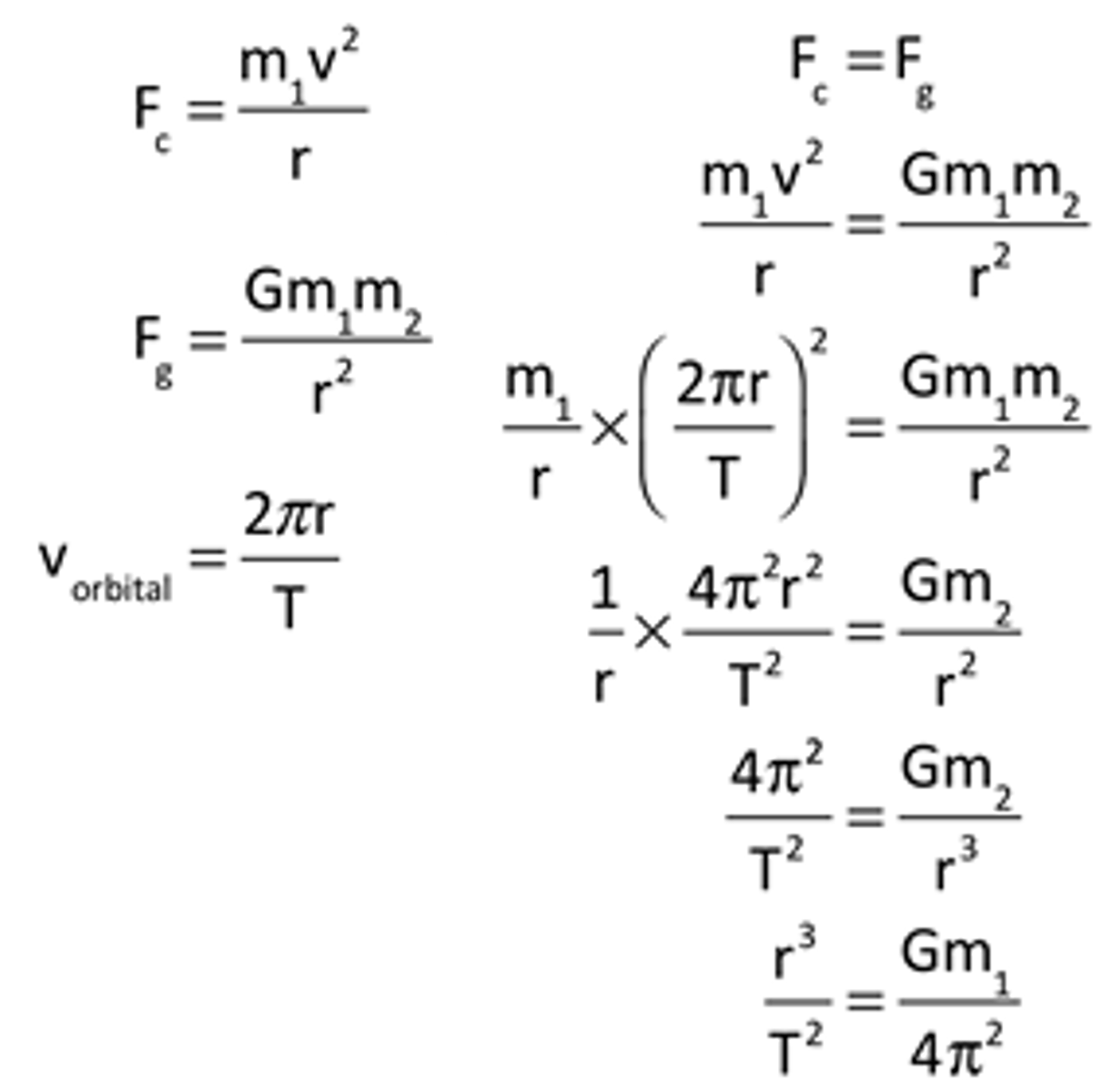
How is the orbital period and speed of a satellite related its orbital radius?

smaller radius => faster speed (v = root (GM / r))

smaller radius => smaller time period (T² ∝ r³)

Show that r³ / T² = Gm / 4π², where m is the thing that is not orbiting.

Also, derive T² ∝ r³

Describe two properties of a radial field

- field lines perpendicular to the surface and equally spaced at the surface (then spread out)

- equipotential surfaces are spherical

- field strength decreases with distance

- force acting decreases with distance

What is Coulomb's law?

calculates force between two electrically charged particles

the magnitude of the electrostatic force between two charges is directly proportional to the product of the charges, and is inversely proportional to the square of the separation

k is constant => 1/(4πℇ₀), and roughly equal to 8.99x10⁹

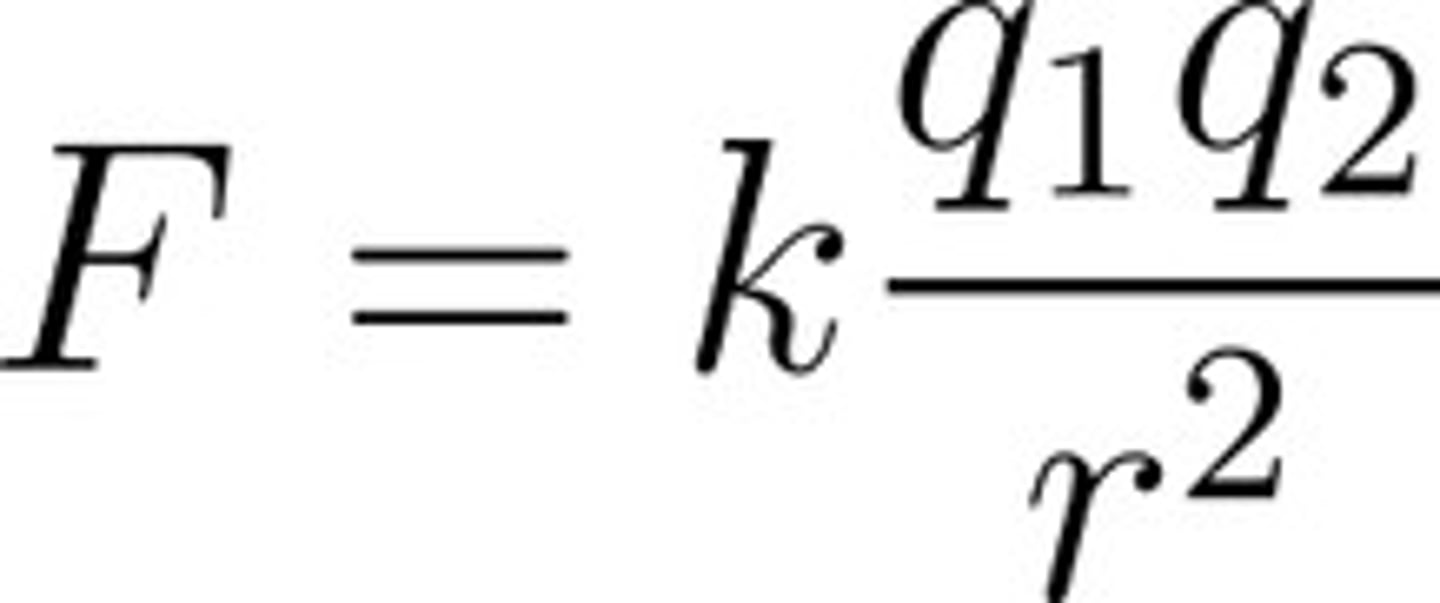
A negative force from Coulomb's law signifies a ________ force

A positive force from Coulomb's law signifies a ________ force

A negative force from Coulomb's law signifies an attractive force => because one charge must be -ve and one must be +ve

A positive force from Coulomb's law signifies a repulsive force

What is ℇ₀?

permittivity of free space => shows capacity of electrical fields to go through a vacuum

note: air can be treated as a vacuum

Compare the magnitude of gravitational and electrostatic forces between subatomic particles.

magnitude of electrostatic forces is magnitudes greater than the magnitude of gravitational force

this is because the masses of subatomic particles are incredibly small whereas their charges are larger.

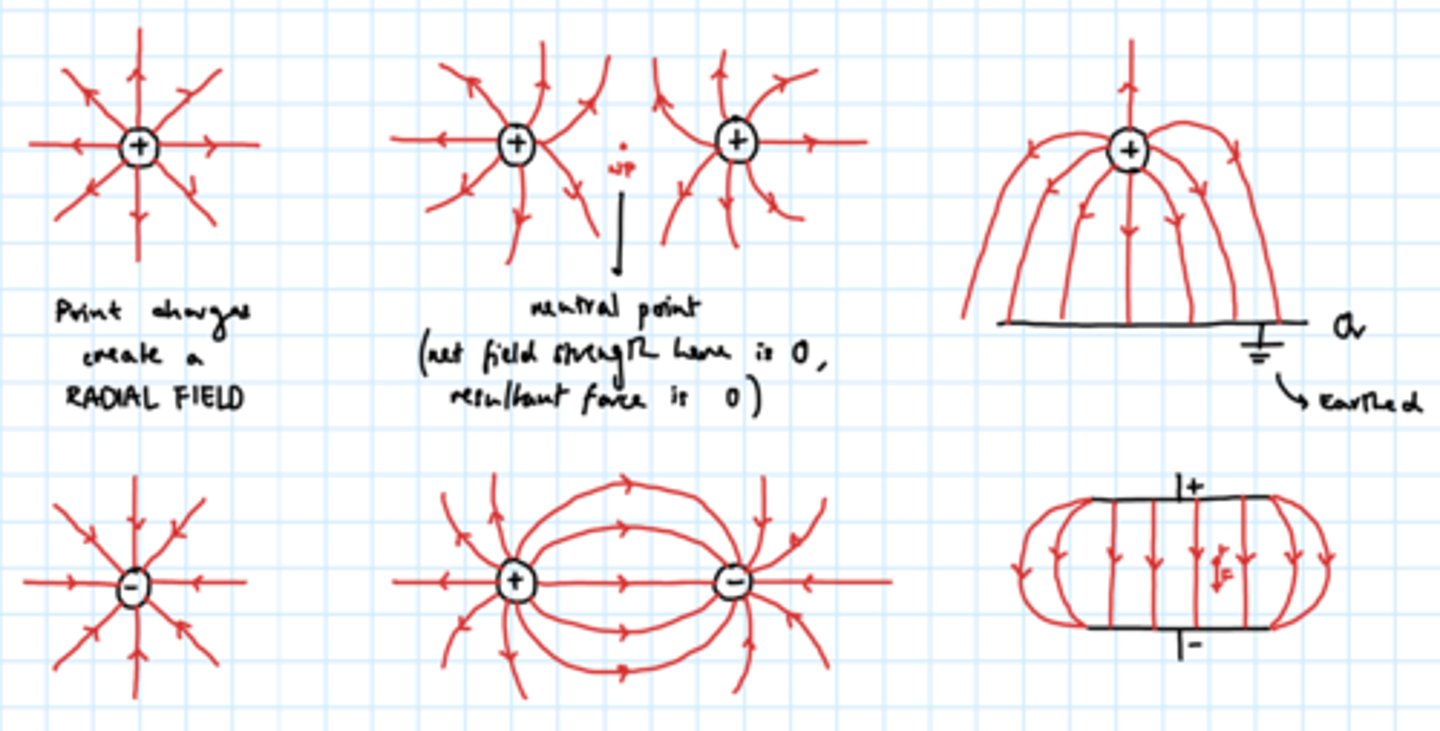
Representing electric fields with field lines:

✢ uniform

✢ radial

✢ between two positive charges

✢ between a positive and negative charge

in all cases: arrows drawn positive to negative

uniform (e.g. parallel plates): straight, parallel, evenly spaced

radial (e.g. point charges): like rays of the sun => less dense further from pt charge => force weaker

What is the definition of electric field strength?

force per unit positive charge

in a uniform field: F / Q⁺ or V / d

in a radial field: kQ / r²

where k = 1/(4πℇ₀), and roughly equal to 8.99x10⁹

Show that, in a uniform electric field, E = V / d, where d = the distance between the two plates.

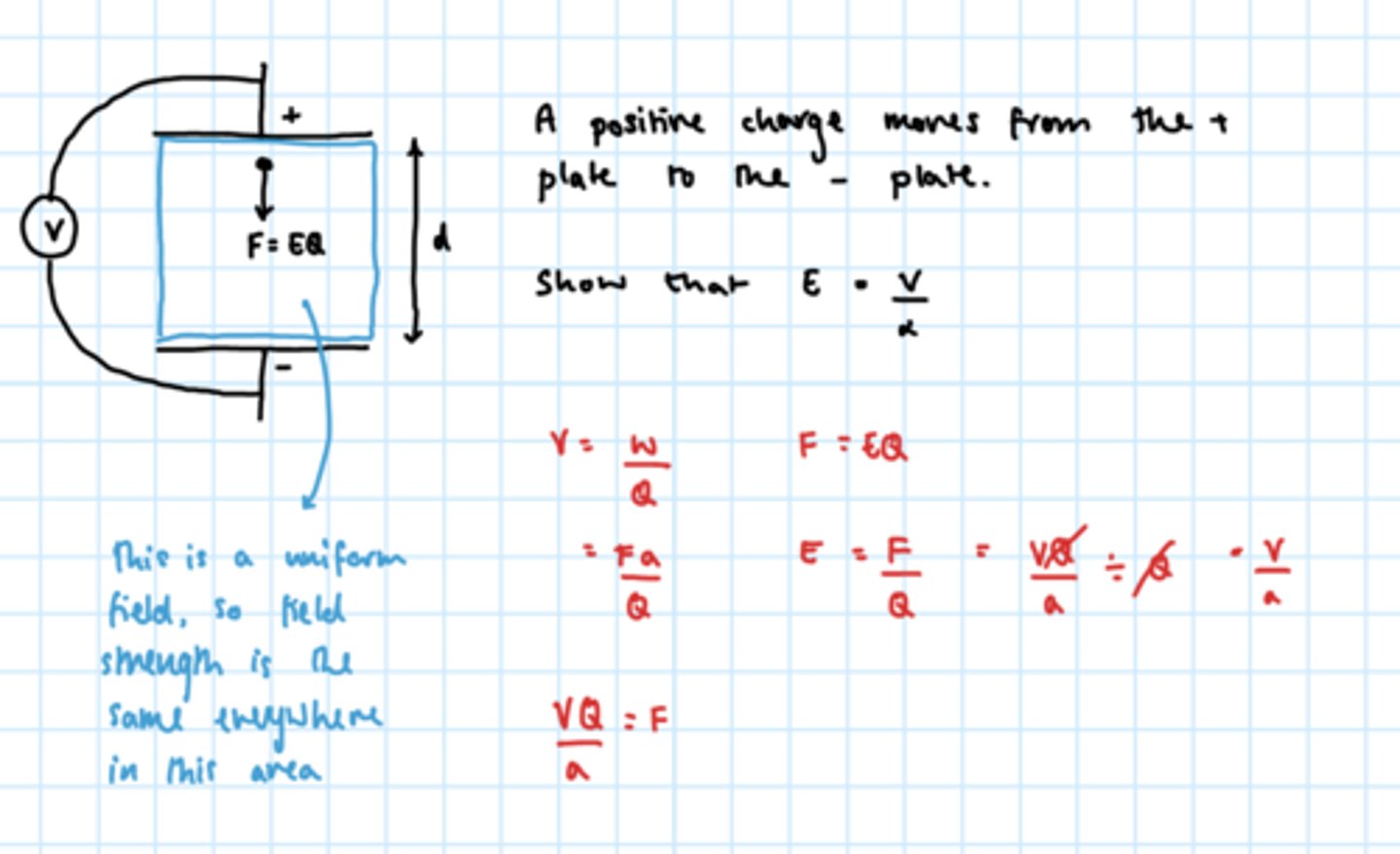
Field strength is the same everywhere in a uniform field.

True or false?

True

What is an eV, and what is 1eV in J?

= work done in moving an electron through a potential difference on 1V

W = VQ = 1 × 1.6ⅹ10⁻¹⁹J

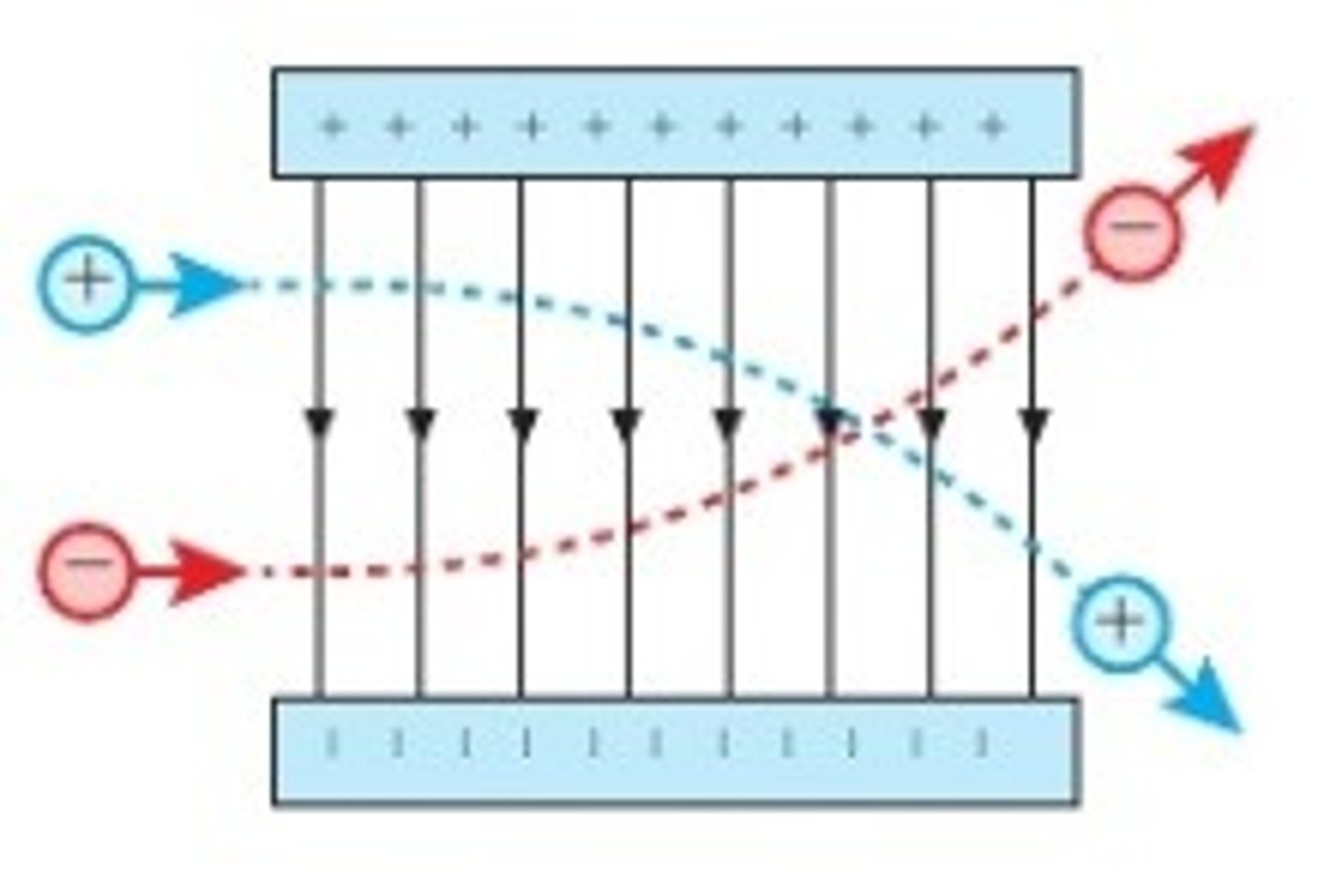
A moving charged particle enters a uniform electric field at right angles to the field.

Calculate the vertical displacement when it reaches the end of the plate.

What are the things to calculate, and how?

PARABOLIC MOTION (constant x speed, accelerating due to force in y)

E => E = V / d

F => F = EQ

acc. => F = ma

vel. => KE = ½mv²

time => v = d / t

disp. => s = ut + ½at² (remember vertical u = 0)

What is the definition of, and formula for, electric potential?

work done per unit positive charge in moving a test positive charge from infinity to a given point

has a value of 0 at an infinite distance away, although can be +ve (if charge +ve) or -ve (if charge -ve)

V = kQ / r

where Q = charge of 'planet' thinking in gravitational terms

What is electric potential difference?

the difference in potential between two points in an electric field

Formula to calculate work done in moving a charge Q.

ΔW = QΔV

A GENERAL NOTE:

at a point between two charged particles:

when working out the total electric field strength => consider direction

when working out the total electric potential => scalar addition

What is an equipotential surface?

How are equipotentials drawn from field lines?

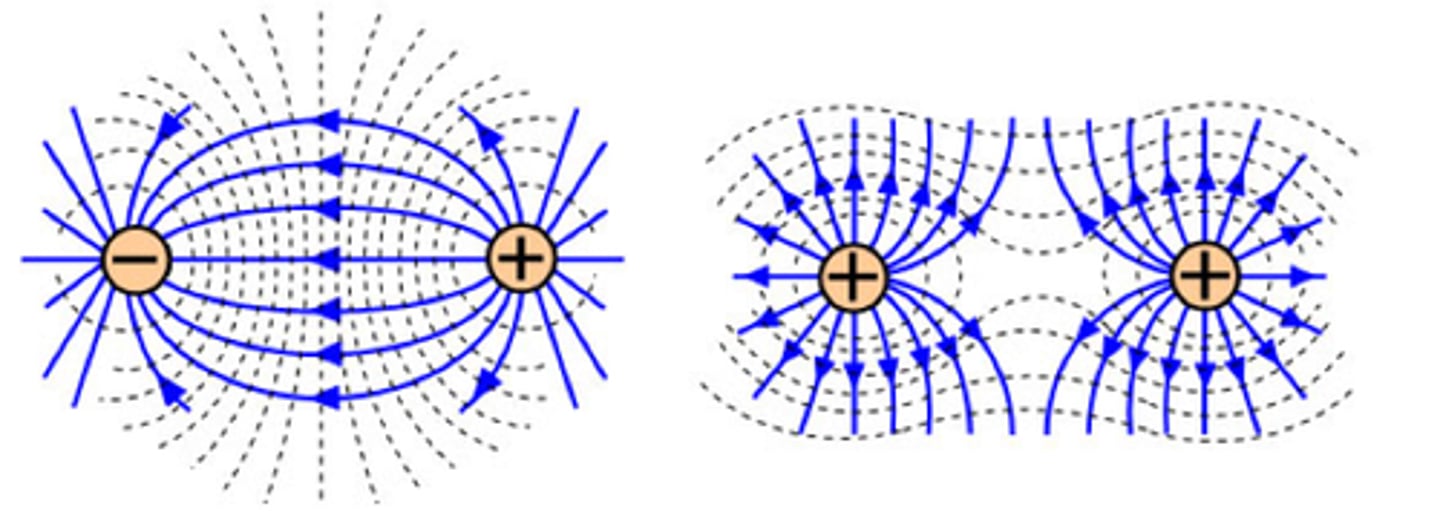
surfaces which are created through joining points of equal potential together, so the potential is constant everywhere on the surface

this means ΔV = 0 when moving across the surface, so no work is done by a charge when moving across the surface

equipotentials are drawn perpendicular to field lines

What would the electric field and equipotential lines look like for:

✢ between two positive charges?

✢ between a positive and negative charge?

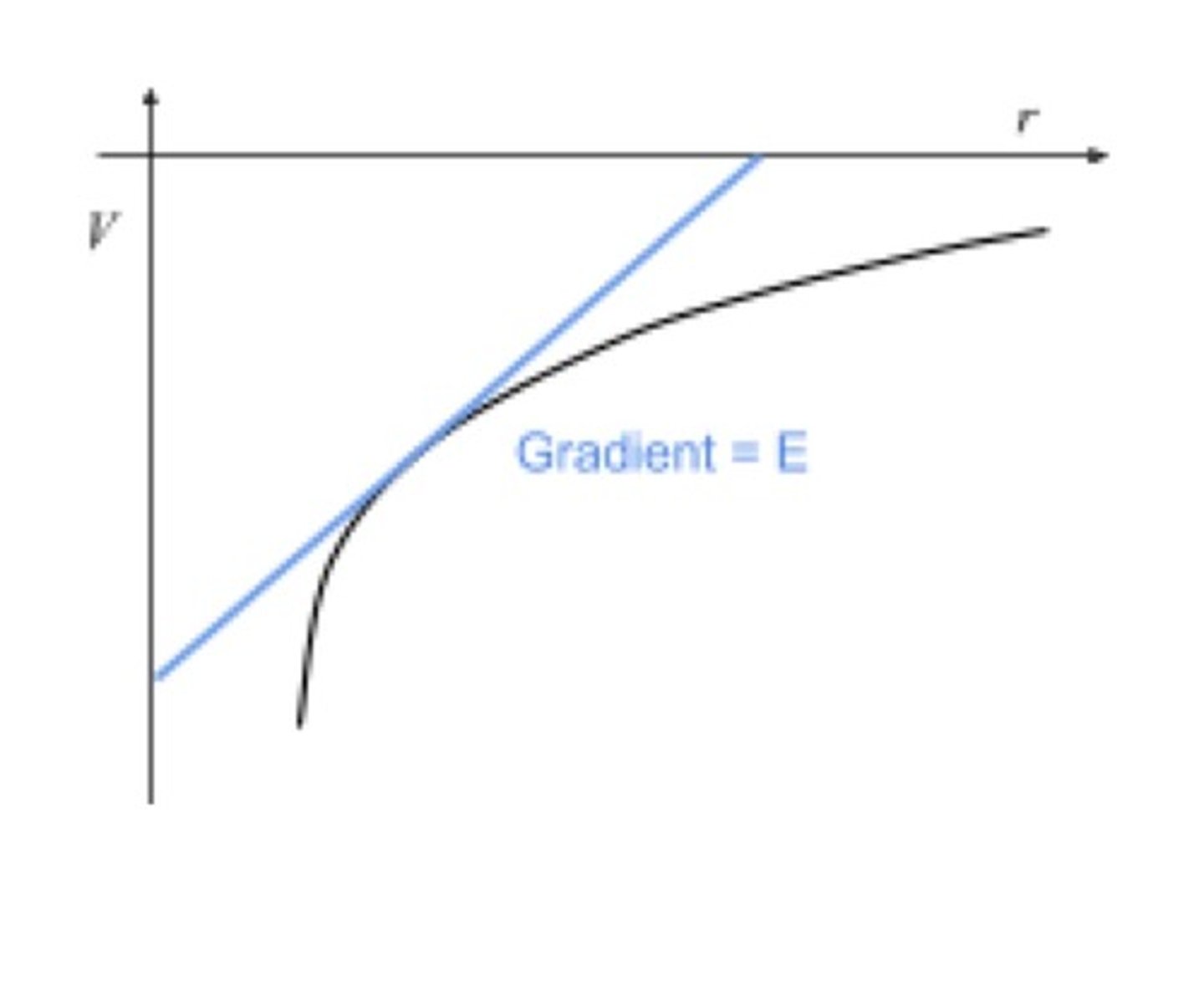
Graph: V against r:

✢ what does it look like?

✢ what does the gradient represent?

gradient represents field strength

this might have a negative e.g. E = -ΔV/dr, which signifies the direction of the field as pointing towards the big object

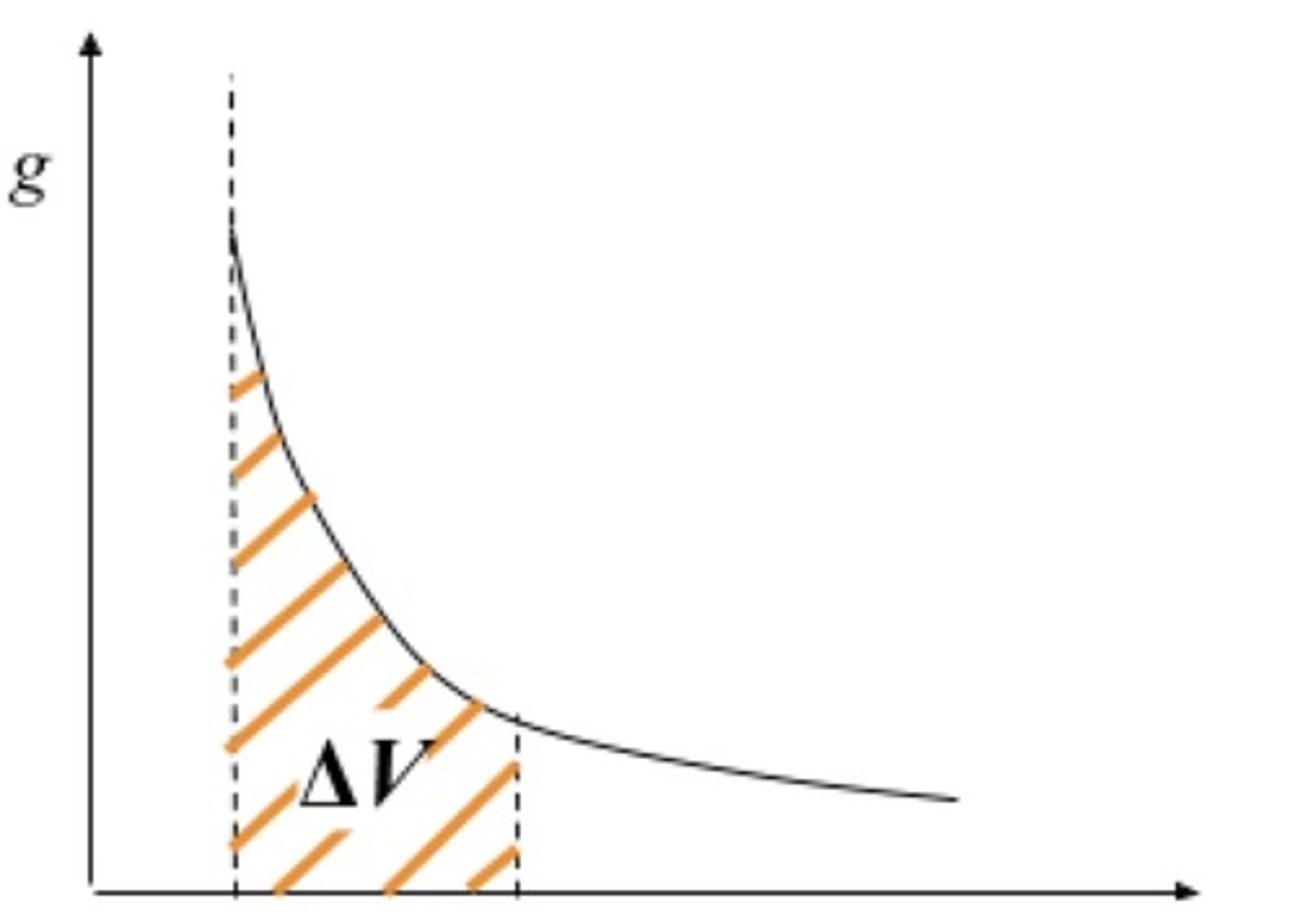
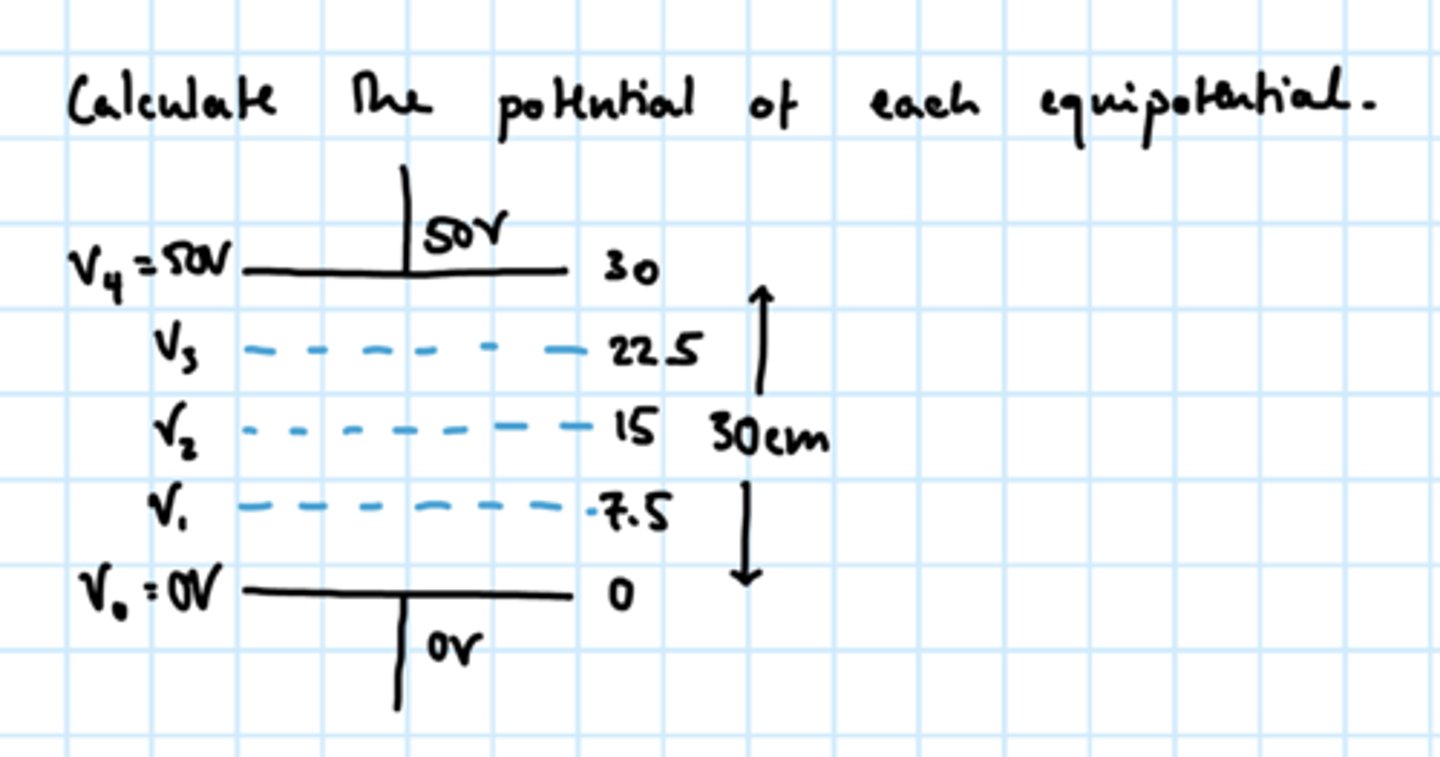
How do you calculate ∆V from graph of g against r?

V₁ = 12.5V

V₂ = 25V

V₃ = 37.4V

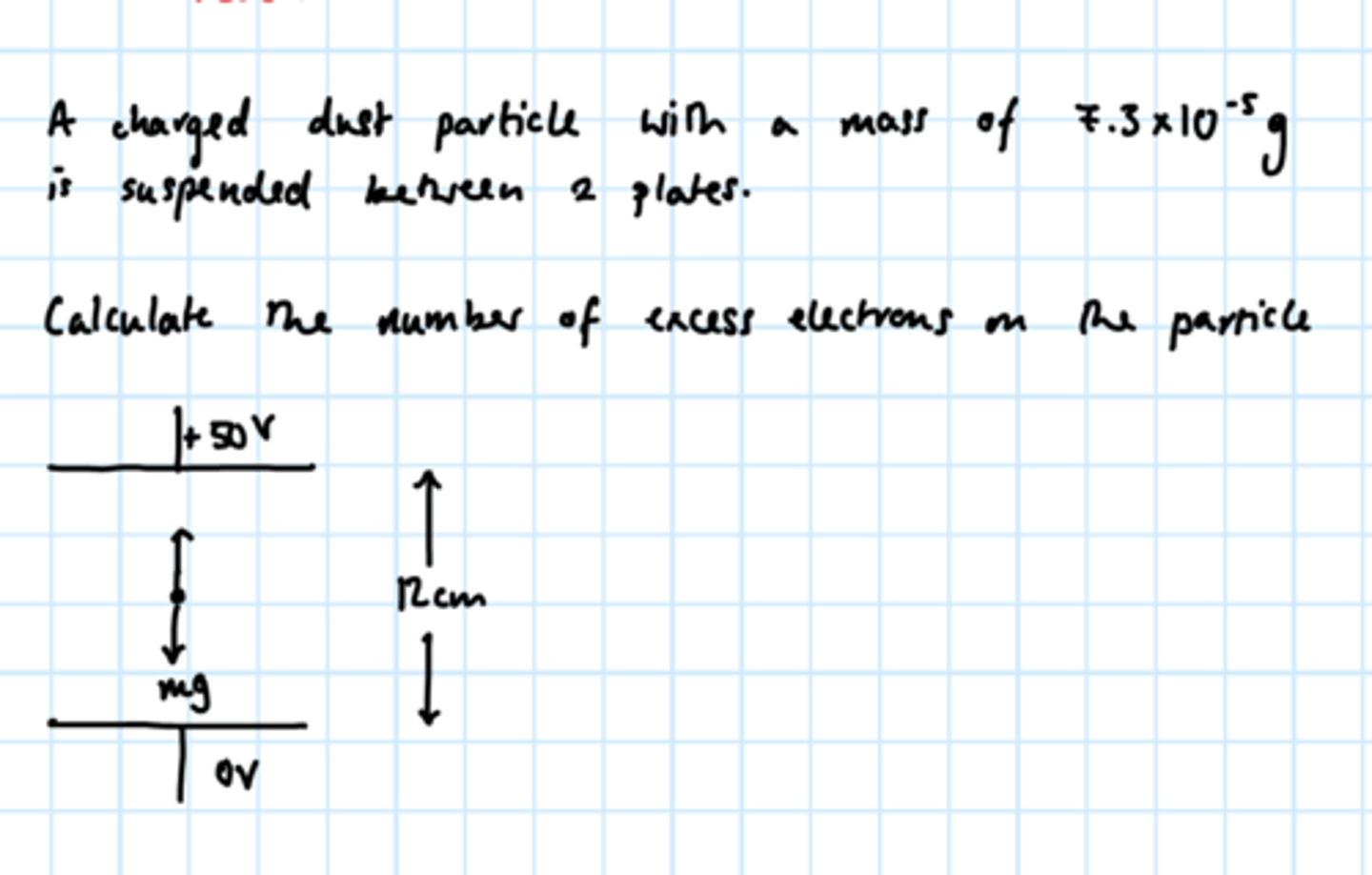
1.07 x 10¹⁰

should have been mass x 10-8

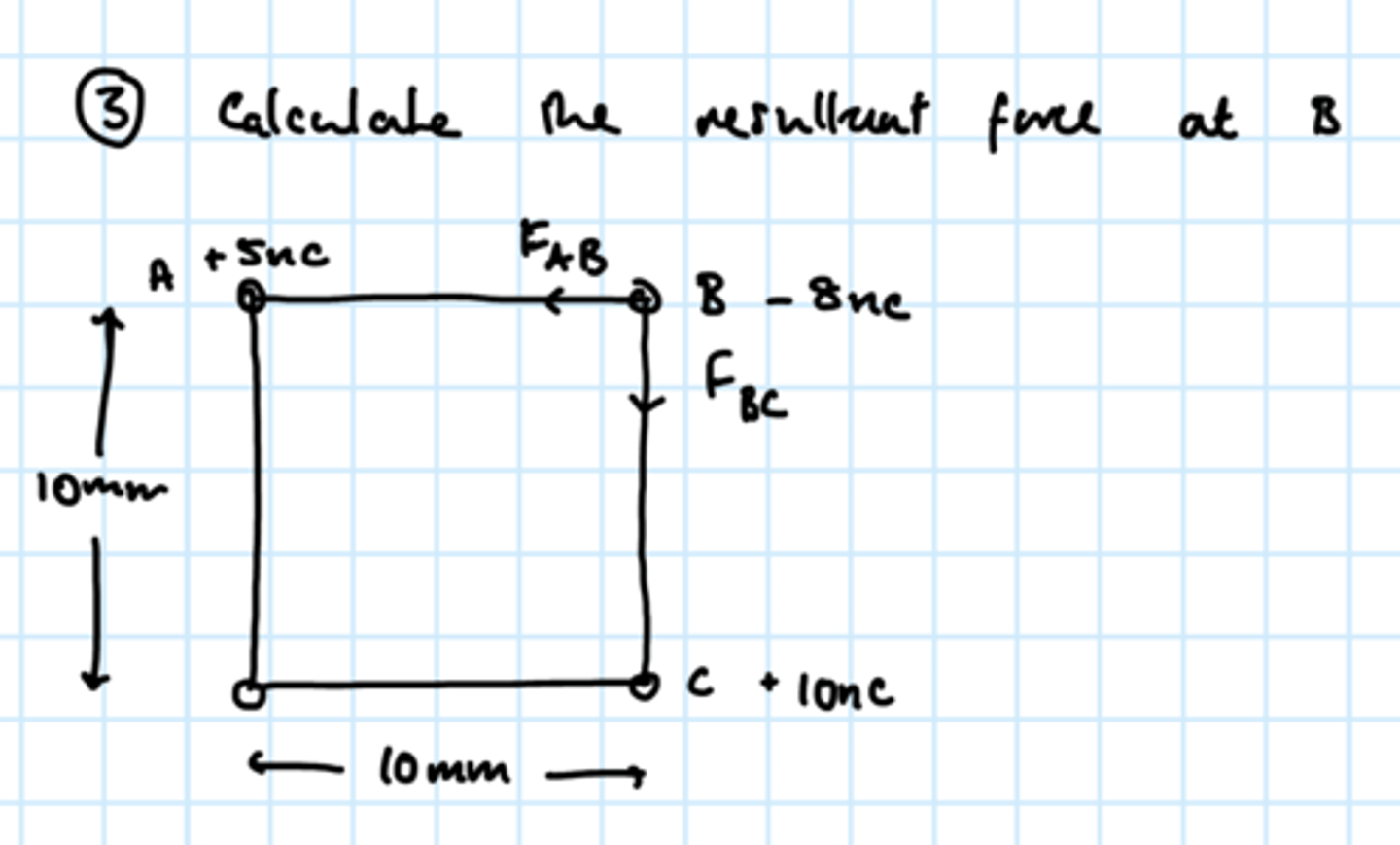
8 x 10⁻³N

60° below horizontal

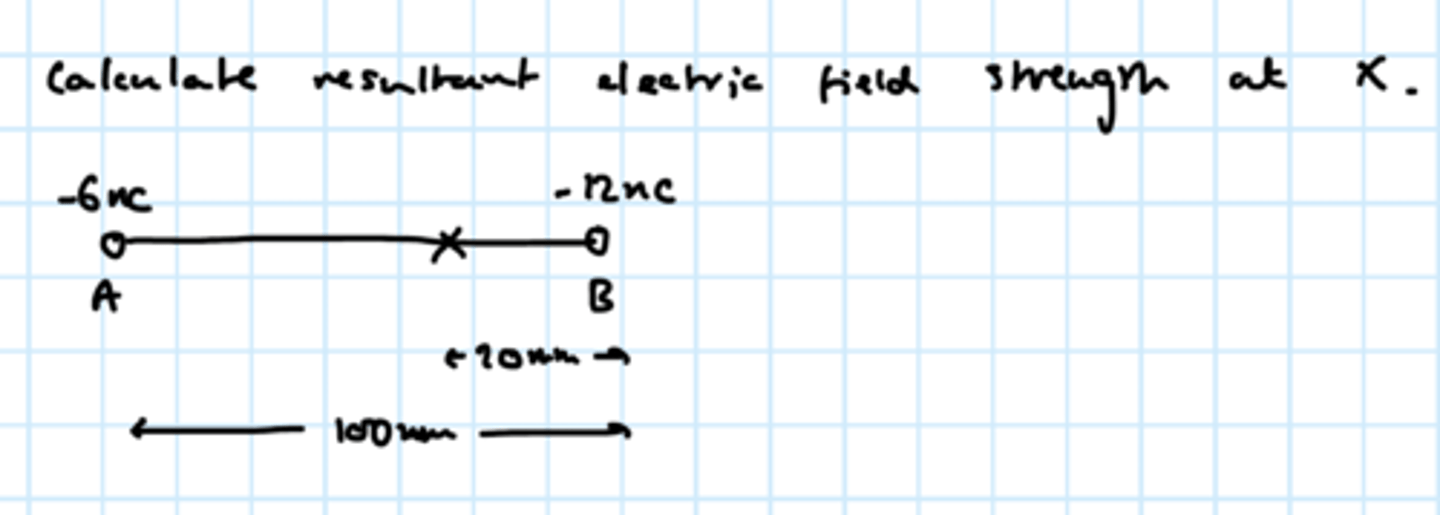
1.6 x 10⁻⁶ C

angle at top = 35 degrees

2.6 x 10⁵ NC⁻¹

0.053J

Definition of capacitance

Unit of capacitance

capacitance = charge per unit volt

C = Q / V

measured in Farads (1F is very large, check working if you get this)

can think of it as the information per unit effort => some students have a higher 'capacitance' i.e. they put in less effort for the same information as others

What is a Farad defined as?

1 coulomb per unit volt

unit of capacitance

Capacitor - what is it?

How does charging a capacitor work? (there's a picture of a circuit on the other side)

a device used to store charge in a circuit

two conducting parallel plates with an insulator between them

1. current flows around circuit

2. electrons build up on bottom plate - they can't get across the dielectric / gap between plates => capacitor becomes charged

3. a uniform electric field forms

4. electrons on bottom plate displace electrons on top plate => top plate becomes positively charged

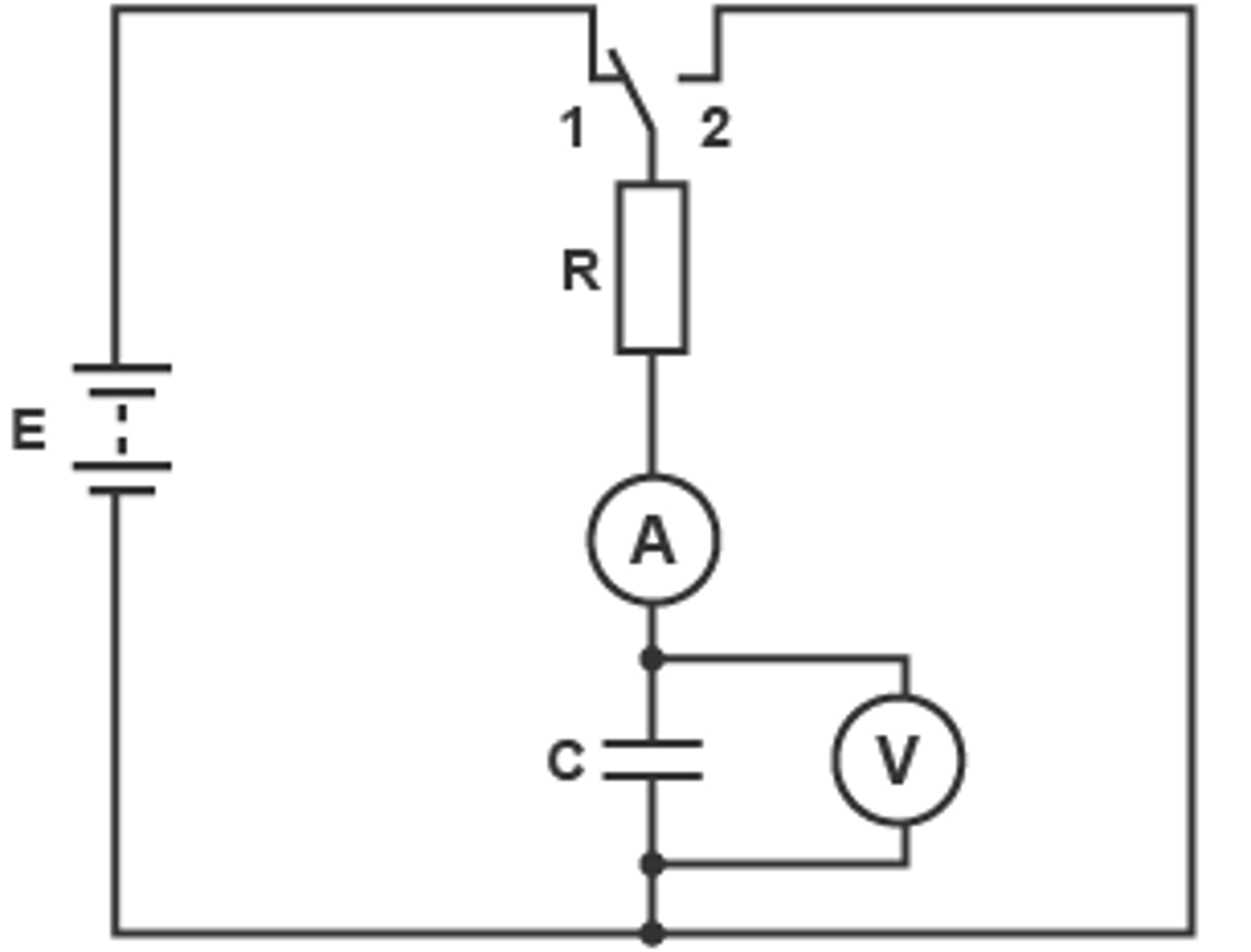
How to tell which side of the capacitor gets negatively charged?

electrons come out of negative terminal (small side)

then they get stuck on the first plate => this plate gets negatively charged

A capacitor of 100mF is initially uncharged, is placed in a circuit in series with a 50kΩ resistor and is then attached to a 9.0V power supply.

1. Calculate the initial current flowing through the circuit when it is completed.

2. State the initial p.d. across the resistor when the circuit is first completed.

3. State the initial p.d. across the capacitor when the circuit is first completed

4. Calculate the maximum charge the capacitor can store in this circuit.

Initially, there is no p.d. across the capacitor => p.d. across resistor is 9.0V

1. V = IR ∴ I = 9.0 / 50,000 = 1.8 x 10⁻⁴

2. 9.0V

3. 0.0V

4. C = Q / V ∴ Q = 100 x 10⁻³ x 9.0 = 0.9C

What effect does resistance in the circuit have on the rate of charging of the resistor?

no resistance: I₀ = ∞

so rate of flow (current) is ∞

so charging happens instantaneously

very large resistance: I₀ = lower

so rate of flow (current) is lower

so takes longer to charge

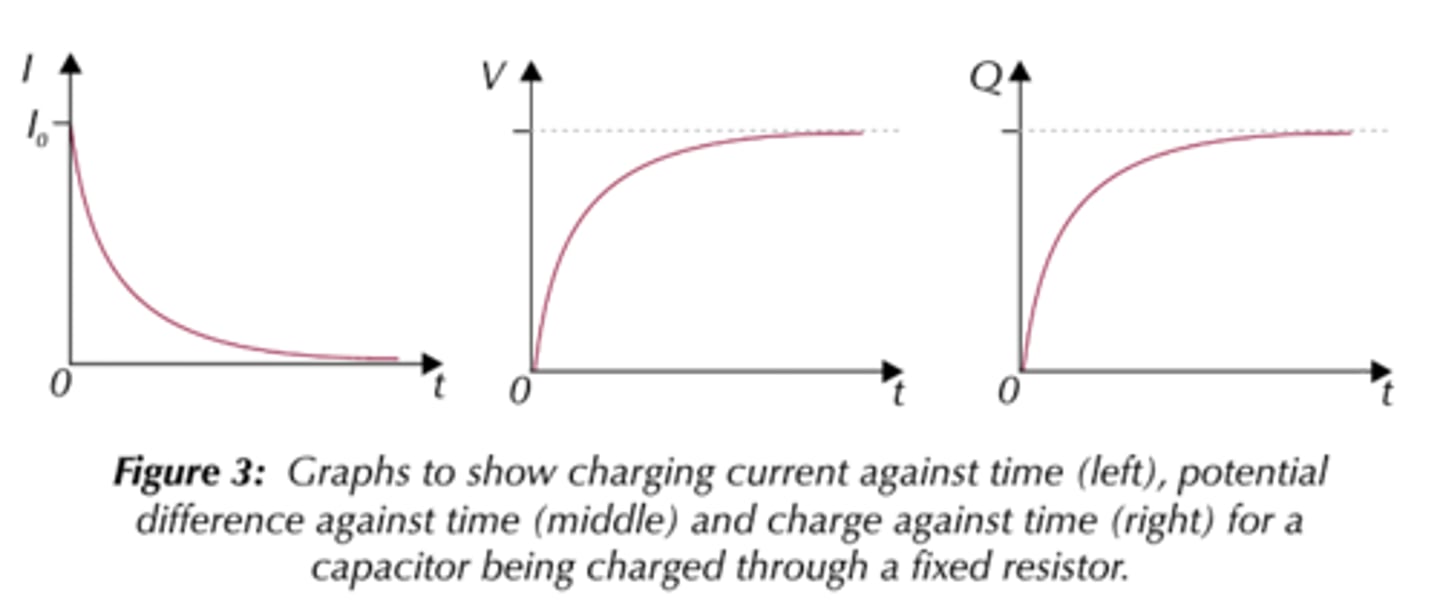
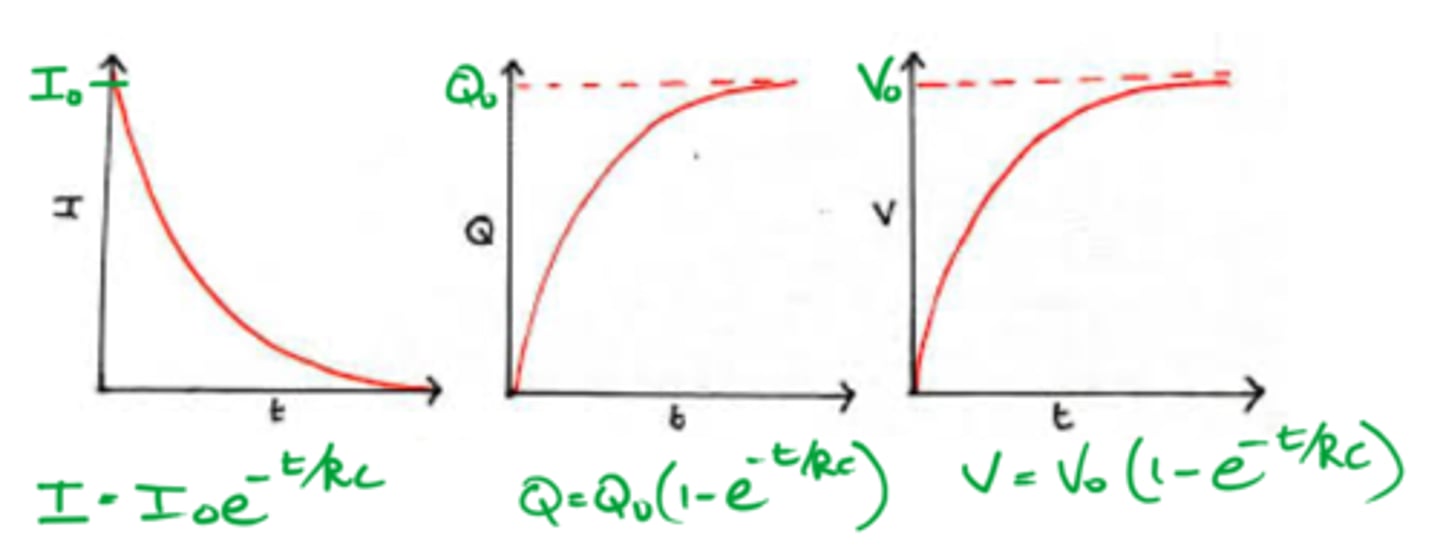
While a capacitor is charging, what will the following graphs look like?

Current v time

p.d. v time

charge stored v time

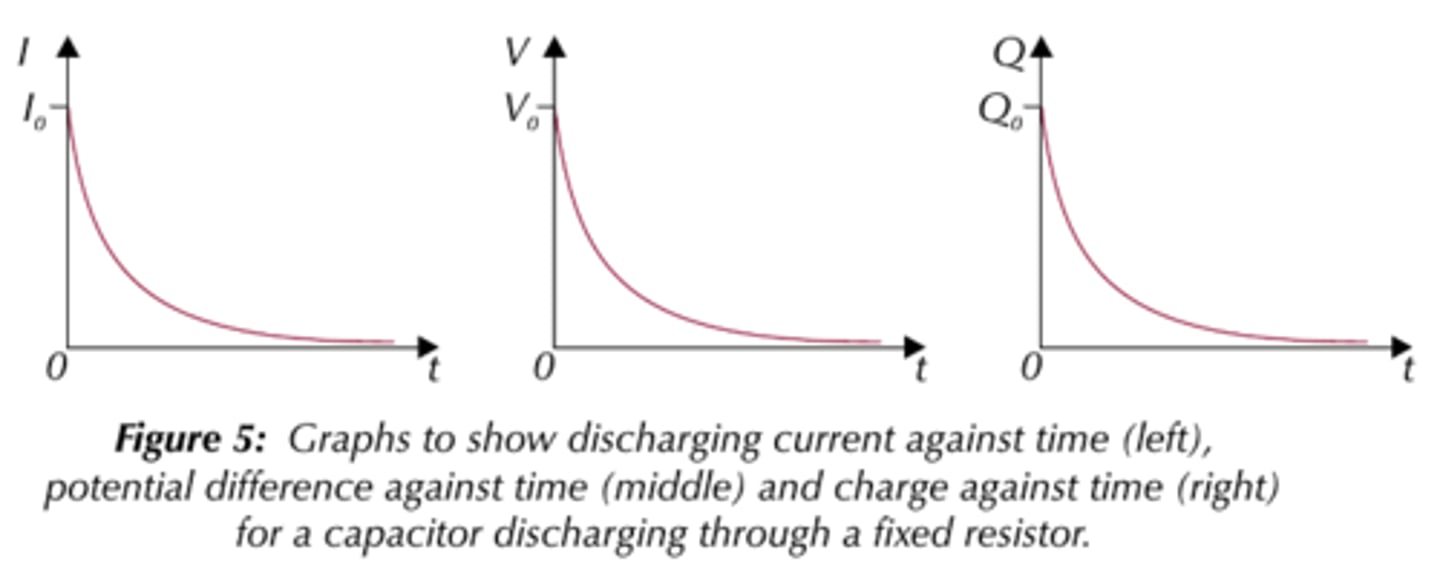
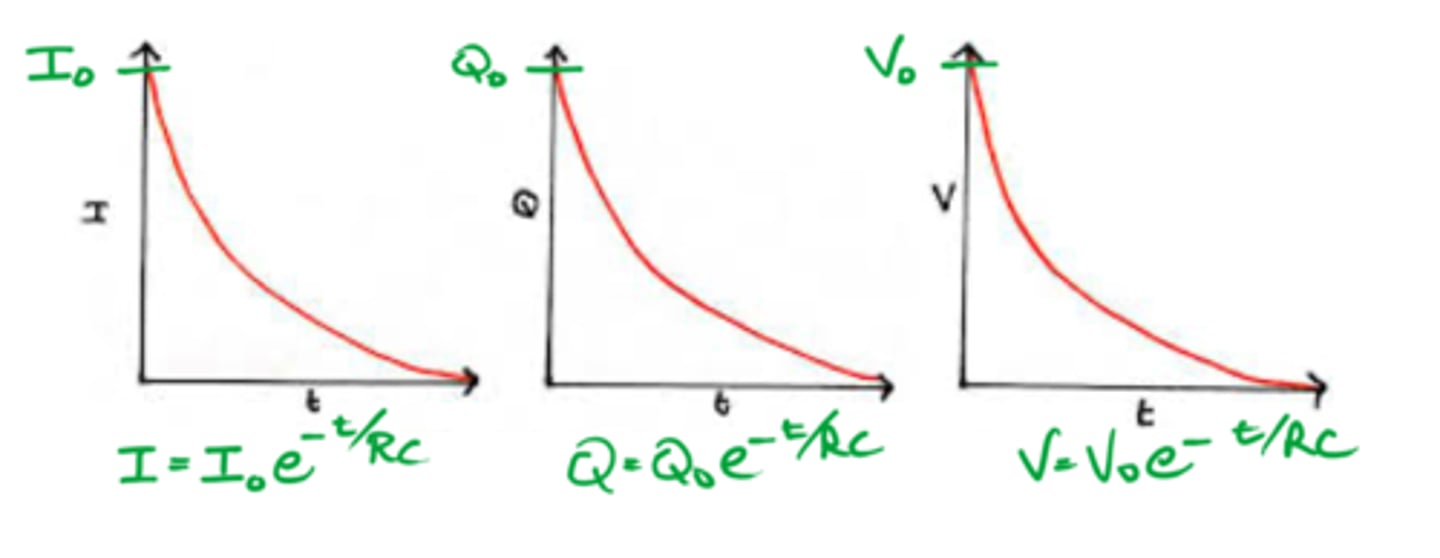
While a capacitor is discharging, what will the following graphs look like?

Current v time

p.d. v time

charge stored v time

What does the area of a I/t graph represent?

What does the gradient of a Q/t graph represent?

What does the gradient of a Q/V graph represent?

What does the area of a V/Q graph represent?

charge (e.g. total charge stored on a capacitor)

current

capacitance

energy stored

Energy stored by a capacitor

e.g. battery with emf ε, charges up capacitor. initially, p.d. of capacitor = ε. the battery is removed and the capacitor discharges through an LED.

1. how much work was done by the battery?

2. how much energy was stored in the capacitor and transferred to the LED?

3. why is this?

4. where does the rest of the energy go?

W = εQ

½εQ

this is because average p.d. over a full charge / discharge is ½ε (it goes from 0 to ε) => work done is ½εQ

dissipates as thermal energy due to resistance in the circuit

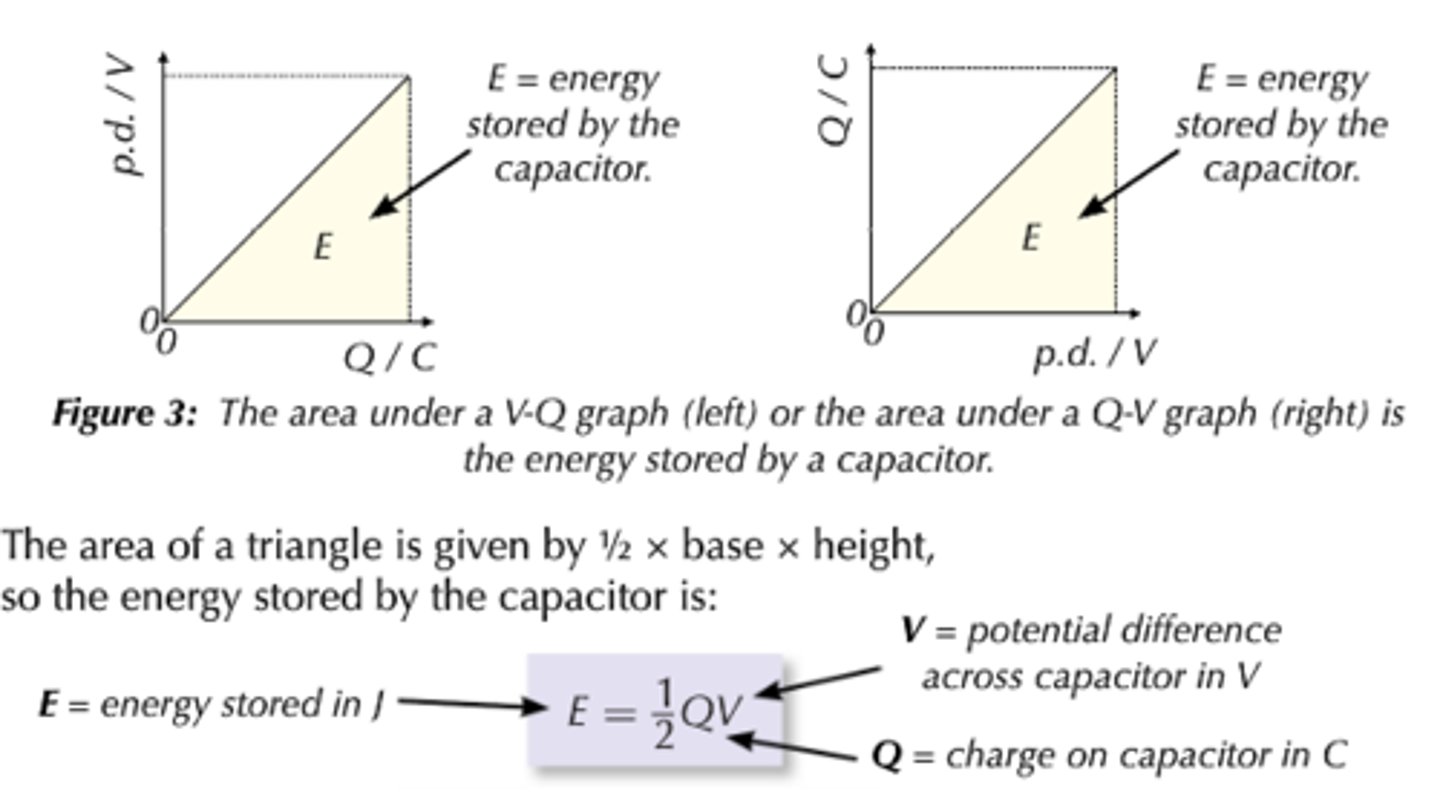
What are the three equations for energy stored by a capacitor?

these are just found from the original E = ½εQ and then rearranging C = Q / V

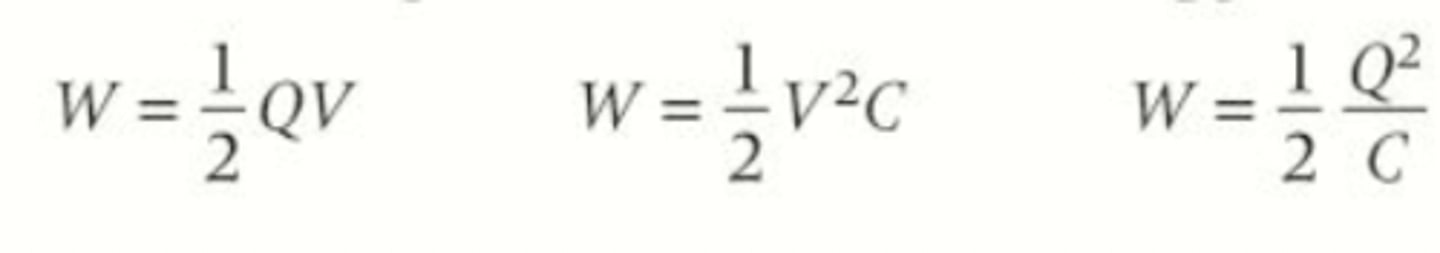
What is permittivity?

What is the permittivity of free space? (in formula book)

= measure of how easy it is to generate an electric field in a material

ε₀ = 8.85 x 10⁻¹² Fm⁻¹

Polar molecules

molecules with uneven charge distribution

this means there is an internal electric field going from positive to negative

Why is increasing the capacitance of a material good?

more charge can be stored per unit volt

=> capacitors can be smaller, or can store more charge in the same area

=> devices can get smaller / charged better

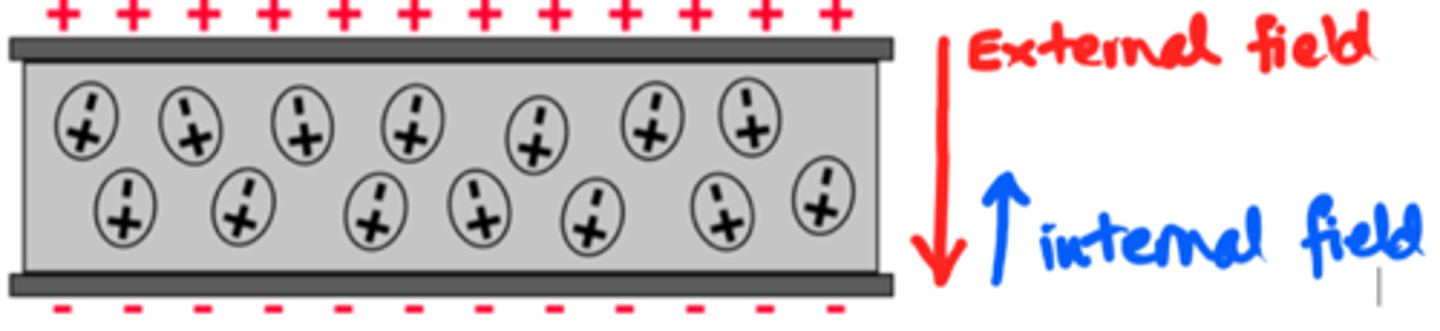
Dielectric

1. what is a dielectric?

2. where are they placed?

3. what is their purpose? and why do they work for this?

an insulator made up of dipolar molecules

placed between the parallel plates to increase capacitance

no ex. e. field => dipolar molecules arranged randomly => no net e. field inside insulator

with ex. e. field, moledules line up against e. field (internal e. field acts in opposite direction)

=> reduced net e. field => E = E(external) - E(internal)

=> E = V / d ∴ V reduced

=> C = Q / V ∴ C increased

Relative permittivity

= ratio of the permittivity of a material to the permittivity of free space

trying to increase this for the dielectric in a capacitor => higher E(internal) => smaller E(external) => larger C

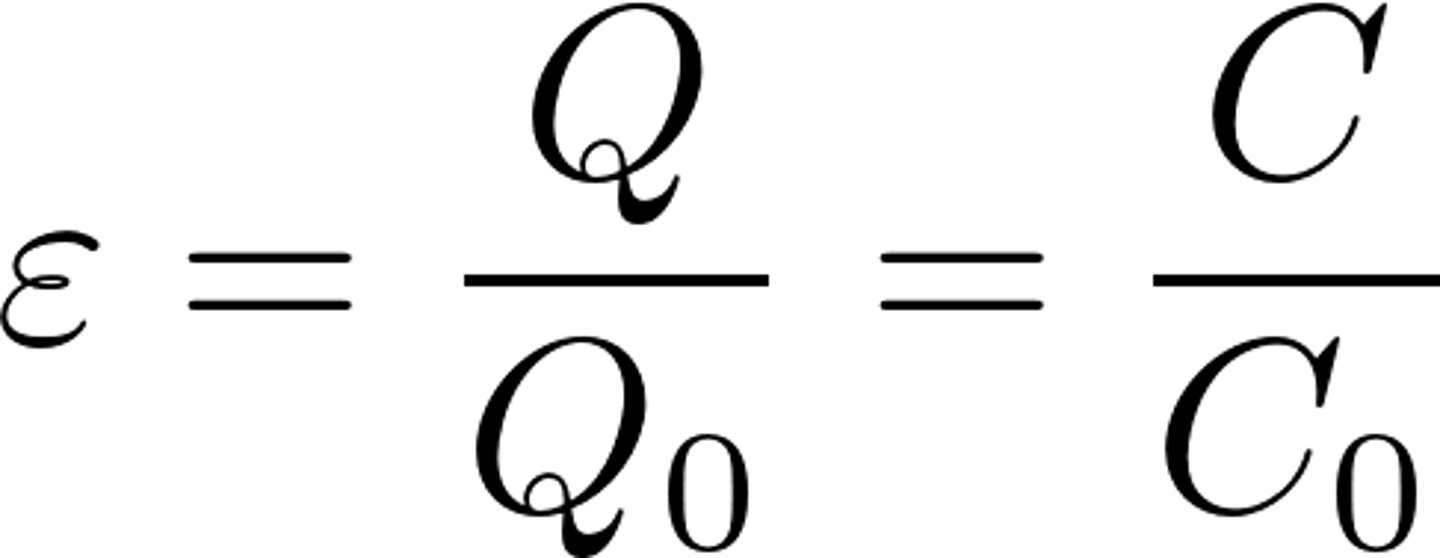
Capacitance equation

A = area of 1 plate

d = distance between plates

ε₀ = permittivity of free space (constant)

εr = relative permittivity of insulator between plates

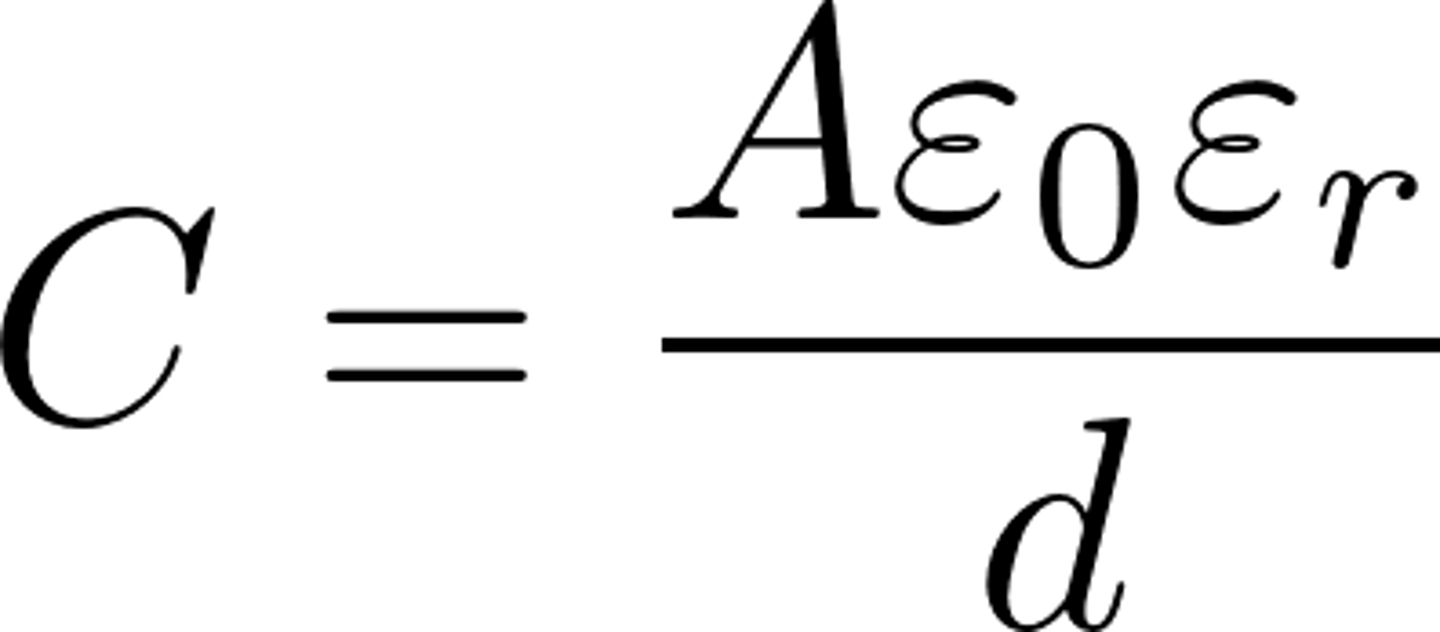
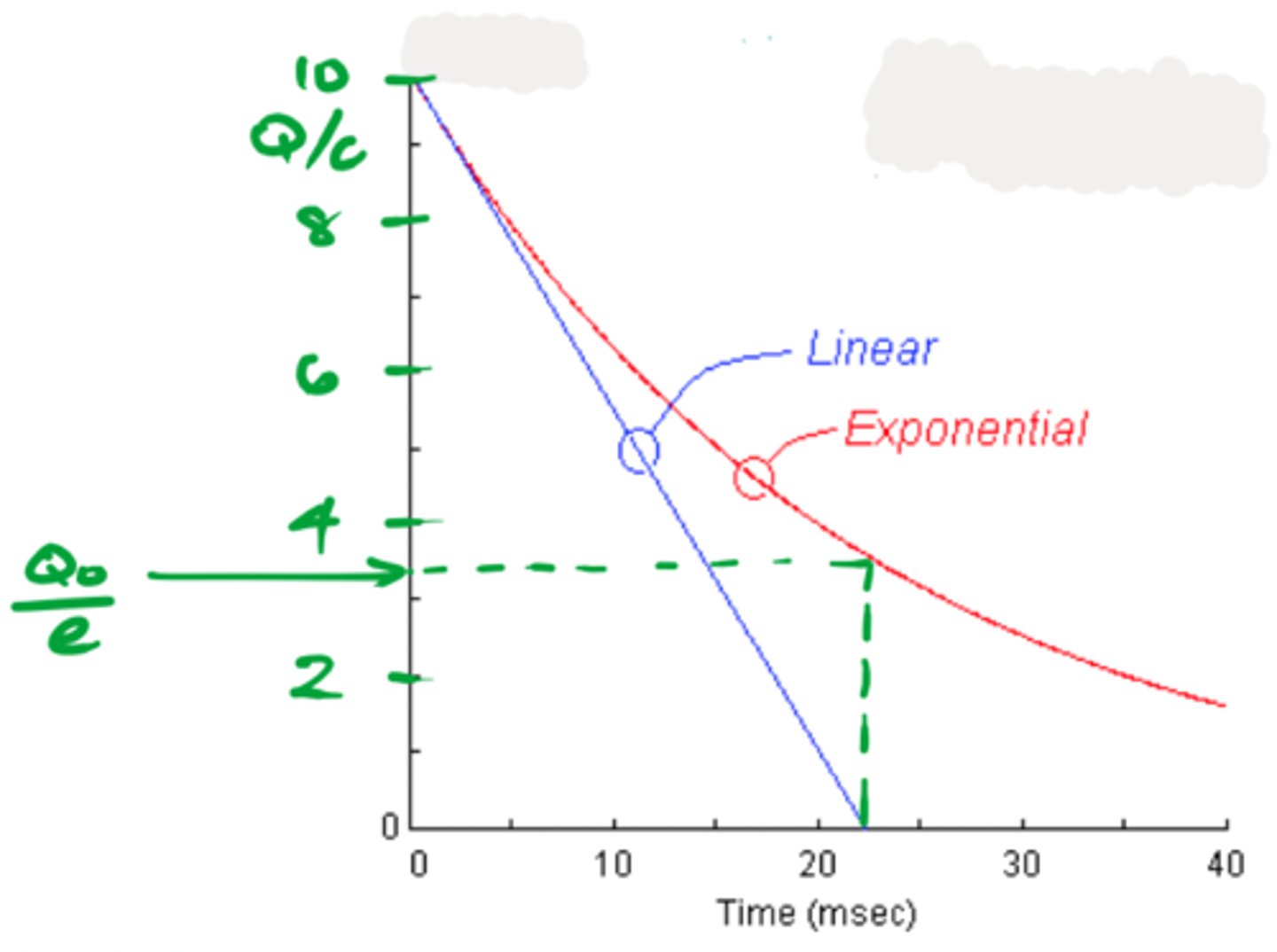
Time constant - definition + equation

time it takes for charge (or voltage, or current) on a capacitor to fall to 1/e (≈ 0.368) of the original charge

T = RC

where T = time constant, R = resistance, C = capacitance

What are the two ways to determine the time constant from a Q/t decay graph?

METHOD 1:

1. look at initial charge / current / voltage

2. find Q₀ / e

3. draw across to determine T

METHOD 2: *provides an estimate only*

1. draw tangent to the curve at t = 0

2. find where this meets the x-axis => T

(as this represents the initial rate of decay => if the capacitor decayed at this constant rate, it would run out of charge after the time constant)

Exponential equations for discharging

Exponential equations for charging

Time to half - definition, equation + derivation

DO HAVE TO KNOW THIS

= time taken for half the charge to decay (or current, or p.d.)

= (RC)ln2

= 0.69 x time constant

can derive this from Q = Q₀e^(-t/RC)

if Q = Q₀ / 2, can find t

What would the capacitance of a metal be?

0 => unable to store charge

What is the definition of magnetic flux density?

What is the symbol? What are the units?

= force per unit length, per unit current on a current-carrying conductor, perpendicular to the conductor

B, Teslas