finding column and null spaces

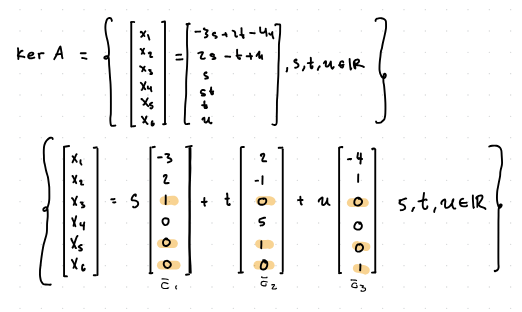
basis for the kernel of A is

the vectors that linearly combine to make the zero vector

dim(ker)A

number of free columns

dim col A

number of leading columns

rank nullity theorem

nullity + rank = # of columns of A

a basis of im A is

the leading columns of A, or those that correspond to leading variables in rref(A)

finding a basis for the span of some vectors

put them as columns of a matrix - the leading columns in ref(A) are a basis

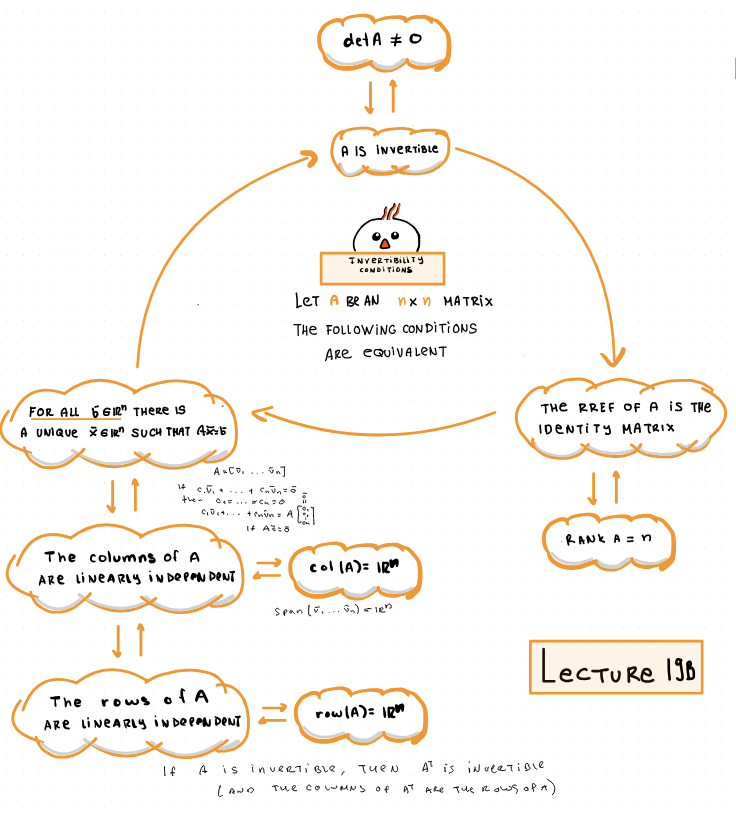
memorize this web