AP Physics Unit13_2: Mirrors

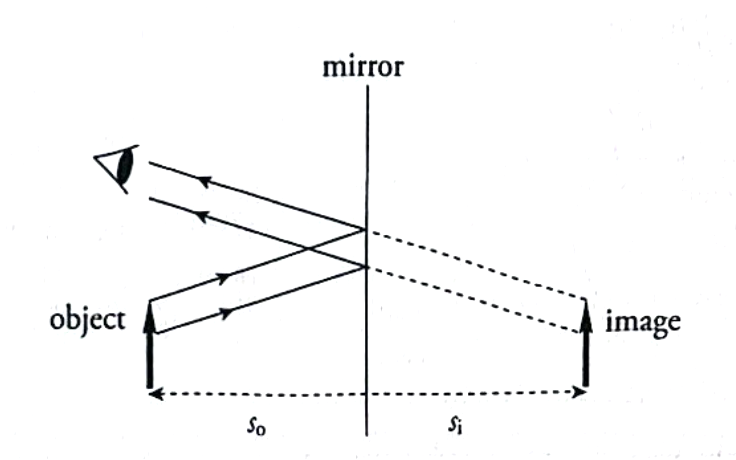
What are the four key properties of images formed by plane mirrors?

1. Location: Image appears behind the mirror at the same distance as the object is in front (|sᵢ| = sₒ).

2. Type: Always virtual (light rays don't actually converge behind the mirror).

3. Orientation: Upright (same vertical direction as the object).

4. Size: Same height as the object (magnification M = 1).

Key Notes:

• Virtual images cannot be projected on a screen.

• The mirror equation confirms this: For a plane mirror (f = ∞), sᵢ = -sₒ and M = 1.

• Used in everyday mirrors (bathroom mirrors, dressing mirrors).

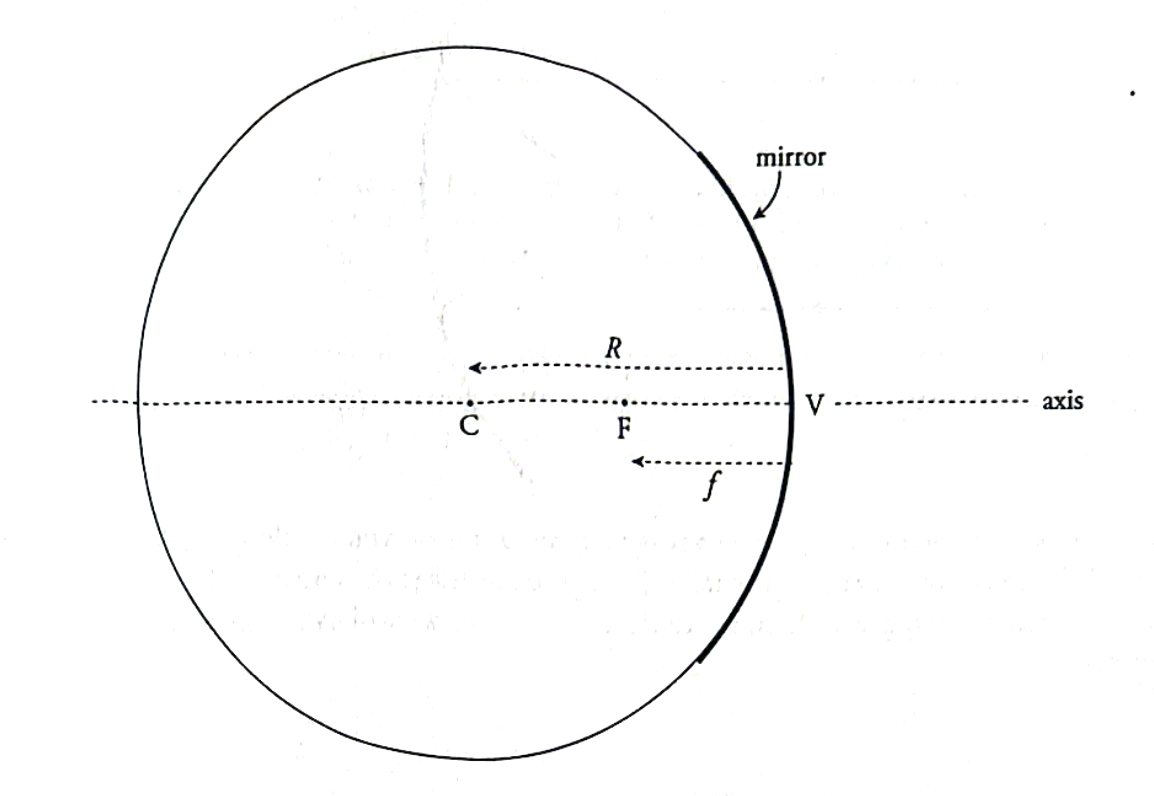
What are the key terms for spherical mirrors (concave & convex)?

• Center of Curvature (C): Center of the sphere the mirror is part of.

• Radius of Curvature (R): Distance from C to the mirror surface.

• Focal Point (F): Where parallel rays converge (concave) or appear to diverge from (convex); f = R/2.

• Vertex (V): Geometric center of the mirror surface.

Key Notes:

• Concave mirrors:

  • f is positive (real focus).

  • Can form real or virtual images depending on object position.

• Convex mirrors:

  • f is negative (virtual focus).

  • Always form virtual, upright, diminished images.

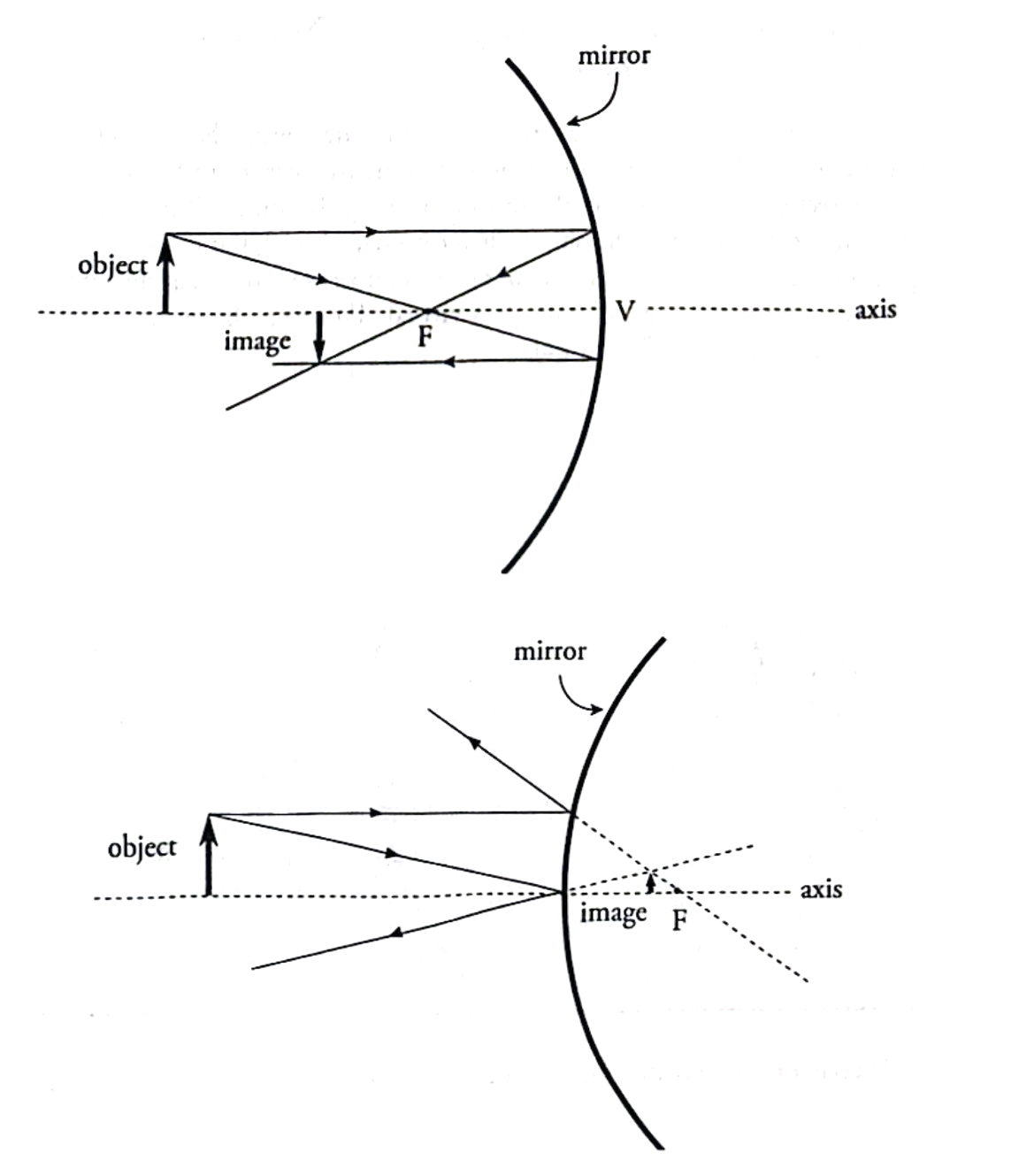
What are the Ray Tracing Rules for concave and convex mirrors?

Concave Mirrors:

1. Parallel to axis → Through F.

2. Through F → Parallel to axis.

3. Through C → Reflects back through C.

Convex Mirrors:

1. Parallel to axis → Diverges as if from F.

2. Toward F → Reflects parallel to axis.

3. Toward C → Reflects back along same path.

Key Notes:

• Only two rays are needed to locate an image.

• Real images form where rays actually intersect (same side as object).

• Virtual images form where rays appear to diverge (opposite side of object).

Mirror Equation & Sign Conventions

How does object position affect images in concave mirrors?

1. Beyond C: Real, inverted, diminished (|M| < 1).

2. At C: Real, inverted, same size (M = -1).

3. Between C and F: Real, inverted, enlarged (|M| > 1).

4. At F: No image (rays parallel).

5. Inside F: Virtual, upright, enlarged (M > 1).

Key Notes:

• Focal point is the threshold:

  • Objects outside F → Real images.

  • Objects inside F → Virtual images.

• Example: Makeup mirrors use the "inside F" case for magnification.

Why do convex mirrors always form virtual images?

• Mathematical proof:

  • f is negative, sₒ is positive → Mirror equation forces sᵢ to be negative.

  • Negative sᵢ → Virtual image.

• Ray-tracing proof:

  • Reflected rays diverge; only virtual images form behind the mirror.

Key Notes:

• Always upright and diminished (|M| < 1).

• Applications: Security mirrors, side-view car mirrors ("objects are closer than they appear").

Example Problem (Concave Mirror)

An object is placed 30 cm from a concave mirror (f = 10 cm). Find the image properties.

Example Problem (Convex Mirror)

An object is placed 20 cm from a convex mirror (f = -30 cm). Find the image properties.

Key Study Tips

1. Draw ray diagrams to visualize image formation.

2. Memorize sign conventions:

   • sₒ: +, f: + (concave) or - (convex), sᵢ: + (real) or - (virtual).

3. Check units: Ensure all distances are in the same units (e.g., cm or m).

Need a mnemonic?

• "Real Is Inverted" (RII): Real images are always Inverted.

• "Convex = Cautious": Convex mirrors make things look smaller (and farther away).