Logarithms and Exponentials

Math Honors 3, this is also for Pre-Calc! I will add more SOON!

Multiplying exponents/powers of the same base.

Add the exponents/powers.

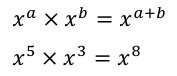
Dividing exponents/powers of the same base.

Subtract the exponents/powers.

Raising to a power with a term with a pre-existing exponent/power.

Multiply the exponents/powers.

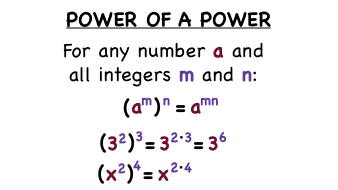
Zero Power

Anything to the power zero is 1

Negative exponents/powers.

Transform the term into a fraction.

Fractional exponents/powers.

The denominator becomes the root and the numerator as the new exponent/power.

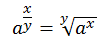
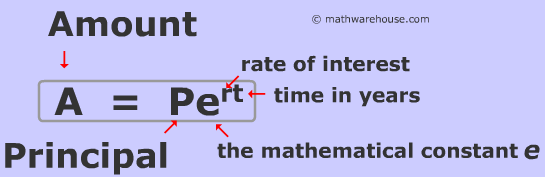
Compound Interest formula.

A = P(1 + r/k)^kt

• A Final Amount

• P Initial amount (also known as principle)

• rInterest rate

• kNumber of times interest is applied (periods)

• t Time

Continuous growth formula.

A = Pe^rt

• A Final Amount

• P Initial amount (principle)

• r Growth rate

• t Time

What is the general form of an exponential function?

f(x) = a ∙ b^x

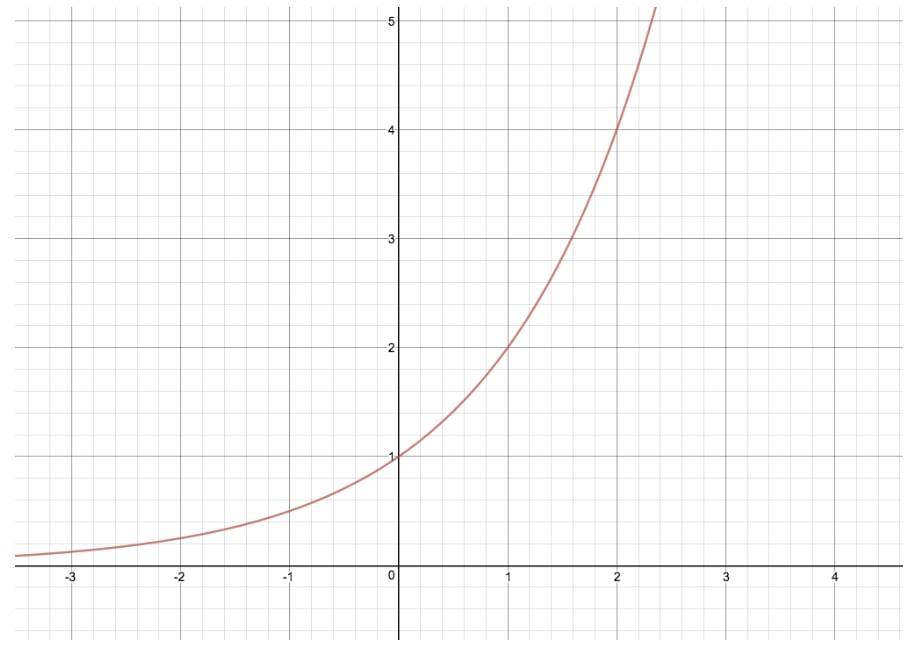
What points (x,y) do ALL exponential functions share?

The point (0,1)

What does a represent in f(x) = a ∙ b^x?

a represents the y-intercept: (0, a)

What does b represent in f(x) = a ∙ b^x?

b represents the common ratio (a common difference)

What do logarithms UNDO?

Logarithms undo powers.

What is the common logarithm?

Logarithmic functions written without a specified base, instead, an invisible 10.

Also referred to as base 10.

What is the natural logarithm?

A Logarithmic function (log) with a base of e. This is written as ln.

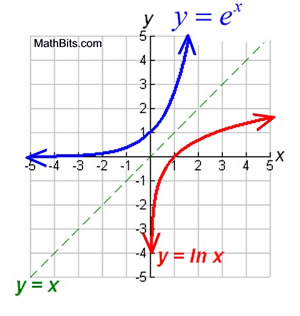
What point (x,y) do ALL log functions share?

The point (1,0).

How could you write the logarithmic equation for y = b^x

log_b y = x OR x = log_b y

What is the restriction for x in y = b^x AND log_b y = x?

None!

What is the restriction for b in y = b^x AND log_b y = x?

b > 0 but b ≠ 1

What is the restriction for y in y = b^x AND log_b y = x?

y > 0