AP Physics 1: Ultimate Guide
Unit 1: Kinematics
Distance and Displacement
Distance and displacement are two important concepts in physics that describe the position of an object in space. While they may seem similar, they have distinct differences.
Distance
- Distance is the total length of the path traveled by an object.
- It is a scalar quantity, meaning it has only magnitude and no direction.
- Distance is measured in units such as meters, kilometers, or miles.
- Distance is not used as much as Displacement in the AP exam, but it is denoted by the letter s or x
Displacement
- Displacement is the change in position of an object from its initial position to its final position.
- It is a vector quantity, meaning it has both magnitude and direction.
- Displacement is measured in units such as meters, kilometers, or miles, and is represented by a vector with an arrow pointing from the initial position to the final position.
Vector and Scalar Quantities
Scalar Quantities
- Scalar quantities are physical quantities that have only magnitude and no direction.
- Examples of scalar quantities include mass, temperature, time, speed, distance, energy, and power.
- Scalar quantities are represented by a single number and are usually measured in units such as kilograms, seconds, meters, and joules.
Vector Quantities
- Vector quantities are physical quantities that have both magnitude and direction.
- Examples of vector quantities include displacement, velocity, acceleration, force, and momentum.
- Vector quantities are represented by a vector, which is a quantity that has both magnitude and direction.
- Vectors are usually represented graphically as arrows, where the length of the arrow represents the magnitude of the vector and the direction of the arrow represents the direction of the vector.
- Vector quantities can be added and subtracted using vector algebra, which takes into account both the magnitude and direction of the vectors.
Position, Velocity, and Acceleration
Position
Position is the location of an object relative to a chosen reference point. It is a vector quantity that can be described using distance and direction. Typically, a coordinate system is used to show where an obejct is located.
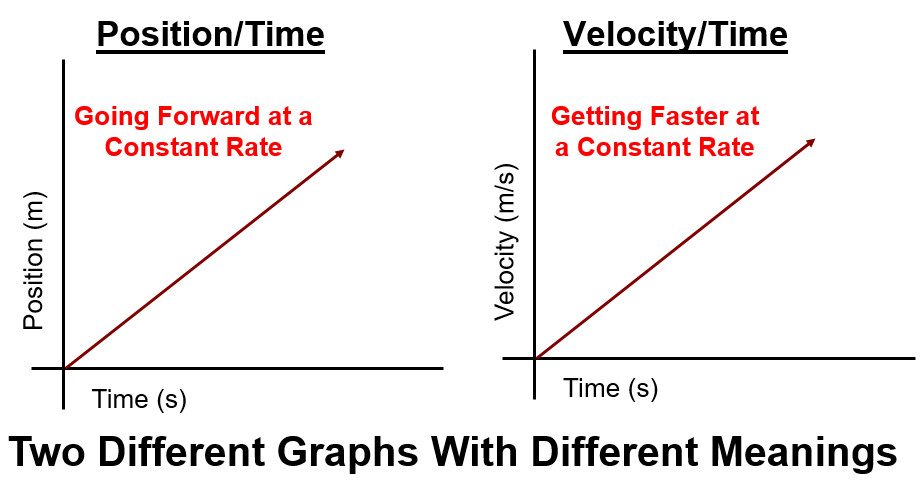
- To determine which way an object is moving look at which way the Position vs Time Graph is sloped
- The slope of a Position vs Time Graph is equal to velocity
- When the slope is a straight line it has constant velocity
- When the slope is a curved lived there is a change in velocity (acceleration)
- When the slope is zero the object is at rest
- The y-intercept is the initial position of the object
Speed vs Velocity
Speed and velocity are both terms used to describe the motion of an object, but they have different meanings.
Speed
Speed is a scalar quantity that refers to how fast an object is moving. It is calculated by dividing the distance traveled by the time taken to travel that distance. The SI unit of speed is meters per second (m/s).
- Scalar quantity
- SI Unit: Meters (m)/Seconds (s)
Equation: S = D/t
Velocity
Velocity is a vector quantity that refers to the rate at which an object changes its position. It is calculated by dividing the displacement of an object by the time taken to travel that displacement. The SI unit of velocity is meters per second (m/s).
- Vector quantity
- SI Unit: Meters (m)/Seconds (s)
Equation: V = x/t
A position vs time graph depicts velocity and a velocity vs time graph depicts acceleration.
Acceleration
Acceleration is the rate of change of velocity with respect to time. It is a vector quantity, which means it has both magnitude and direction. In AP Physics 1, acceleration is an important concept that is used to describe the motion of objects.
Calculating Acceleration
The formula for acceleration is:
a = (v_f - v_i) / t
where a is acceleration, v_f is final velocity, v_i is initial velocity, and t is time.
Units of Acceleration
The SI unit of acceleration is meters per second squared (m/s^2). Other common units of acceleration include feet per second squared (ft/s^2) and kilometers per hour squared (km/h^2).
Positive and Negative Acceleration
When an object is speeding up, its acceleration is positive. When an object is slowing down, its acceleration is negative. If an object is moving in the opposite direction of its acceleration, the acceleration is also negative.
Uniform Acceleration
Uniform acceleration is when an object's acceleration is constant over time. This means that the object's velocity changes by the same amount in each unit of time. The formula for uniform acceleration is:
a = (v_f - v_i) / t = (d/t) / t = d / t^2
where d is the distance traveled.
Non-Uniform Acceleration
Non-uniform acceleration is when an object's acceleration changes over time. This means that the object's velocity changes by different amounts in each unit of time. The formula for non-uniform acceleration is more complex and requires calculus.
Free Fall
Free fall is a special case of uniform acceleration where an object is falling under the influence of gravity. The acceleration due to gravity is approximately 9.8 m/s^2 near the surface of the Earth. The formula for free fall is:
d = (1/2)gt^2
where d is the distance fallen, g is the acceleration due to gravity, and t is time.
Uniformly Accelerated Motion and the BIG FIVE
Uniformly Accelerated Motion
- Uniformly accelerated motion is a type of motion where the acceleration of an object remains constant.
- The velocity of the object changes at a constant rate.
- The acceleration can be positive or negative depending on the direction of the motion.
The BIG FIVE Equations of Motion
- The BIG FIVE equations of motion are a set of equations that describe the motion of an object under uniformly accelerated motion.
- These equations relate the initial velocity, final velocity, acceleration, displacement, and time of an object.
- The equations are:
- v = u + at
- s = ut + 1/2at^2
- v^2 = u^2 + 2as
- s = 1/2(u + v)t
- a = (v - u)/t
- Here,
- u = initial velocity
- v = final velocity
- a = acceleration
- s = displacement
- t = time
Example
- Suppose a car starts from rest and accelerates uniformly at 5 m/s^2 for 10 seconds. Find the final velocity and displacement of the car.
- Using the BIG FIVE equations of motion, we can find:
- v = u + at = 0 + 5*10 = 50 m/s
- s = ut + 1/2at^2 = 010 + 1/25*10^2 = 250 m
- Therefore, the final velocity of the car is 50 m/s and the displacement is 250 m.
Projectile Motion and Angled Motion
Projectile Motion
- Projectile motion is the motion of an object that is thrown or launched into the air and then moves under the influence of gravity.
- The path of a projectile is a parabolic curve.
- The horizontal and vertical components of motion are independent of each other.
- The acceleration due to gravity acts only in the vertical direction.
Equations of Projectile Motion
- The horizontal component of velocity is constant.
- The vertical component of velocity changes due to the acceleration due to gravity.
- The time of flight is the time taken by the projectile to reach the ground.
- The maximum height reached by the projectile is given by the formula:
h = (v₀sinθ)² / 2g - The range of the projectile is given by the formula:
R = v₀²sin2θ / g
Angled Motion
- Angled motion is the motion of an object that is thrown or launched at an angle to the horizontal.
- The path of an angled projectile is a parabolic curve.
- The horizontal and vertical components of motion are dependent on each other.
- The acceleration due to gravity acts in both the horizontal and vertical directions.
Equations of Angled Motion
- The horizontal component of velocity is given by:
v₀cosθ - The vertical component of velocity is given by:
v₀sinθ - gt - The time of flight is given by:
t = 2v₀sinθ / g - The maximum height reached by the projectile is given by:
h = (v₀sinθ)² / 2g - The range of the projectile is given by:
R = v₀²sin2θ / g
Note: v₀ is the initial velocity, θ is the angle of projection, g is the acceleration due to gravity, and t is the time taken.
Unit 2: Dynamics
Dynamics
In AP Physics 1, dynamics is a crucial topic that deals with the study of the causes of motion and changes in motion. It is a fundamental concept that helps us understand the behavior of objects and systems in the physical world. Dynamics involves the application of Newton's laws of motion, which are the backbone of classical mechanics. These laws explain how forces affect the motion of an object and how the motion of an object affects the forces acting upon it.
Newton's Laws of Motion
First Law: Law of Inertia
This law is also referred as The Law of Inertia because it explains the tendency of objects to resist changes in their state of motion. For example, an object at rest will remain at rest, and an object in motion will continue to move in a straight line at a constant speed, unless acted upon by an external force. This law is particularly important in understanding the behavior of moving objects, such as planets, satellites, and even cars.
- An object at rest will remain at rest, and an object in motion will remain in motion with a constant velocity, unless acted upon by a net external force.
- Inertia is the tendency of an object to resist changes in its motion.
Gravitational vs Inertial Mass
Gravitational Mass
Gravitational Mass is determined by the strength of the gravitational force experienced by the body. Gravitational Mass is measured by comparing the force of gravity of an unknown mass to the force of gravity of a known mass hence the equation:
F= G*m1m2/r^2
- Gravitational mass is the measure of the strength of the gravitational force experienced by an object when it is placed in a gravitational field.
- It is the mass that determines the strength of the gravitational attraction between two objects.
- Gravitational mass is measured by comparing the weight of an object to a known standard mass under the influence of gravity.
Inertial Mass
Inertial mass is found my applying a known force to an unknown mass, and applying a = F/M hence the formula:
a = F/m
- Inertial mass is the measure of an object's resistance to a change in its state of motion.
- It is the mass that determines the force required to accelerate an object.
- Inertial mass is measured by applying a known force to an object and measuring its resulting acceleration.
Second Law: Law of Acceleration
Newton’s second law predicts what will happen if an unbalanced force does not act on an object which is that the object will accelerate. Precisely, his law states that the objects acceleration a, will be directly proportional to the strength of the total force Fnet and inversely proportional to the object’s mass, m.
a = F/M
Fnet = ma or ΣF = ma
- The acceleration of an object is directly proportional to the net external force acting on the object, and inversely proportional to its mass.
- F = ma, where F is the net external force, m is the mass of the object, and a is its acceleration.
Third Law: Law of Action-Reaction
Newton’s Third Law states, “For every action, there is an equal and opposite reaction.” This means that in every interaction between forces, there is ALWAYS a pair or forces action on the same object. The magnitude of each force is the same keeping the object balanced and in equilibrium. Forces always come in pair - equal and opposite action - reaction force pairs.
- For every action, there is an equal and opposite reaction.
- Whenever one object exerts a force on a second object, the second object exerts an equal and opposite force on the first object.
- When two bodies interact, they exert forces on each other. These forces are equal in magnitude and opposite in direction.
- Force pairs always act in opposite directions, but they do not always cancel each other out.
Limitations and Applications of Newton's Laws
- Projectile motion: the motion of an object that is launched into the air and then moves under the influence of gravity.
- Circular motion: the motion of an object that moves in a circular path.
- Friction: the force that opposes motion between two surfaces that are in contact.
- Tension: the force that is transmitted through a string, rope, cable or wire when it is pulled tight by forces acting from opposite ends.
- Newton's laws are only valid in inertial reference frames.
- Newton's laws do not apply to objects that are moving at speeds close to the speed of light.
- Newton's laws do not take into account the effects of quantum mechanics.
Key Information for Gravity and Forces
- Gravity: Two bodies with mass attract each other and exert gravitational forces.
- Normal Force: A surface exerts an upward force on a body to balance the downward force of gravity.
- Tension: A rope or string pulled tight exerts a force on connected objects.
- Compression: A rope or string pushed together exerts a force on connect objects.
- Friction: Two surfaces rubbing against each other exert a force that resists relative motion.
- Applied Force: A force applied to a body causes the body to exert a force in the opposite direction.
Understanding the different types of forces and how they interact with each other is crucial in many fields, including physics, engineering, and even everyday life. By analyzing the forces at play in a given situation, we can predict how objects will move and interact with each other, and design systems and structures that are safe and efficient. These are some important forces to know for the AP Physics 1 exam, and it can help you with many MCQs and FRQs.
Unit 3: Circular Motion and Gravitation
Uniform Circular Motion
Uniform circular motion is the motion of an object moving in a circular path at a constant speed. In this type of motion, the object's velocity is constantly changing due to the change in direction of its motion. You should remember that although the speed may be constant, the velocity is not because the direction is always changing meaning that the velocity is always changing. Since the velocity is changing, there must be acceleration. The acceleration does not change the speed of the object, rather it changes the direction of the velocity to keep the object moving along the circular path.
Centripetal Force and Acceleration
Centripetal force is the force that acts on an object moving in a circular path, directed towards the center of the circle. It is responsible for keeping the object moving in a circular path. The centripetal acceleration is what turns the velocity vectors to keep the object traveling in a circle. The magnitude of the centripetal acceleration depends on the object’s speed, v, and the radius of the circular path, r,
a꜀ = v^2/r
where a꜀ is the centripetal acceleration, v is the velocity of the object, and r is the radius of the circle.
- The centripetal force required to keep an object moving in a circular path is given by the formula:
- F = ma = mv^2 / r
- where F is the centripetal force, m is the mass of the object, v is the velocity of the object, and r is the radius of the circle.
Some examples of uniform circular motion include the motion of a car around a circular track, the motion of a satellite orbiting the Earth, and the motion of a ball on a string being swung in a circle.
Gravitational and Electric Forces
The four fundamental forces in physics are the gravitational force, the electromagnetic force, the weak force, and the strong force. Gravity dominates at the largest mass and distance scales because its effects are proportional to the mass of the objects involved.
Gravitational Force
The gravitational force is the force of attraction between two masses. It is one of the weakest forces in nature, but it dominated at large mass and distances. An example of this is our solar system where the huge gravitational pull of the sun keep the planets in orbit.
- Attractive force between two objects with mass
- Proportional to the product of their masses and inversely proportional to the square of the distance between them
- Described by Newton's Law of Universal Gravitation: F = G * (m1 * m2) / r^2
- G is the gravitational constant (6.674 * 10^-11 N * m^2 / kg^2)
Electric Force
- Attractive or repulsive force between two charged objects
- Proportional to the product of their charges and inversely proportional to the square of the distance between them
- Described by Coulomb's Law: F = k * (q1 * q2) / r^2
- k is the Coulomb constant (9 * 10^9 N * m^2 / C^2)
Gravitational Acceleration
Gravitational acceleration is the acceleration experienced by an object due to the force of gravity. It is denoted by the symbol 'g' and is measured in meters per second squared (m/s^2). The gravitational force is always acting vertically downward towards the center of a planet. If this is the only force that is being exerted on an object at a specific time, then the object is considered to be in free fall.
Formula
The formula for gravitational acceleration is:
g = G * M / r^2
where:
- G is the gravitational constant (6.674 * 10^-11 N * m^2 / kg^2)
- M is the mass of the object causing the gravitational force
- r is the distance between the object and the center of mass of the other object
On Earth, the value of gravitational acceleration is approximately 9.81 m/s^2. This means that an object in free fall near the surface of the Earth will accelerate at a rate of 9.81 m/s^2. The variable g, or the gravitational field is subject to change based on the planet itself or the object’s location relative to the planet’s surface. On Earth, we know g as 9.8 m/s^2, but on other planets, the value is different.
F₉ = m1a
Gm1m2/r^2 = m1a
a = gm/r^2
g = Gm/r^2
Unit 4: Energy
Work and Mechanical Energy
Work
When you lift a dumbbell from the floor, you exert a force on it over a distance, and when you push a box across a floor, you also exert a force on it over a distance. The application of force over a distance is called work. Work is a scalar quantity and is measured in units of J (joules).
- Work is the transfer of energy that occurs when a force is applied over a distance.
- The formula for work is W = Fd, where W is work, F is force, and d is distance.
- Work is measured in joules (J).
Work at an Angle
The previous formula only works when work is done completely parallel to the intended distance of travel. When the force is done at an angle, the formula becomes:
W = Fd cos θ
Example: A force is applied to a block at an angle of 30 degrees to the horizontal. The force has a magnitude of 50 N and the block is displaced by 2 meters in the direction of the force. Using the equation that relates work, force, displacement and the angle between the force and displacement, we can find the work done on the block, which is equal to the force times the displacement times the cosine of the angle between them. Thus, the work done on the block is 86.6 J.
Mechanical Energy
- Mechanical energy is the sum of kinetic energy and potential energy in a system.
- Kinetic energy is the energy of motion and is given by the formula KE = 1/2mv^2, where m is mass and v is velocity.
- Potential energy is the energy stored in an object due to its position or configuration and is given by the formula PE = mgh, where m is mass, g is acceleration due to gravity, and h is height.
- Mechanical energy is conserved in a closed system, meaning that the total amount of mechanical energy remains constant.
Work-Energy Theorem
- The work-energy theorem states that the net work done on an object is equal to the change in its kinetic energy.
- The formula for the work-energy theorem is Wnet = ΔKE, where Wnet is the net work done on an object and ΔKE is the change in its kinetic energy.
- The work-energy theorem can be used to calculate the work done on an object or the change in its kinetic energy.
Wtotal = deltaK
The work-energy theorem begins to answer the question by stating that a system gains or loses Kinetic Energy by transferring it to through work between the environments.
Conservation of Mechanical Energy
- In a closed system, the total amount of mechanical energy is conserved.
- This means that the sum of kinetic energy and potential energy remains constant.
- The conservation of mechanical energy can be used to solve problems involving the motion of objects in a system.
The sum of an object’s kinetic energy and potential energies is called its total mechanical energy
E = K + U
Ki + Ui = Kf + Uf
This is the simplest form of the Law of Conservation on Total Energy.
Conservation of Energy with Nonconservative Forces
The equation Ki + Ui = Kf + Uf holds if no nonconservative forces are doing work. However, if work is done by such forces during the process under investigation, then the equation needs to be modified to account for this work as follows:
Ki + Ui + Wother= Kf + Uf
Example Questions:
Suppose a block of mass 2 kg is placed on a rough surface with an initial velocity of 5 m/s. The coefficient of kinetic friction between the block and the surface is 0.2. The block comes to rest after covering a distance of 10 m. Find the work done by frictional force.
Power
Power is the rate at which work is done or energy is transferred. It is a scalar quantity and is measured in watts (W). Power is the rate at which energy is transferred into, or out of, within a system,.
Formula
The formula for power is:
P = W/t
where P is power, W is work, and t is time.
Units
The SI unit for power is watts (W), which it was originally (Joules/s) later renamed the watt. Other common units include horsepower (hp) and kilowatts (kW).
Calculations
To calculate power, you need to know the amount of work done and the time it took to do it. For example, if a person lifts a 50 kg weight 2 meters in 5 seconds, the work done is:
W = mgh
W = (50 kg)(9.8 m/s^2)(2 m)
W = 980 J
The power can then be calculated using the formula:
P = W/t
P = 980 J / 5 s
P = 196 W
Therefore, the power output of the person lifting the weight is 196 watts.
Power and Energy
Power and energy are related, but they are not the same thing. Energy is the ability to do work, while power is the rate at which work is done. The amount of energy used depends on both the power and the time it is used for. For example, a 100 W light bulb left on for 10 hours uses more energy than a 50 W light bulb left on for the same amount of time.
Power and Efficiency
Efficiency is a measure of how much of the input energy is converted into useful output energy. The efficiency of a device can be calculated using the formula:
efficiency = useful output energy / input energy
Power is also related to efficiency. The higher the power output of a device, the more energy it can convert into useful work. However, a device with a high power output may not necessarily be more efficient than a device with a lower power output.
Unit 5: Momentum
What is momentum?
Momentum is the degree of an object's opposition to a modification in motion. It is a vector quantity, indicating it has both size and direction. The momentum formula is p = mv, where p is momentum, m is mass, and v is velocity. This unit accounts for 12-18% of the exam weight.
Momentum and Impulse
Momentum
Momentum is a measure of an object’s resistance to a change in motion, which is defined as the product of an object’s mass and velocity. It has both magnitude and direction.
- Momentum is a property of a moving object that is equal to the product of its mass and velocity.
- It is a vector quantity, meaning it has both magnitude and direction.
- The unit of momentum is kg m/s.
- The formula for momentum is:
p = mv, where p is momentum, m is mass, and v is velocity. - Momentum is conserved in a closed system, meaning the total momentum of the system before a collision is equal to the total momentum after the collision.
Impulse
Impulse is the change in momentum of an object over a given time period. It is the product of the force applied to an object and the time over which the force is applied.
- Impulse is the change in momentum of an object over a period of time.
- It is also a vector quantity.
- The unit of impulse is Ns (newton-second).
- The formula for impulse is:
J = FΔt, where J is impulse, F is the force applied, and Δt is the time interval over which the force is applied. - Impulse is equal to the area under a force-time graph.
Conservation of Linear Momentum
Linear momentum is the product of mass and velocity of an object. According to the law of conservation of linear momentum, the total momentum of a system of objects remains constant if no external forces act on the system. This means that the sum of the momenta of all the objects in the system before a collision is equal to the sum of the momenta of all the objects after the collision.
- This law is applicable to both elastic and inelastic collisions.
- In an elastic collision, the total kinetic energy of the system is conserved, while in an inelastic collision, some of the kinetic energy is converted into other forms of energy, such as heat or sound.
- The conservation of linear momentum is a fundamental principle in physics and is used to explain a wide range of phenomena, from the behavior of subatomic particles to the motion of planets in the solar system.
- This law is also used in engineering and technology to design and analyze systems that involve the transfer of momentum, such as rockets, satellites, and automobiles.
- The conservation of linear momentum is a consequence of the fundamental symmetry of nature known as translational symmetry, which states that the laws of physics are the same in all inertial reference frames.
The total linear momentum of an isolated ststem remains constant.
total Pinital = total Pfinal
Collisions
Collisions occur when two or more objects come into contact with each other. The following are some important concepts related to collisions:
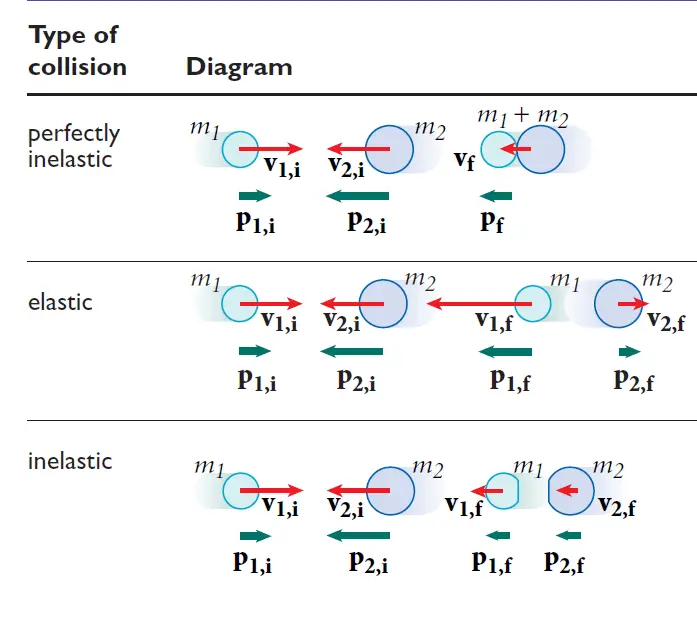
Types of Collisions
There are three types of collisions:
- Elastic Collisions: In an elastic collision, the total kinetic energy of the system is conserved. This means that the objects bounce off each other without losing any energy.
- Inelastic Collisions: In an inelastic collision, the total kinetic energy of the system is not conserved. This means that the objects stick together after the collision and some energy is lost as heat or sound.
- Perfectly Inelastic Collision: In an Perfectly Inelastic Collision, the objects stick together and travel in the same direction.
The image below represents these three types:
Collisions are an important concept in physics and have many real-world applications. Understanding the types of collisions, conservation of momentum, coefficient of restitution, and impulse can help in analyzing and predicting the behavior of objects in collisions.
Unit 6: Simple Harmonic Motion
Simple Harmonic Motion
Simple Harmonic Motion (SHM) is a type of periodic motion where the restoring force is directly proportional to the displacement from the equilibrium position and is drected towards it.
- The motion is periodic and repetitive.
- The acceleration is directly proportional to the displacement and is always directed towards the equilibrium position.
- The velocity is maximum at the equilibrium position and minimum at the extreme positions.
- The displacement, velocity, and acceleration are all sinusoidal functions of time.
- The period of oscillation is independent of the amplitude.
Examples of SHM include: A mass attached to a spring and oscillating vertically or a A pendulum swinging back and forth.
Displacement: x = A cos(ωt + φ)
Velocity: v = -Aω sin(ωt + φ)
Acceleration: a = -Aω^2 cos(ωt + φ)
where A is the amplitude, ω is the angular frequency, t is the time, and φ is the phase angle.
Energy in SHM
The total mechanical energy of a system undergoing SHM is constant and is the sum of kinetic and potential energy.
- Total energy: E = 1/2 kA^2
- Kinetic energy: K = 1/2 mv^2
- Potential energy: U = 1/2 kx^2
where k is the spring constant, m is the mass, v is the velocity, and x is the displacement.
Force and Amplitude
Force in Simple Harmonic Motion
Since the block is acceleration and deceleration, there must be some force that is making it do so. This this cause, the spring exerts a force on the block.
- It is a vector quantity, meaning it has both magnitude and direction.
- The SI unit of force is Newton (N).
- Force can cause an object to accelerate, change direction, or deform.
F = -kx
Also known as Hooke’s Law, the k is the called the spring constant and tells us how strong the spring is. The greater the K, the stiffer the spring actually is.
Amplitude
- Amplitude is a measure of the magnitude of a wave.
- It is the maximum displacement of a particle from its equilibrium position in a wave.
- Amplitude is measured in meters (m) for a mechanical wave and in volts (V) for an electromagnetic wave.
- The amplitude of a wave determines its intensity and energy.
- The amplitude of a wave can also affedct th eforc e.
Period and Frequency
Period
- The period of a wave is the time it takes for one complete cycle of the wave to occur.
- It is denoted by the symbol T and is measured in seconds (s).
- The period is inversely proportional to the frequency of the wave.
- Mathematically, T = 1/f, where f is the frequency of the wave.
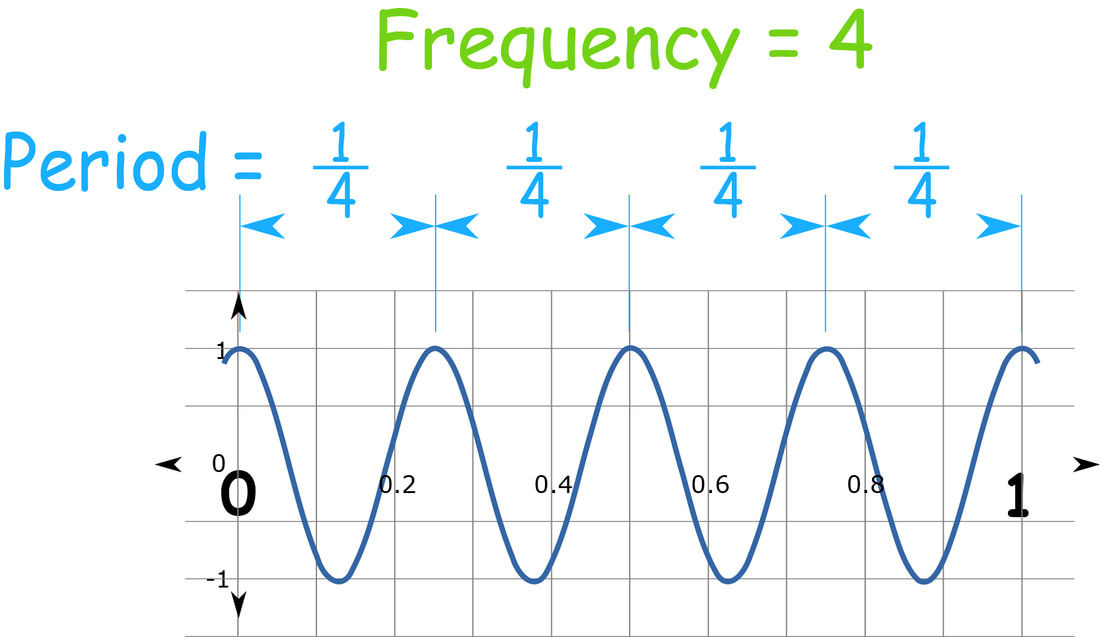
Frequency
The frequency of a wave is the number of complete cycles of the wave that occur in one second.
It is denoted by the symbol f and is measured in Hertz (Hz).
The frequency is directly proportional to the energy of the wave.
Mathematically, f = 1/T, where T is the period of the wave.
Pendulums
In a system, if the spring is used the period will increase with objects mass and decrease with as a greater spring constant increases. This is because a mass will resist acceleration and a large spring constant will make the spring exert more force.
- Object's mass affects the period of the spring, not the pendulum
- Mass can act as either inertial or gravitational
- Gravitational mass accelerates due to the force of gravity between it and the Earth
- All objects fall at the same rate due to gravitational mass
- Inertial mass is not pushed by gravity but by external forces like the spring force
- Inertial mass can accelerate at different rates depending on the force applied
Pendulums are a common topic in AP Physics Unit 7, which covers simple harmonic motion. A pendulum is a weight suspended from a pivot point that swings back and forth due to gravity. The period of a pendulum (the time it takes to complete one full swing) is determined by the length of the pendulum and the acceleration due to gravity. The equation for the period of a pendulum is T=2π√(L/g), where T is the period, L is the length of the pendulum, and g is the acceleration due to gravity. Pendulums are used in many applications, such as clocks and seismometers.
Unit 7: Rotational Motion
Rotational Motion
Rotational motion is the motion of an object around an axis or a fixed point. It is also known as circular motion. In rotational motion, an object rotates about an axis, which may or may not pass through the object. If we recall previously, an object’s mass measures its inertia. The greater the inertia on an object, the harder it is to change its velocity which means the greater the inertia, greater the force to move an object.
| Linear Kinematics | Rotational Kinematics |
|---|---|
| Force | Torque |
| Mass | Moment of Inertia |
| Acceleration | Angular Acceleration |
| Fnet = ma | Tnet = Ia |
| Velocity | Angular Velocity |
- Angular displacement: The angle through which an object rotates.
- Angular velocity: The rate of change of angular displacement with respect to time.
- Angular acceleration: The rate of change of angular velocity with respect to time.
- Moment of inertia: The resistance of an object to rotational motion.
- Torque: The force that causes an object to rotate about an axis.
Rotational motion is important in many areas of physics and engineering, including: Mechanics, Astronomy and Robotics
Rotational Kinematics
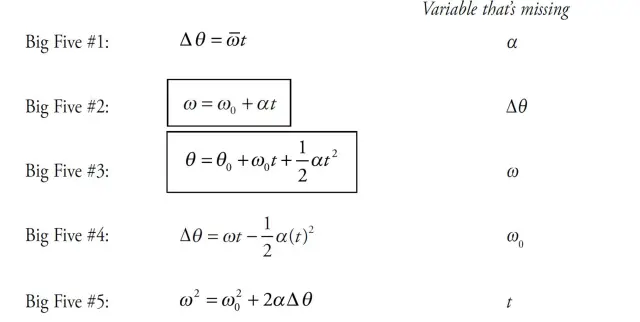
Rotational kinematics is the study of motion of objects that rotate around a fixed axis. Like linear equations, we use rotational equations to determine the same factors. The formulas just differ slightly but are essentially the same concept with different variables and used in different ways.
Angular Displacement
Angular displacement is the change in the angle of rotation of an object. It is measured in radians and is denoted by the symbol "theta" (θ). The formula for angular displacement is:
θ = (s / r)
where s is the arc length and r is the radius of the circle.
Angular Velocity
Angular velocity is the rate of change of angular displacement. It is measured in radians per second and is denoted by the symbol "omega" (ω). The formula for angular velocity is:
ω = (θ / t)
where t is the time taken for the angular displacement.
Angular Acceleration
Angular acceleration is the rate of change of angular velocity. It is measured in radians per second squared and is denoted by the symbol "alpha" (α). The formula for angular acceleration is:
α = (ωf - ωi) / t
where ωf is the final angular velocity, ωi is the initial angular velocity, and t is the time taken for the change in angular velocity.
Relationship between Linear and Angular Motion
There is a relationship between linear and angular motion. The linear velocity of a point on a rotating object is equal to the product of the angular velocity and the radius of the circle. The formula for linear velocity is:
v = rω
Similarly, the linear acceleration of a point on a rotating object is equal to the product of the angular acceleration and the radius of the circle. The formula for linear acceleration is:
a = rα
Center of Mass
The center of mass (COM) is the point in an object or system that moves as if all the mass were concentrated at that point. It is the average position of all the parts of the system, weighted according to their masses.
- The center of mass of an object or system is always located within the object or system itself.
- The center of mass of a symmetrical object is located at the geometric center of the object.
- The center of mass of an object or system can be outside the object or system if the mass is distributed unevenly.
- The motion of an object or system can be described as if all the mass were concentrated at the center of mass.
- The center of mass of a system is conserved in the absence of external forces.
Calculating the Center of Mass
The center of mass of a system can be calculated using the following formula:
COM = (m1r1 + m2r2 + … + mn rn) / (m1 + m2 + … + mn)
where m is the mass of each part of the system and r is the distance of each part from a chosen origin.
Torque
Torque is a measure of the twisting force that causes rotation. It is a vector quantity, which means it has both magnitude and direction. The magnitude of torque is given by the product of force and the perpendicular distance from the axis of rotation to the line of action of the force.
The direction of torque is given by the right-hand rule. If the fingers of the right hand are curled in the direction of rotation, then the thumb points in the direction of torque.
Formula
The formula for torque is:
τ = r x F
where τ is the torque, r is the distance from the axis of rotation to the line of action of the force, and F is the force. The SI unit of torque is the newton-meter (N·m). In the US customary system, the unit of torque is the foot-pound (ft·lb).