Unit 6: Simple Harmonic Motion

Simple Harmonic Motion

Simple Harmonic Motion (SHM) is a type of periodic motion where the restoring force is directly proportional to the displacement from the equilibrium position and is drected towards it.

The motion is periodic and repetitive.
The acceleration is directly proportional to the displacement and is always directed towards the equilibrium position.
The velocity is maximum at the equilibrium position and minimum at the extreme positions.
The displacement, velocity, and acceleration are all sinusoidal functions of time.
The period of oscillation is independent of the amplitude.

Examples of SHM include: A mass attached to a spring and oscillating vertically or a A pendulum swinging back and forth.

Displacement: x = A cos(ωt + φ)

Velocity: v = -Aω sin(ωt + φ)

Acceleration: a = -Aω^2 cos(ωt + φ)

where A is the amplitude, ω is the angular frequency, t is the time, and φ is the phase angle.

Energy in SHM

The total mechanical energy of a system undergoing SHM is constant and is the sum of kinetic and potential energy.

Total energy: E = 1/2 kA^2
Kinetic energy: K = 1/2 mv^2
Potential energy: U = 1/2 kx^2

where k is the spring constant, m is the mass, v is the velocity, and x is the displacement.

Force and Amplitude

Force in Simple Harmonic Motion

Since the block is acceleration and deceleration, there must be some force that is making it do so. This this cause, the spring exerts a force on the block.

It is a vector quantity, meaning it has both magnitude and direction.
The SI unit of force is Newton (N).
Force can cause an object to accelerate, change direction, or deform.

F = -kx

Also known as Hooke’s Law, the k is the called the spring constant and tells us how strong the spring is. The greater the K, the stiffer the spring actually is.

Amplitude

Amplitude is a measure of the magnitude of a wave.
It is the maximum displacement of a particle from its equilibrium position in a wave.
Amplitude is measured in meters (m) for a mechanical wave and in volts (V) for an electromagnetic wave.
The amplitude of a wave determines its intensity and energy.
The amplitude of a wave can also affedct th eforc e.

Period and Frequency

Period

The period of a wave is the time it takes for one complete cycle of the wave to occur.
It is denoted by the symbol T and is measured in seconds (s).
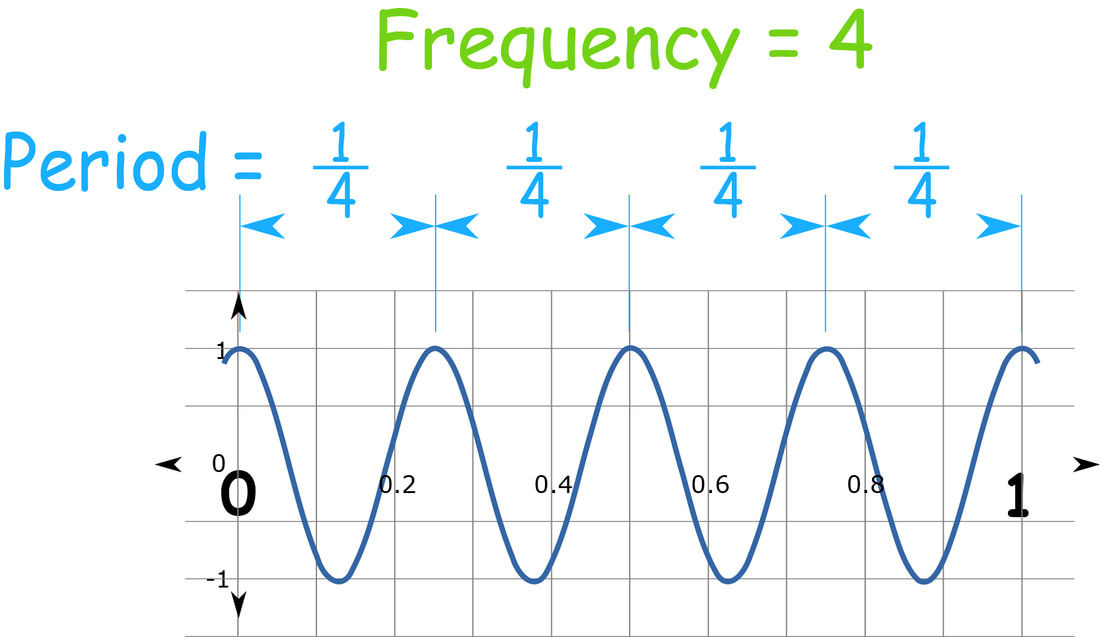
The period is inversely proportional to the frequency of the wave.
Mathematically, T = 1/f, where f is the frequency of the wave.

Frequency

The frequency of a wave is the number of complete cycles of the wave that occur in one second.
It is denoted by the symbol f and is measured in Hertz (Hz).
The frequency is directly proportional to the energy of the wave.
Mathematically, f = 1/T, where T is the period of the wave.

Pendulums

In a system, if the spring is used the period will increase with objects mass and decrease with as a greater spring constant increases. This is because a mass will resist acceleration and a large spring constant will make the spring exert more force.

Object's mass affects the period of the spring, not the pendulum
Mass can act as either inertial or gravitational
Gravitational mass accelerates due to the force of gravity between it and the Earth
All objects fall at the same rate due to gravitational mass
Inertial mass is not pushed by gravity but by external forces like the spring force
Inertial mass can accelerate at different rates depending on the force applied

Pendulums are a common topic in AP Physics Unit 7, which covers simple harmonic motion. A pendulum is a weight suspended from a pivot point that swings back and forth due to gravity. The period of a pendulum (the time it takes to complete one full swing) is determined by the length of the pendulum and the acceleration due to gravity. The equation for the period of a pendulum is T=2π√(L/g), where T is the period, L is the length of the pendulum, and g is the acceleration due to gravity. Pendulums are used in many applications, such as clocks and seismometers.

Note