Unit 7: Torque and Rotational Motion
Rotational Motion
Rotational motion is the motion of an object around an axis or a fixed point. It is also known as circular motion. In rotational motion, an object rotates about an axis, which may or may not pass through the object. If we recall previously, an object’s mass measures its inertia. The greater the inertia on an object, the harder it is to change its velocity which means the greater the inertia, greater the force to move an object.
| Linear Kinematics | Rotational Kinematics |
|---|---|
| Force | Torque |
| Mass | Moment of Inertia |
| Acceleration | Angular Acceleration |
| Fnet = ma | Tnet = Ia |
| Velocity | Angular Velocity |
- Angular displacement: The angle through which an object rotates.
- Angular velocity: The rate of change of angular displacement with respect to time.
- Angular acceleration: The rate of change of angular velocity with respect to time.
- Moment of inertia: The resistance of an object to rotational motion.
- Torque: The force that causes an object to rotate about an axis.
Rotational motion is important in many areas of physics and engineering, including: Mechanics, Astronomy and Robotics
Rotational Kinematics
Rotational kinematics is the study of motion of objects that rotate around a fixed axis. Like linear equations, we use rotational equations to determine the same factors. The formulas just differ slightly but are essentially the same concept with different variables and used in different ways.
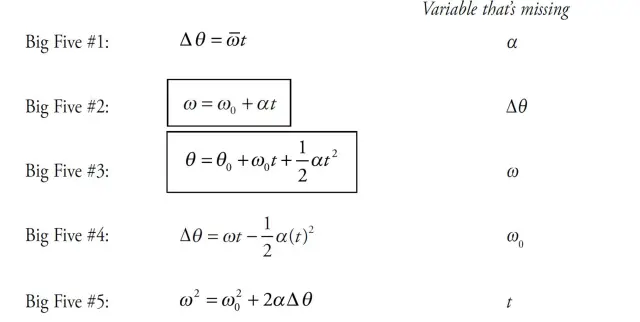
Angular Displacement
Angular displacement is the change in the angle of rotation of an object. It is measured in radians and is denoted by the symbol "theta" (θ). The formula for angular displacement is:
θ = (s / r)
where s is the arc length and r is the radius of the circle.
Angular Velocity
Angular velocity is the rate of change of angular displacement. It is measured in radians per second and is denoted by the symbol "omega" (ω). The formula for angular velocity is:
ω = (θ / t)
where t is the time taken for the angular displacement.
Angular Acceleration
Angular acceleration is the rate of change of angular velocity. It is measured in radians per second squared and is denoted by the symbol "alpha" (α). The formula for angular acceleration is:
α = (ωf - ωi) / t
where ωf is the final angular velocity, ωi is the initial angular velocity, and t is the time taken for the change in angular velocity.
Relationship between Linear and Angular Motion
There is a relationship between linear and angular motion. The linear velocity of a point on a rotating object is equal to the product of the angular velocity and the radius of the circle. The formula for linear velocity is:
v = rω
Similarly, the linear acceleration of a point on a rotating object is equal to the product of the angular acceleration and the radius of the circle. The formula for linear acceleration is:
a = rα
Center of Mass
The center of mass (COM) is the point in an object or system that moves as if all the mass were concentrated at that point. It is the average position of all the parts of the system, weighted according to their masses.
- The center of mass of an object or system is always located within the object or system itself.
- The center of mass of a symmetrical object is located at the geometric center of the object.
- The center of mass of an object or system can be outside the object or system if the mass is distributed unevenly.
- The motion of an object or system can be described as if all the mass were concentrated at the center of mass.
- The center of mass of a system is conserved in the absence of external forces.
Calculating the Center of Mass
The center of mass of a system can be calculated using the following formula:
COM = (m1r1 + m2r2 + … + mn rn) / (m1 + m2 + … + mn)
where m is the mass of each part of the system and r is the distance of each part from a chosen origin.
Torque
Torque is a measure of the twisting force that causes rotation. It is a vector quantity, which means it has both magnitude and direction. The magnitude of torque is given by the product of force and the perpendicular distance from the axis of rotation to the line of action of the force.
The direction of torque is given by the right-hand rule. If the fingers of the right hand are curled in the direction of rotation, then the thumb points in the direction of torque.
Formula
The formula for torque is:
τ = r x F
where τ is the torque, r is the distance from the axis of rotation to the line of action of the force, and F is the force. The SI unit of torque is the newton-meter (N·m). In the US customary system, the unit of torque is the foot-pound (ft·lb).