Коллоквиум по алгебре

2 курс 4 модуль

Дайте определение прямого произведения групп

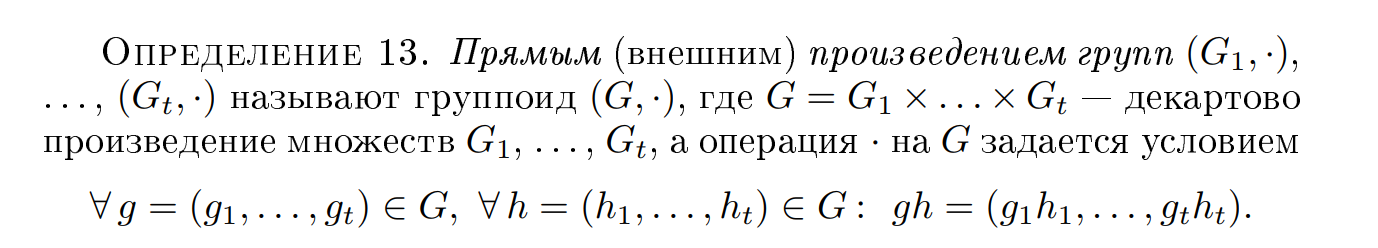
Если G - прямое произведение групп. G - группа?

Да

Если G - прямое произведение групп. Когда G - абелева?

тогда и только тогда, когда G1,…,Gi - абелевы

G - прямое произведение групп. Чему равен порядок элемента g из этой группы?

Порядок g равен НОК порядков элементов g1,…,gi

G - прямое произведение групп. Чему равна экспонента группы G?

НОК(expG1,…,expGi)

G1,…,Gt - конечные циклические группы порядков, соответственно, m1, …, mt и G - прямое произведение этих групп. Что можно сказать о группе G?

Следующие утверждения эквивалентны:
1) G - циклическая группа
2) m1,…,mt попарно взаимно просты

Дайте определение прямого произведения подгрупп

Пусть группа H раскладывается в прямое произведение подгрупп H1…Ht. Чему равен порядок элемента h из группы H?

НОК(ord h1,…, ord ht)

Пусть группа H раскладывается в прямое произведение подгрупп H1…Ht. Чему равна экспонента группы H?

НОК(exp H1, … exp Ht)

Пусть группа H раскладывается в прямое произведение подгрупп H1…Ht. Чему равен порядок группы H?

|H|=|H1|*…*|Ht|

Пусть группа H раскладывается в прямое произведение подгрупп H1…Ht. Чему изоморфна группа H?

H изоморфна прямому произведению групп H1…Ht

Пусть H_1,…,H_t - подгруппы группы H. При каком условии H - прямое произведение этих подгрупп?

Если H_1,…,H_t поэлементно перестановочны, т.е. h_i h_j = h_j h_i, \forall h_i \in H_i, \forall h_j \in H_j, \forall i≠ j

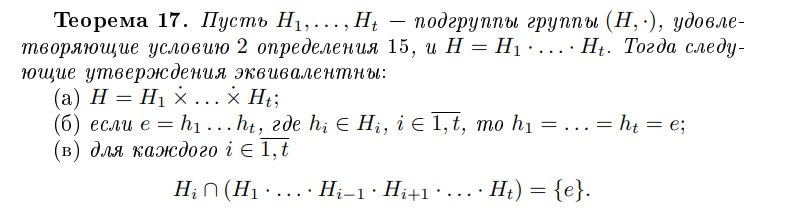
Пусть H раскладывается в прямое произведение подгрупп H_1,…,H_t

Чему равна единица в группе H?

если e=h_1 … h_t, h_i \in H_i, то h_1=…=h_t=e

Пусть H раскладывается в прямое произведение подгрупп H_1,…,H_t

Чему равно пересечение H_i и H_1 \cdot … \cdot H_{i-1} \cdot H_{i+1} \cdot … \cdot H_t?

{e}

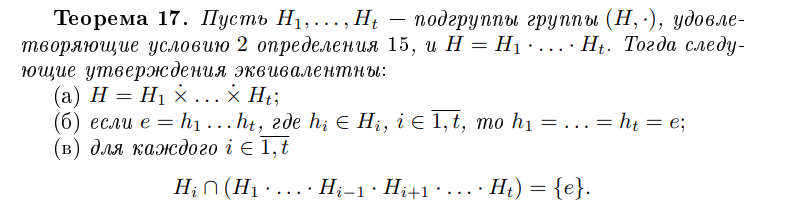
Дайте определение разложимой группы

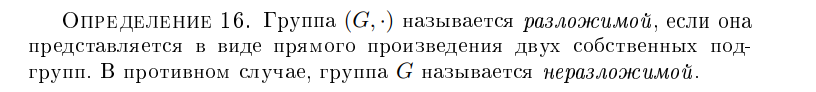
Дайте определение неразложимой группы

Группа G называется простой

Если \forall H < G, \forall K < G:G=HK - прямое произведение \Rightarrow H,K - несобственные подгруппы G

Дайте определение примарной группы.

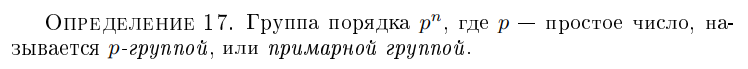
Когда циклическая группа G разложима?

Когда она конечна и непримарна

Когда циклическая группа G неразложима?

Тогда и только тогда, когда она бесконечна или примарна

Во что раскладывается конечная, непримарная, циклическая группа G?

Раскладывается однозначно, с точностью до перестановки слагаемых, в прямую сумма примарных циклических подгрупп.

G раскладывается в прямое произведение подгрупп H и K. Что можно сказать про подгруппы H и K?

H и K нормальны в G

Дайте определение простой группы

Группа G называется простой
Если \forall H < G, \forall K < G:G=HK - прямое произведение \Rightarrow H,K - несобственные подгруппы G

Лемма Коши

Если G - абелева группа порядка m и p - простой делитель m, то в G существует подгруппа порядка p.

Теорема Лагранжа

Порядок подгруппы H конечной группы G делит порядок G и

|G|=|G:H|\cdot|H|

Дайте определение силовской p-подгруппы

Первая теорема Силова

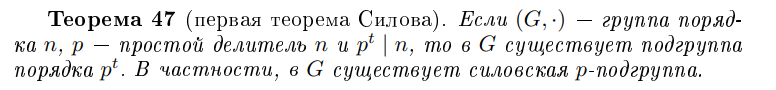
Вторая теорема Силова

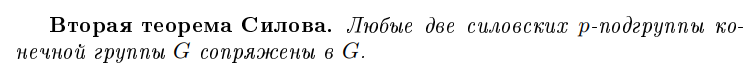
Третья теорема Силова

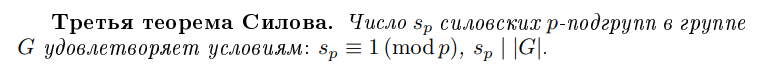
Во что раскладывается конечная непримарная абелева группа G?

Критерий простоты конечной абелевой группы

Конечная абелева группа простая \iff она примарна

Дайте определения: тип разложения, каноническое разложение

Любая конечная абелева группа либо сама является циклической примарной, либо раскладывается в прямое произведение примарных циклических подгрупп: G= < g_1 > + … + < g_t > , ord g_i = p_{i}^{k_i}, p_1,…,p_t - простые числа

Если в этом разложении слагаемые упорядочены так, что
(p_{i} \geq p_{i+1}) \ and \ ((p_i = p_{i+1}) \Rightarrow (k_i \geq k_{i+1})), то это каноническое разложение конечной абелевой группы G, а вектор (p_{1}^{k_1},…,p_{t}^{k_t}) называется типом этого разложения.

Дайте определение:
тип абелевой группы

Типом группы называется тип канонического разложения этой группы

Дайте определение

Векторное пространство

Дайте определение

Линейной выражение вектора из векторного пространства

Дайте определение

Линейной выражение системы векторов из векторного пространства через другую систему векторов этого пространства

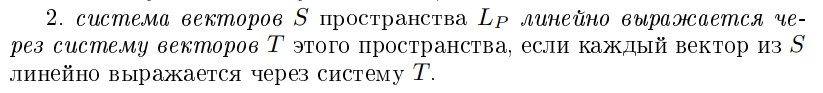
Дайте определение

Линейно зависимая система векторов

Критерий линейной зависимости

Когда система, состоящая из одного вектора линейно зависима?

тогда и только тогда, когда этот вектор нулевой

Когда система из двух векторов линейно зависима?

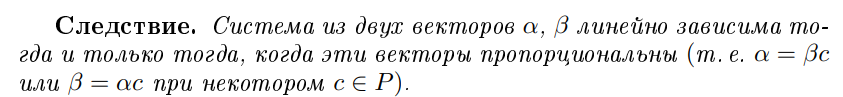
Что можно сказать про систему векторов, если какая-то ее подсистема линейно зависима?

Она тоже линейно зависима

Что можно сказать про подсистемы линейно независимой системы векторов?

Любая подсистема линейно независима

Когда система векторов линейно зависима, если она состоит из >1 вектора и первый вектор ненулевой?

Если добавить в линейно независимую систему векторов еще один вектор, когда новая система будет линейно независима?

Дайте определение

Линейно зависимая бесконечная система векторов

Дайте определение

Базис системы векторов, базис векторного пространства

Какая система векторов имеет базис?

Любая

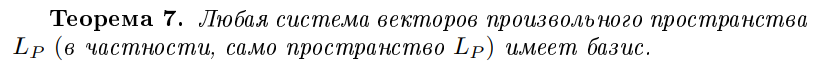
Сколько есть способов линейного выражения вектора в векторном пространстве?

Если выражается, то одним способом

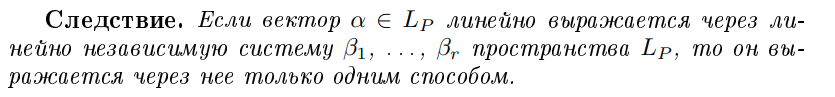
Дайте определение

Линейное отображение

Дайте определение

Матрица смены базиса

Дайте определение

Матрица линейного преобразования

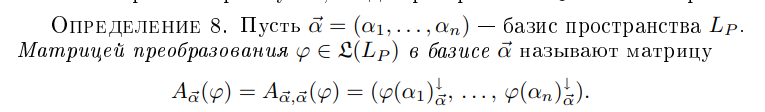
Дайте определение

Собственный вектор преобразования

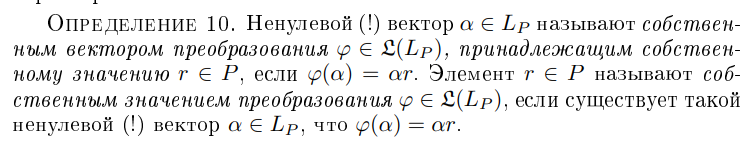
Дайте определение

Собственное значение линейного преобразования

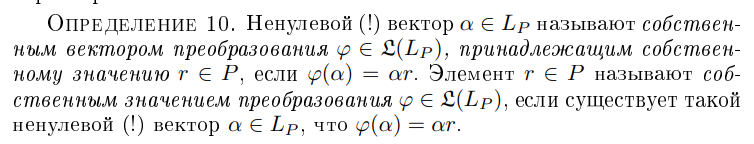
Дайте определение

Кольцо

Дайте определение

Делитель нуля

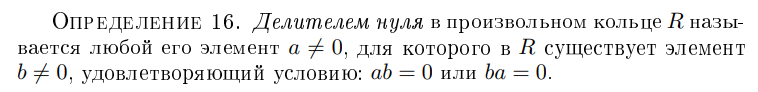
Дайте определение

Область целостности

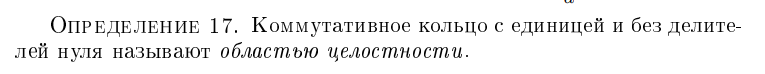
Дайте определение

Поле

Дайте определение

Тело

Тело - кольцо с единицей, отличной от нуля, в котором каждый ненулевой элемент обратим

Есть ли делители нуля в поле?

нет

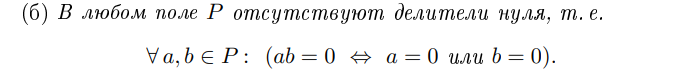
Если в кольце R есть элемент a ≠ 0, не являющийся делителем нуля, что тогда можно сказать о кольце R?

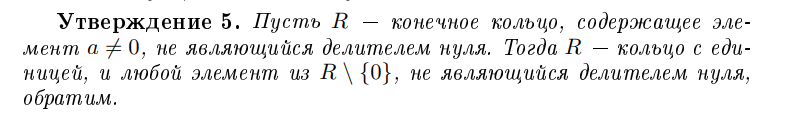
Когда кольцо R является полем?

Тогда и только тогда, когда в R нет делителей нуля

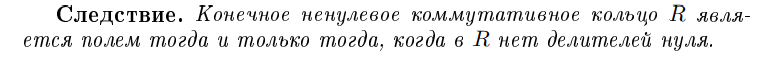
Дайте определение

Характеристика кольца

Чему равна характеристика кольца с единицей?

Дайте определение

Идеал кольца

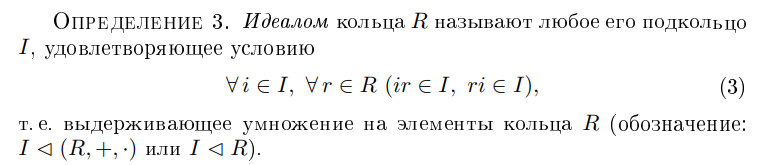
Если I - идеал, а L - подкольцо кольца R,
что можно сказать про I+L?

это подольцо кольца R

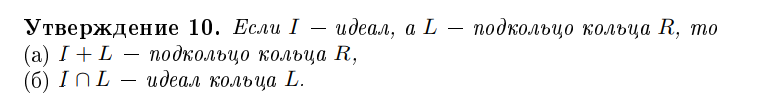
Если I - идеал, а L - подкольцо кольца R,
что можно сказать про I \cap L?

это идеал кольца L

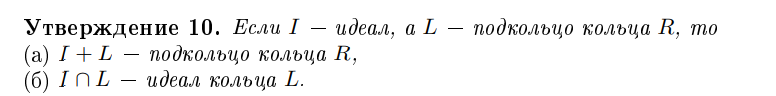
Если I, J - идеалы кольца R,
что можно сказать про I + L?

это идеал кольца R

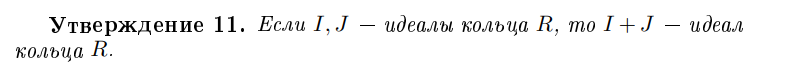
Дайте определение

Главный идеал

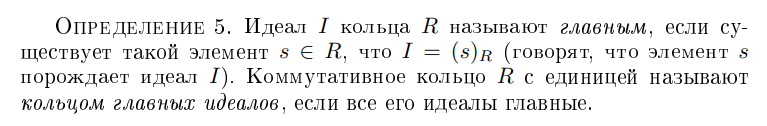
Дайте определение

Кольцо главных идеалов

Кольцо - КГИ, если любой его идеал главный

Приведите пример КГИ

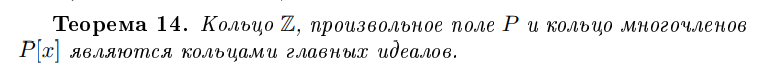
Является ли \mathbb{Z} КГИ?

Да

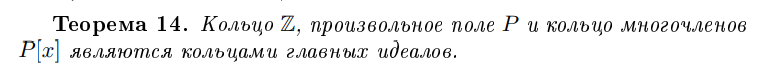
Является ли произвольное поле P КГИ?

Да

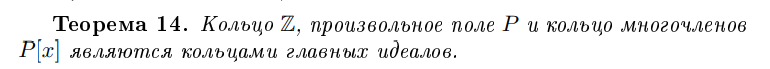
Является ли кольцо многочленов КГИ?

Да

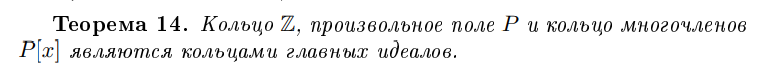
Дайте определение

Простое кольцо

Когда коммутативное кольцо R≠0 является простым?

Когда коммутативное кольцо R≠0 является полем?

Когда коммутативное кольцо R с единицей является полем?

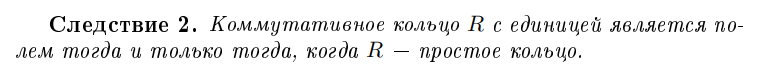
Дайте определение
Фактор-кольцо

Фактор-кольцо - фактор-группа по идеалу кольца

R - кольцо с единицей, I - идеал R

Есть ли в фактор-кольце R/I нейтральный элемент? Если да, то как он выглядит?

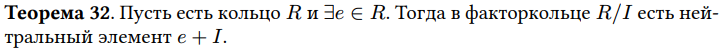
R - коммутативное кольцо.

Фактор-кольцо R\I коммутативно?

Да

Какие идеалы есть у поля P?

Только I=0 и I=P

Дайте определение

нильпотентный элемент

Дайте определение

Иденпотентный элемент

Что можно сказать про характеристику кольца с единицей и без делителей нуля.

Что можно сказать про характеристику поля?

Характеристикой конечного поля является простое число.

Дайте определение

Область целостности (целое кольцо)

Дайте определение

Евклидово кольцо

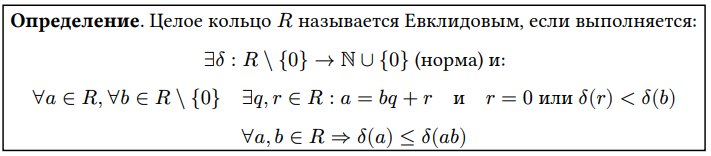
Приведите пример Евклидового кольца и нормы этого кольца.

Например, \mathbb{Z} - Евклидово. \delta (a) = |a|

Назовите свойства нормы.

R - Евклидово кольцо. Когда \delta (ab) = \delta (b)?

a, b \in R \backslash \{0\}, \quad \delta (ab) = \delta (b) \iff a \in R^*

Чему ровна норма единицы евклидового кольца?

Норме любого обратимого элемента.

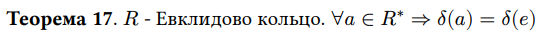
Чему равна норма обратимого элемента в евклидовом кольце?

Норме единицы

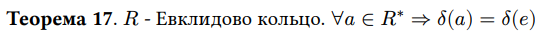
Дайте определение

Ассоциированные элементы

Если в Евклидовом кольце a, b \in R \backslash \{0\} и a|_b, b|_a, то элементы a,b … ?

Ассоциированные

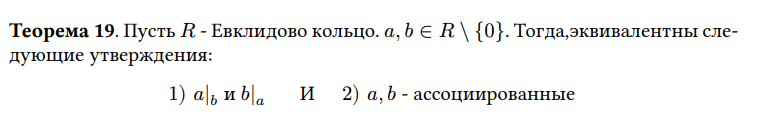
Дайте определение

НОД элементов в Евклидовом кольце

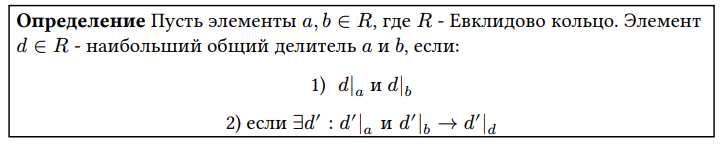
a,b \in R - Евклидово.
Если d = НОД(a, b) и c = НОД(a, b), то элементы d и c….?

Ассоциированные

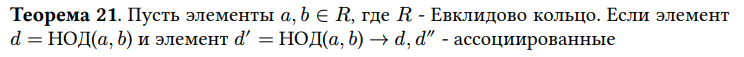
Приведите пример ассоциированных элементов

НОД(5,2)=1. В то же время НОД(5,2)=-1. Значит 1 и −1 ассоциированы

Алгоритм Евклида для нахождения НОД

Дайте определение

Взаимно простые элементы

Элементы в кольце R называются взаимно простыми, если их НОД = 1

Расширенный алгоритм Евклида

Дайте определение

Неразложимые элементы