phd

Štatistiku v súčasnosti možno definovať ako:

- Číselné údaje a ich funkcie o skúmaných hromadných javoch

- Praktickú činnosť, ktorá sa zaoberá získavaním číselných údajov o hromadných javoch

- Vednú disciplínu, ktorá sa zaoberá metódami skúmania hromadných javovčasti

Definícia pojmu štatistika

Štatistiku možno definovať ako vednú disciplínu, ktorá skúma zákonitostí hromadných javov, metódy

zberu, spracovania, interpretácie a analýzy údajov

Pod pojmom štatistika sa rozumejú dva disciplíny a to:

- Deskriptívna, teda opisná štatistika, ktorej cieľom je opísať skúmaný súbor pomocou grafov,

tabuliek a malým počtom charakteristík

- Inferenčná, teda induktívna štatistika, ktorej cieľom je na základne preskúmania výberového

súboru odhadnúť vlastností základného súboru, teda robiť závery o celku na základe preskúmania

jeho

Matematická štatistika

Matematická štatistika predstavuje oblasť štatistiky, ktorá na získanie výsledkov používa vyššie

matematické nástroje, najmä teóriu pravdepodobnosti s aplikáciou na náhodné premenné, jej súčasťou

je testovanie hypotéz

Veda

Vedu možno charakterizovať ako ucelený systém overených poznatkov o konkrétnej realite, ktoré sú

usporiadané do logického systému a boli získané pomocou vedeckých metód

Metodológia vedy

Metodológia vedy je disciplína, ktorej predmetom sú nástroje vedy.

Metodológia

Metodológia sa zaoberá systematizáciou, posudzovaním a navrhovaním stratégií a metód výskumu

Metóda

predstavuje konkrétny nástroj skúmania daného výskumného predmetu

Výskum

- možno charakterizovať ako systematické skúmanie prírodných a sociálnych javov s cieľom získať

poznatky popisujúce a vysvetľujúce svet okolo nás

- ide o širší pojem ako prieskum

- má presne stanovené pravidlá a postupy (prípravná etapa, etapa zberu dát, etapa spracovania dát

a etapa vyhodnocovania dát)

- charakteristiky:

• proces zhromažďovania údajov

• je systematický

• problematizuje a syntezuje doterajšie znalosti

• zahŕňa kritickú analýzu

• vedie k zvyšovaniu znalosti

Prieskum

činnosť, ktorá prináša nesystematizované a nekvantifikované

poznanie, väčšinou ide o jednu z etáp výskumu, ktorá sa vykonáva v terénne, obvykle bez širšieho

teoretického zázemia

Druhý výskumov

- Kvalitatívny – zameraný na objasnenie a vysvetlenie sociálnych javov z pohľadu jedincov či

skupín, výsledky a zistenia sa uvádzajú v slovnej (nečíselnej podobe). Používa predovšetkým

otvorené otázky a ide o výstižný a podrobný popis.

- Kvantitatívny – predstavuje testovanie teórií prostredníctvom preverovania vzťahu medzi

premennými. Premenné môžu byť merané pomocou konkrétnych nástrojov a následne

vyhodnocované využitím rôznych štatistických prístupov. Pracuje s číselnými údajmi. Zisťuje

množstvo, rozsah alebo frekvenciu výskytu javov resp. mieru (stupeň)

- Zmiešanmy

Základne komponenty kvantitativneho výskumu

• Výskumný problém = identifikácia výskumného cieľa, výskumného problému a výskumných

otázok

• -Teória = spracovanie teoretického rámca predpokladá prehľad o doterajšom výskume a teda

zodpovedá práci s informačnými zdrojmi. Slúži k formulovaniu výskumného problému vrátane

ujasnenia si oblasti tém výskumu.

• Hypotézy = obvykle sa formujú ako vecné tvrdenia, v ktorých sa vyskytujú premenné, s ktorými

sa vo vedeckom výskume bude pracovať. Následne dochádza k premene vecnej hypotézy na

štatistickú hypotézu, ktorú je možné overiť pomocou štatistických metód.

• Operacionalizácia = prevod definovaných pojmov na skúmateľné (merateľné) ukazovatele

(premenné)

• Výskumný súbor

• Realizácia merania či pozorovania = zber dát prostredníctvom vhodnej metódy

• Usporiadanie a kritické preverenie údajov = zistenie, či údaje nie sú skreslené alebo neúplné a ich následné kódovanie

• Testovanie hypotézy = zvyčajne s využitím štatistických metód

• Vyvodenie záverov výskumu = konečným cieľom vedeckej štúdie je interpretovať výsledky a vyvodiť závery, ale aj pripraviť návrhy či odporúčania

• Verifikácie = vzťahovanie výsledkov testovania k teórií, a to najmä ak sa hypotézy nepotvrdia

Etapy kvantitatívneho výskumu

1. Prípravná etapa

- Zadefinovanie cieľa výskumu a výskumného problému

- Získavanie informácií o skúmanej téme

- Súčasťou je operacionalizácia (identifikácia premenných skúmaného javu a formulovanie

hypotéz)

2. Etapa zberu dát

- Najdôležitejší krok práce výskumníka

- Metóda zberu údajov sa vyberá na základe kritickej analýzy výhod a nevýhod spojených s

niekoľkými alternatívami zberu údajov

- Dĺžka trvania môže byť rôzna

3. Etapa spracovania dát

- Dôležitá redukcia intervalových údajov a nastolenie poriadku do veľkého množstva údajov

- Zisťovanie odľahlých hodnôt sa odporúča ešte pred ostatnými krokmi etapy spracovania dát

- Odľahlé hodnoty je potrebné zo súboru vylúčiť

4. Etapa vyhodnocovania dát

- Spracované výsledky sa analyzujú a interpretujú v širšom kontexte vzhľadom k cieľu výskumu,

formulujú sa závery a odporúčania pre prax

- Je dôležité aby odporúčania vychádzali z realizovaného výskumu a boli potencionálne

realizovateľné

Výskumný problém

- predstavuje problém, ktorého sa otázka stáva predmetom výskumu

- je ho potrebné vymedziť vo všetkých výskumných projektov na akúkoľvek tému

Vúskumná otázka

- ide o formuláciu respektíve transformáciu výskumného problému do podoby otázky

- možno ju rozdeliť na 2 typy:

• všeobecné – široko zamerané, nie je možné na nich priamo odpovedať

• špecifické – detailnejšie a konkrétnejšie, pričom je možné na nich priamo odpovedať

- v záverečných prácach sa stretávame s dvoma typmi a to:

• zamerané na rozdiel

• zamerané na súvislosto

Premenná

- čokoľvek čo možno vo výskume merať alebo ovplyvniť

- symbolické vyjadrenie vlastnosti určitej skúmanej jednotky

- musí disponovať minimálne dvoma hodnotami (napr. premenná „rod“ môže

nadobúdať hodnotu muž alebo žena)

- klasifikácia:

o kvalitatívne, ktoré je možné ďalej deliť na: nominálne a ordinálne

o Kvantitatívne, ktoré je možné ďalej deliť: na intervalové a pomerové

Kvalitatívnu premennú

opisujeme slovne (napríklad: farba očí, školský prospech rodinný stav...).

Nominálne premenné

- Vyjadrujú skúmaný jav slovne

- Je im potrebné pri spracovaní dát priradiť číslo, ktoré nevyjadruje množstvo, mieru,

intenzitu alebo poradie

- Špecifickým príkladom nominálnej premennej je binárna premenná, ktorá sa označuje

aj ako dichotomická a môže nadobúdať iba dve hodnoty (muž/žena, áno/nie...)

Ordinálne premenné

- Vyjadrujú skúmaný jav v kategóriách, ktoré sú v určitom type hierarchického vzťahu (vyšší, spokojnejší, silnejší...)

- Nie je jasná veľkosť rozdielu

Kvantitatívne premenné

- Ich hodnoty sú reálne čísla, o dvoch hodnotách

- Možno povedať, či sú rovnaké alebo rôzne

- Možno ich usporiadať do poradia

- Možno určiť o koľko je jedna hodnota väčšia ako druhá a naopak

- Delenie:

1. hľadisko:

▪ diskrétne, ktoré nadobúdajú konečný alebo spočítateľný počet obmien

(počet detí, bodov...)

▪ spojité, ktoré majú ľubovoľnú číselnú hodnotu z istého intervalu alebo

zjednotenia intervalov (výška, hmotnosť, teplota, vek...)

2. hľadisko

▪ intervalové

• vyjadrujú veľkosť javu prostredníctvom číselných hodnôt, medzi

ktorými je jasná veľkosť rozdielu

• vieme určiť o koľko je jedna hodnota väčšia ako druhá, ale

nevieme určiť koľkokrát je jedna hodnota väčšia ako druhá

• nemá prirodzený nulový bod

▪ pomerové

• ide o špecifický druh intervalovej premennej

• majú presne definovaný bod absolútnej nuly, pod ktorú ich hodnota nikdy nemôže klesnúto

Hypotéza

- predstavuje predpokladanú odpoveď na otázku, ktorá vychádza z cieľa výskumu

- jej vlastnosťou je verifikovateľnosť, teda tvrdenie, ktoré prináša hypotéza musí byť

empiricky overiteľné

- pravidlá formovania

1. hypotéza je oznamovacia veta

2. hypotéza obsahuje dve premenné

3. premenné sa dajú presne zisťovať (merať, kategorizovať)

- každá hypotéza musí mať v sebe zahrnutý potencionálny rozdiel alebo vzťah medzi

dvoma premennými

- nemôže byť čiastočne potvrdená

- členenie:

• východiskové - vychádzajú z poznania a rozboru problému, ktorý chceme vo výskume riešiť

• pracovné - konkretizujúce východiskové hypotézy, ktoré majú podobu podmienene pravdivého výroku, no niekedy majú iba čiastkovú podobu

• štatistické - koncipiované, tak aby mohli byť pomocou empirických (nameraných,

zistených) dát potvrdené alebo vyvrátené; majú spravidla podobu nulovej hypotézy (H0), ktorú by výskumník rád zamietol, oproti nej kladieme alternatívnu hypotézu (H1)

Primárne dáta

predstavujú dáta, ktoré sú získavané alebo nové, napríklad prostredníctvom

experimentu, dotazníka, pozorovania alebo interview (zber môže trvať dlhší čas)

Sekundárne dáta

predstavujú dáta, ktoré už existujú pred samotným výskumom a vznikli

v rámci iného výskumu alebo procesu (možno ich získať z literárnych zdrojov, oficiálnych

a neoficiálnych správ, knižných či iných databáz...)

Meranie

musí byť validné, teda merať to čo má merať. Validitu možno charakterizovať ako

platnosť. Meranie musí byť spoľahlivé.

Odľahlé a extrémne hodnoty

- výrazne sa líšia od ostatných

- majú negatívny vplyv na výsledky štatistických testov

- zapríčinené porušením správneho postupu pri meraní alebo vyhodnocovaní dát/výsledkov merania (napríklad nesprávnym vyplnením dotazníka, ľudským faktorom, chybou pri zaznamenávaní)

- na zistenie existujú rôzne štatistické testy:

• Grubsov test

• Dixonov test

- niekedy kvôli jednoduchosti postačí aj grafická metóda, ako napr. boxplot

- odporúča sa ich zistiť ešte pred ostatnými krokmi etapy spracovania dát

- takéto hodnoty sa musia zvyčajne vylúčiť zo súbor

kódovanie dát

- používa sa v prípade kvantitatívneho výskumu, pri ktorom sa každému variantu

„odpovede“ priradí určitý symbol najčastejšie ide číslo

- predstavuje proces sumarizovania a opätovného prezentovania údajov s cieľom

poskytnúť systematický popis zaznamenaného alebo pozorovaného javu

- v etape spracovania dát musí výskumník upraviť dáta do takej podoby, aby s nimi

mohol pracovať

- prostredníctvom kódovania je možné niekoľko odpovedí zredukovať na malý počet

tried, ktoré obsahujú kritické informácie požadované analýzou

- zakódované údaje môže výskumník editovať v štatistickom programe – voliť

štatistické operácie nevyhnutné k dosiahnutiu stanovených cieľov

Triedenie dát

- usporiadanie štatistického súboru do skupín podľa štatistického znaku (znakov)

- zásady:

o úplnosť – každá štatistická jednotka musí byť zatriedená

o jednoznačnosť – každú štatistickú jednotku musíme zatriediť práve do jednej

skupiny

- podľa počtu znakov možno deliť triedenie na

• jednostupňové/prvostupňové

  • podľa 1 triediaceho znaku

  • zisťuje sa početnosť, ktorá sa uvádza v absolútnych alebo relatívnych početnostiach

  • odporúča sa použiť aj deskriptívne charakteristiky

    • miery polohy

    • miery variability

    • miery tvaru

• viacstupňové triedenie

  • so súčasným použitím viacerých triediacich znakov

  • možno použiť kontingenčné tabuľky

Štatistické spracovanie

možno definovať ako usporiadanie a zhrnutie informácií, ktoré sa najskôr robí pomocou tabuliek a grafov (obrázkov), ktorých výhoda spočíva v úspornosti a v tom, že vyjadria viac než dlhé slovné pasáže.

Tabuľka

- obvyklý nástroj pre súhrnnú a prehľadnú prezentáciu údajov či výsledkov

- užitočné sú tabuľky, ktoré rýchlo a prehľadne informujú o základných parametroch, či podstate výstupu

- najznámejšie formy:

• tabuľky početností

  • predstavujú podrobný rozpis zastúpení kategórií alebo hodnôt danej premennej v súbore dát

  • obvykle obsahujú:

    • relatívne početnosti (%)

    • absolútne početnosti (koľkokrát)

    • kumulatívne početností (spolu)

• kontingenčné tabuľky, ktoré predstavujú dvojrozmerné rozdelenie početnost

Graf

- Je potrebné aby mal jasne určený názov a účel, čo znamenajú jednotlivé osi, triedy,

stĺpce, zdroj, škály každej osi s vyznačením začiatku

- Najčastejšie používané typy:

• Bodový graf

• Stĺpcový graf

• Histogram

• Spojnicový graf

• Krabicový graf

Dotazníková metóda

- Jedna z najčastejšie využívaných metód vedeckého výskumu

- Vhodná na zisťovanie jednoduchých nekomplikovaných javov, ako sú názory, postoje,

predstavy, potreby, správanie respondentov, miery, frekvencie...

- Za krátky čas a nízke náklady sa dá získať relatívne veľké množstvo dát

Dotazník

- Spôsob písomného kladenia otázok a získavania písomných odpovedí

- Formulár, v ktorom sú vopred naformulované otázky, na ktoré respondent odpovedá

- Otázky sa môžu týkať znalostí, názorov, postojov, preferencií, motivácie, osobných

a demografických charakteristík

- V niektorých literárnych zdrojov sa namiesto otázok uvádzajú položky

Štandardizovaný dotazník

- Má známu validitu a spoľahlivosť, ktorá bola overená už v predošlých výskumoch

- Umožňuje porovnávať výsledky rôznych autoroch

- V prípade, že výskumník nemá dostatočné skúsenosti s metodológiou, je vhodnejšie

použiť existujúce štandardizované dotazníky, ale treba uviesť zdroj, z ktorého boli

prebraté

Neštandardizovaný dotazník

možno charakterizovať ako dotazník vlastnej konštrukcie, ktorý sa aplikuje v rámci jedného výskumu.

Štruktúra dotazníka

- Oslovenie respondenta

- Inštruktáž, ako dotazník vyplňovať

- Samotné otázky (položky)

- Poďakovanie

Pilotná štruktúra

Prostredníctvom pilotnej štruktúry sa overuje, či sú otázky v dotazníku zrozumiteľné

a jednoznačné.

Predvýskum

Predvýskum možno charakterizovať ako komplexnú previerku výskumných metód, nástrojov, stratégie, niekedy i hypotéz a možnosti spracovania

Zásady tvorby otázok v dotazníku

-       Jednoznačnosť otázok – otázku musia pochopiť všetci respondenti rovnako  

-       Stručnosť otázok – nesmie sa stať, že respondent na konci zabudne, čo bolo na začiatku  

-       Zrozumiteľnosť otázok – používanie slov, ktoré respondenti poznajú, nemali by sa objavovať cudzie slová, skratky, nárečové slová a slang

-       Používanie eufenizmov  

-       Používanie projektívnych otázok

-       Nepoužívanie sugestívnych otázok  

-       Nepoužívanie širokého znenia otázok  

-       Vyhýbanie sa dvojitým otázkam  

-       Vyhýbanie sa záporným výrazom  

-       Používanie naozaj nevyhnutných otázok  

-       Používanie otázok, ktoré merajú to, čo chceme merať  

-       Používanie otázok, ktoré majú úplné varianty odpovedí – ak si výskumník nie je istý, či uviedol všetky možné varianty, použije polootvorené otázky  

Druhy otázok

-       Otvorené – neponúkajú žiaden variant odpovede, preto na nich musí respondent odpovedať sám  

-       Zatvorené  o  majú vopred formulované varianty odpovedí o  ich výhoda spočíva v jednoduchom spracovaní  o  podľa počtu ponúkaných odpovedí sa delia na:  

• Dichotomické (dva varianty)

• Polytomické (niekoľko variant)

  •   Výberové (1 možnosť)

  • Výpočtové (viac možností)

  •   Stupnicové (poradie)

-       Polootvorené otázky – okrem variantov možných odpovedí ponúkajú respondentovi aj možnosť odpovedať vlastnými slovami  

-       Demografické otázky  o špecifikujú respondenta na základe veku, rodu, bydliska, vzdelania, rodinného stavu a zamestnania, nemali by sa číslovať

-       Kontrolné otázky  o umožňujú zvýšiť validitu, pretože sa prostredníctvom nich pýtame znova na niečo, čo sme už v predchádzajúcich otázkach od respondenta mohli dostať odpoveď

Tvorba škál

- pri tvorbe škál si musí výskumník uvedomiť, že aký je výskumný problém, cieľ výskumu a aké matematicko-štatistické operácie chce v rámci napĺňania cieľa realizovať

- škála zodpovedá jednotlivým hodnotám, ktoré premenná môže nadobúdať

- posudzovacie (ratingové) škály sú formou možností odpovede na uzatvorené otázky

Klasifikácia škál

• Numerické – vyjadrené číslami

Rozhodne súhlasím 1 – 2 – 3 – 4 – 5 Rozhodne nesúhlasím

• Verbálne – môžu byť obmedzené (max 5-6 stupňov)

Rozhodne súhlasím – Súhlasím – Skôr súhlasím – Skôr nesúhlasím – Nesúhlasím – Rozhodne nesúhlasím

• Grafické – spestrenie dotazníka (zoznam emotikonov)

• Unipolárne

  • majúce jeden pól

  • umožňujú posudzovať rôzny stupeň jednej vlastnosti

Nepodnetné – Málo podnetné – Podnetné – Veľmi podnetné

• Likertové

  • merajú postoje a názory ľudí

  • výrok + stupnica

  • štandardná má 5 polôh

Úplne súhlasím – Súhlasím – Nemám vyhradený názor – Nesúhlasím – Vôbec nesúhlasím

- ďalšie delenie škál je podobné, ako sa uvádza pri druhoch premenných:

• nominálne (slovne vymenovávajú a zachytávajú výskyt daného skúmaného javu)

• ordinálne/poradové (používa sa v prípade , ak chce výskumník pracovať s poradím)

• intervalové a pomerové (jednotlivé položky sú vyjadrené, tak aby boli medzi nimi jasné veľkosti rozdielov (príjem v €, vek...)

Štatistický súbor

možno definovať ako konečnú neprázdnu množinu objektov, ktoré sú predmetom štatistického skúmania

Rozsah súboru

• predstavuje počet prvkov štatistického súboru

• prvky štatistického súboru sú štatistické jednotky

Základný súbor

- možno označiť ako populáciu

- ide o všetky jednotky, ktoré sa týkajú výskumného problému

- nie vždy je možné získať informácie o všetkých jednotkách základného súboru z personálnych, finančných ako aj materiálnych a časových dôvodoch

Výberový súbor

- možno označiť, ako výskumný súbor alebo výskumnú vzorku

- tvoria ho jednotky, ktoré sa stávajú súčasťou výskumu

- kľúčová požiadavka spočíva, v tom aby verne zobrazoval podobu základného súboru,

a teda, aby bolo možné výsledky výskumu zovšeobecniť na celú populáciu

- nazýva sa aj ako reprezentatívny súbor

- na vyvodenie záverov o populácií sa používa induktívna štatistika

Výskumný súbor

- označuje sa aj ako výskumný vzorka alebo podmnožina populácie

- získať údaje o celej populácií je zvyčajne nepraktické alebo dokonca nemožné

z hľadiska času alebo peňazí, musíme sa často spoliehať iba na informácie získané zo

vzorky

- vytvárame ho na základe určitých pravidiel

- výberu musí byť venovaná náležitá pozornosť:

• prvým krokom je jasné definovanie populácie

• ak je prvý krok splnený, môže sa použiť jedna zo stratégií výberu

Náhodne pravdepodobnostné výbery

• všetky jednotky základného súboru majú rovnakú pravdepodobnosť, že sa do výskumnej vzorky dostanú

• objekty sú vyberané z populácie na základe teórie pravdepodobnosti

• druhy:

  • jednoduchý náhodný výber – výskumník musí mať, k dispozícií zoznam všetkých jednotiek základného súboru a jednotky, ktoré budú tvoriť

    • náhodný výber sa môžu vybrať buď losovaním alebo prostredníctvom generátora náhodných čísel

  • viacstupňový – dopĺňa jednoduchý, v prvom kroku urobíme náhodný výber vysokých škôl a fakúlt, druhom sa na vybraných fakultách vyberú náhodne študijné skupiny

  • stratifikovaný – spočíva v rozdelení základného súboru na homogénne skupiny podľa určitého kritéria a z týchto skupín sa potom respondenti vyberajú náhodným výberom

  • systematický – prvky sú náhodne zoradené vzhľadom ku skúmanému znak napr. podľa abecedy a náhodne sa vyberie jeden prvok napr. 10, 20, 30, 40,.... respondent

Nenáhodné výbery

• každá jednotka populácie nemá rovnakú šancu byť súčasťou vzorky

• odvodený od subjektívneho úsudku – výsledky môžu byť skreslené

• druhy:

  • Metóda snehovej gule – výskumník najprv idenfikuje niekoľko vhodných osôb, ktoré patria do cieľovej populácie -> tieto osoby sú požiadané, aby odporučili ďalších ľudí, ktorí tiež spĺňajú kritéria výskumu -> noví respondenti opäť odporučia ďalších a teda „výber narastá ako snehová guľa“

  • Zámerný výber – jednotlivé prvky sa vyberajú subjektívne na základe osoby realizujúcej štatistické šetrenie

  • Konvenčný – prvky sú vyberané v atakom poradí, v akom boli zaznamenané (napr. prvých 10 zákazníkov, ktorí vstúpili do obchodu)

  • Kvótny – dopredu máme stanovený určitý počet jedincov v rôznych kategóriách, napríklad určitý počet obyvateľov z kategórií ako vek, pohlavie, vzdelanie, ekonomický status a pod.

  • Dostupný – beriem to čo mám, používa sa pri jednoduchej dostupnosti respondentov

Veľkosť výskumného súboru

počet subjektov (napr. respondentov), ktorých zahŕňame do výskumu

Rozhodovanie o veľkosti súboru môže ovplyvniť:

- Výskumný problém – ak je naším záujmom zistiť predvolené preferencie,neuspokojíme sa s údajmi získaných do 100 respondentov

- Veľkosť populácie – čím väčšia je populácia, tým viac respondentov by sme mali mať vo výskumnom súbore

- Spôsob zberu údajov – ak použijeme dotazníkovú metódu, výskumný súbor by mal

byť rozsiahlejší ako napr. pri pozorovaní

- Členitosť skúmaných premenných – ak má premenná veľa hodnôt, súbor sa rozloží na

veľa častí, ktoré môžu mať nízke početnosti

- Použité stupne triedenia – čím viac stupňov triedenia sa pri spracovaní dát použije tým

väčšia by mala byť veľkosť výberového súboru

- Miera pravdepodobnosti štatistických výpovedí – pri realizovaní štatistických testov je

potrebné zistiť, či získané dáta spĺňajú kritéria parametrických alebo neparametrických testov

- Možnosti štatistického spracovania údajov – použitie niektorých štatistických metód si vyžaduje väčšie výskumné súbor

Štatistické miery polohy

• patria do deskriptívnej štatistiky

• deskriptívna (popisná) štatistika predstavuje číselné hodnoty, ktoré charakterizujú celý súbor

• predstavujú typickú hodnotu znaku v danom súbore

• v prípade kvantitatívnej premennej charakterizujú súbor z hľadiska polohy hodnôt premennej na súradnicovej osi

• Aritmetický priemer

• Medián

• Módus

• Kvantity

• Kvartily

• Decily

Aritmetický priemer

• predstavuje súčet všetkých hodnôt znaku delený ich počtom

• môžu ho výrazne ovplyvniť extrémne hodnoty

• hoci v praxi je najviac využívaný práve aritmetický priemer poznáme ešte:

  • vážený aritmetický, geometrický a harmonický priemer

Medián

• predstavuje strednú/centrálnu hodnotu súboru

• ak dáta usporiadame podľa veľkostí vzostupne platí, že 50% nameraných dát je menších alebo rovných mediánu

• neovplyvňujú ho extrémne hodnoty

Módus

• predstavuje najpočetnejšiu hodnotu v súbore

• určený len pre jednovrcholové rozdelenie

• 1 módus v súbore – jednovrcholové rozdelenie

• viac módusov – viacvrcholové rozdelenie

Kvantily

• predstavujú charakteristiky rozdeľujúce vzostupne usporiadaný súbor na q rovnako početných častí

• najčastejšie používané: medián, kvartily, decily, percentily a promile

  • q=2 – 1 kvantil – medián

  • q=4 – 3 kvantily – kvartily

  • q=10 – 9 kvantilov – decily

  • q=100 – 99 kvantilov – percentily

  • q=1000 – 999 kvantilov – promile

Kvartily

• predstavujú hodnoty, ktoré delia vzostupne usporiadaný súbor na 4 časti

• Dolný kvartil (Q1) – oddeľuje 25% (1/4) najnižších hodnôt od 75% (3/4) najvyšších hodnôt premennej

• Stredný kvartil (Q2) – medián

• Horný kvartil (Q3) – oddeľuje 75% (3/4) najnižších hodnôt od 25% (1/4) najvyšších hodnôt premenne

Decily

predstavujú hodnoty, ktoré delia vzostupne usporiadaný súbor na 10 rovnako početných častí

Percentily

predstavujú hodnoty, ktoré delia vzostupne usporiadaný súbor na 100 rovnako početných častí a promile na 1000 rovnako početných častí

Štatistické ukazovatele miery variability

• predstavujú číselné hodnoty, ktoré charakterizujú premenlivosť (variabilitu) hodnôt štatistického znaku v súbore

• čím je premenlivosť hodnôt znaku väčšia, tým je aj väčšia charakteristika variability

• patria do deskriptívnej štatistiky

• Variačné rozpätie

• Medzikvartilové rozpätie

• Rozptyl

• Smerodajná odchýlka

• Variačný koeficient

Variačné rozpätie

• rozdiel medzi najväčšou a najmenšou hodnotou skúmanej premennej

• výhoda: ľahký výpočet

• nevýhoda: ovplyvnenie extrémnymi hodnotami

Medzikvartálove rozpätie

• rozdiel medzi prvým a tretím kvartilom (75% a 25%), čo reprezentuje oblasť 50 % hodnôt premennej

• je ho možné grafický znázorniť pomocou tzv. krabicového grafu

Rozptyl

• miera variability, ktorá meria premenlivosť znaku v zmysle odlišnosti jednotlivých hodnôt štatistického znaku od ich aritmetického priemeru

• čím je väčší, tým viac sa údaje odchyľujú od priemeru

Smerodajná odchýlka

• odmocnina rozptylu

• vyjadruje variabilitu v pôvodných merných jednotkách

• ak je jej hodnota vysoká, tak sa všetky čísla v súbore značne líšia

• ak je jej hodnota nízka, tak sa všetky čísla v súbore sú si podobné

Variačný koeficient

• relatívna charakteristika variability

• používa sa pri porovnávaní variability dvoch štatistických súboroch

• nevhodný: hodnoty skúmanej premennej nadobúdajú hodnoty s rôznym znamienkom

• priemerná hodnota = 0 – nie je definovaný

Štatistické ukazovatele miery tvaru

• dva štatistické súbory, ktoré majú rovnaké miery polohy a variability, ešte nemusia byť

zhodné, môžu sa odlišovať tzv. mierami tvaru, medzi ktoré patrí šikmosť a špicatosť

• Šikmosť

  • meria smer a stupeň a asymetrie rozdelenia premennej

  • miera, akou sa súbor, resp. jeho rozdelenie odlišuje od normálneho rozdelenia

  • pri symetrickom rozdelení sú aritmetický priemer, medián a modus rovnaké

  • koeficient šikmosti kladný = pravostranná šikmosť

  • koeficient šikmosti záporný = ľavostranná šikmosť

  • koeficient rovný 0 = symetrické rozdelenie

• Špicatosť

  • meria koncentráciu hodnôt štatistického znaku okolo ich strednej hodnoty

  • ukazovateľom je koeficient špicatosti

  • špicatý tvar rozdelenia = vyšší stupeň koncentrácie prostredných hodnôt = koeficient je kladný

  • ploché rozdelenie početností = koeficient je záporný

  • kladná špicatosť = koeficient je rovný 0

Štatistická hypotéza

• predstavuje tvrdenie o vlastnostiach základného súboru, prípadne viacerých základných súboroch, pričom nevieme, či je pravdivé alebo nie

• vzťahuje sa buď k tvaru, alebo k parametrom rozdelenia pravdepodobnosti a môžeme ju overiť testovaním

• je ju možné odvodiť pomocou štatistických metód na základe údajov výberového súboru

• H0 – hypotéza, ktorej platnosť overujeme, označuje sa ako nulová hypotéza, pri testovaní sa ďalej uvádza, čo bude platiť ak nebude platná

• H1 – alternatívna hypotéza/druhé tvrdenie

Testovanie štatistických hypotéz

• predstavuje postup, ktorým overujeme platnosť štatistických hypotéz

• cieľom je zistiť, či je vhodné zamietnuť H0 v prospech H1

• rozhodnutie o tom či H0 zamietame, alebo ju nevieme zamietnuť sa realizuje tak, že sa urobí štatistický test, pomocou, ktorého sa vypočíta testovacia štatistika, určí sa kritická hodnota a kritický obor a následne sa zistí, či testovacia štatistika do kritického oboru patrí, alebo nie

P-hodnota

- predstavuje najnižšiu pravdepodobnosť pre zamietnutie H0 a je určená na základe testovacieho kritéria

- nadobúda hodnoty od 0 do 1

- správny výpočet poskytne štatistický program

Hladina významnosti

- kritická hodnota pre P-hodnotu

- označuje sa ako alfa

- rozhodovacie pravidlo:

• P-hodnota ≤ a = H0 zamietame

• P-hodnota > a = H0 nevieme zamietnuť

• Nevieme zamietnuť nerovná sa prijať!

Chyby, ktorý sa môžeme dopustiť, môžu byť dvojaké

• Chyba I. druhu – nulovú hypotézu zamietame, avšak v skutočnosti platí, jej pravdepodobnosť sa nazýva hladina významnosti a, riziko chyby I. druhu sa znižuje nízkou hladinou významnosti

• Chyba II. druhu – nulovú hypotézu nevieme zamietnuť (nezamietame), avšak neplatí. Pravdepodobnosť tejto chyby označujeme ako β.

Pri písaní záverečných prací sa najčastejšie stretávame s hypotézami zameranými na:

- Existenciu štatisticky významného rozdielu

- Existenciu štatisticky významnej súvislosti (vzťahu, závislosti)

- Existenciu určitého rozdelenia pravdepodobnosti

Normálne rozdelenie

sa inak nazýva aj Gaussovo rozdelenie pravdepodobnosti, patrí medzi najdôležitejšie a v štatistickej praxi najčastejšie používané pravdepodobnostné rozdelenie

Na overenie normality existuje mnoho testov

• Jarque-Berra test, ktorý je vhodný pre rozsah výberu viac jednotiek v súbore ako 100.

• Shapiro-Wilkov test, ktorý je vhodný pre výbery rozsahu 7 ≤ n < 30 (n je väčšie alebo rovné 7 a zároveň menej ako 30)

• Doornik-Hanseno test – vhodný pre rozsah výberu n >50 (viac ako 50 jednotiek)

• Kolmogorovov-Smirnovov test – vhodný pre rozsah výberu n ≤ 30 (n je väčšie alebo rovné 30)

• Lilieforsov test – vhodný pre malý aj veľký rozsah súboru - UNIVERZÁLNY

Parametrické testy vs. Neparametrické testy

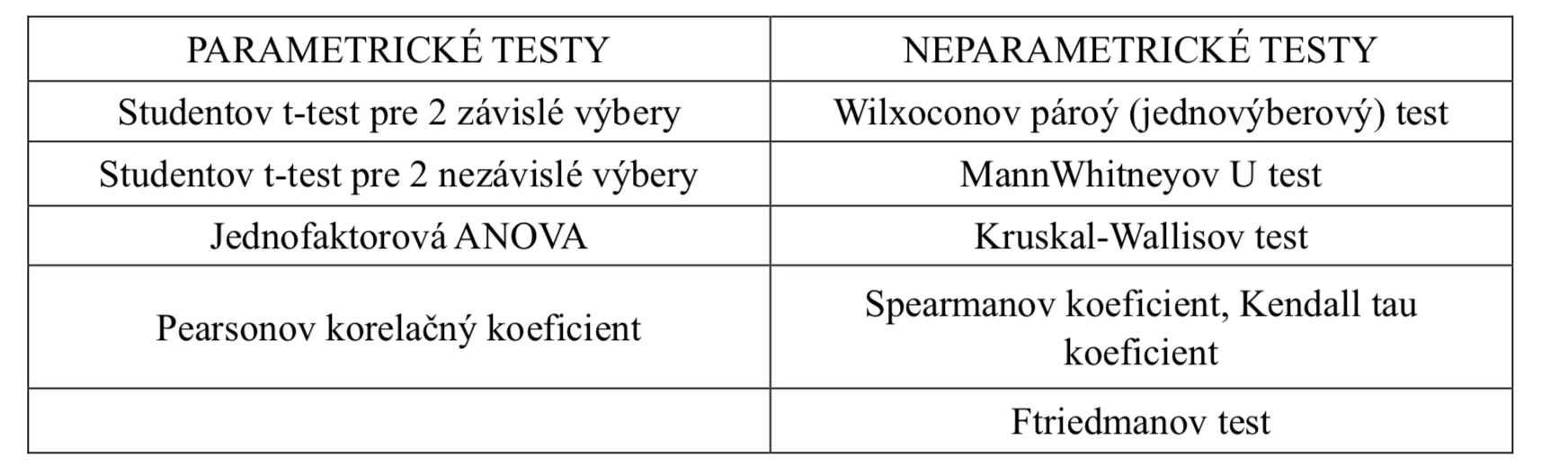
Studentov t-test pre dva závislé výbery (rozdiel)

testuje, či existujú rozdiely medzi dvoma závislými výbermi

Studentov t-test pre dva nezávislé výbery (rozdiel)

testuje, či existujú rozdiely medzi dvoma nezávislými výbermi

Jednofaktorová ANOVA (rozdiel)

- predstavuje najjednoduchšiu formu analýzy rozptylu

- testuje, či existujú rozdiely medzi troma alebo viacerými skupinami v jednej závislej

Wilconsov párový test (rozdiel)

testuje, či existujú rozdiely medzi dvoma závislými výbermi

Mann-Whitneyov U-test (rozdiel)

testuje, či existujú rozdiely medzi dvoma skupinami v jednej premennej

Kruskal-Wallisov test (rozdiel)

testuje, či existujú rozdiely medzi troma alebo viacerými skupinami v jednej závislej premennej

Friedmanov test (rozdiel)

testuje, či existujú rozdiely medzi viacerými závislými výbermi

Postup pri testovaní štatistických hypotéz:

1. Stanovenie výskumnej hypotézy (po stanovení by sme už mali vedieť, ktoré potencionálne štatistické testy použijeme)

2. Stanovíme hladinu významnosti (najčastejšie a=0,05)

3. Otestujeme, či majú normálne rozdelenie (nominálne premenné sa netestujú)

4. Vyberieme správny štatistický test na overenie hypotézy (po testovaní normality sa rozhodne, či použijeme parametrický alebo neparametrický)

5. Stanovíme štatistické hypotézy

6. V štatistickom programe vykonáme príslušný štatistický test

7. Interpretujeme výsledky testu

• Ak je P-hodnota ≤ a = H1 sme potvrdili

• Ak je P-hodnota > a = H1 sme zamietli

KORELAČNÁ ANALÝZA

sa zaoberá meraním sily asociácie (závislosti, súvislosti) medzi premennými

Rozdiel medzi súvislosťou a závislosťou

V niektorých publikáciách sa rozlišuje pojem súvislosť (asociácia, vzťah, súvzťažnosť) a závislosť (pri ktorej zmeny nezávislej premennej vyvolávajú zmeny závislej premennej), no vo väčšine prípadov sa tieto pojmy nerozlišujú, ale naopak stotožňujú.

Kauzálna závislosť - zmena nezávislej premennej, ktorá vyvoláva zmeny v závislej premennej.

Intenzita (sila) korelácie

sa meria použitím korelačných koeficientov

Podľa druhu premenných, ktorých závislosť chceme zistiť, možno rozlíšiť pojmy

• korelácia = závislosť kvantitatívnych premenných

• poradová korelácia = závislosť ordinálnych premenných

• kontingencia = závislosť kvalitatívnych premenných

Pozitívna korelácia

predstavuje situáciu, pri ktorej ak pozorujeme vyššie hodnoty jednej premennej, taktiež pozorujeme vyššie hodnoty druhej premennej, platí to aj pri nižších hodnotách.

Negatívna korelácia

predstavuje situáciu, pri ktorej ak pozorujeme vyššie hodnoty jednej premennej, tak pozorujeme nižšie hodnoty druhej remennej, respektíve ak pozorujeme nižšie hodnoty jednej premennej, tak pozorujeme vyššie hodnoty druhej premennej

Pearsonov korelačný koeficient

• skúma mieru lineárnej závislosti

• používa sa pri kvantitatívnych veličinách, ktoré majú aspoň približné normálne rozdelenie

• vlastnosti:

  • nadobúda hodnoty z intervalu <-1;1>

  • pozitívna korelácia = úmerný vzťah

  • negatívna korelácia = neúmerný vzťah

  • je symetrický

  • dobre meria len priamkové vzťahy

  • 1 = dokonalá priama korelácia

  • -1 = dokonalá nepriama korelácia

  • závislý na odľahlých a extrémnych hodnotách

• Spearmanov koeficient poradovej korelácie

• používa sa na skúmanie korelácie dvoch ordinálnych (poradových) premenných, no možno ho použiť aj v prípade kvantitatívnych (intervalových a pomerových) premenných

• vlastnosti:

  • nadobúda hodnoty z intervalu <-1;1>

  • hodnoty blízke 0 = nezávislosť

  • hodnoty blízke 1 = závislosť (priamy monotónny vzťah)

  • hodnoty blízke -1 = závislosť (nepriamy monotónny vzťah)

Kendallov koeficient poradovej korelácie

• skúma mieru závislosti dvoch premenných, ktorá je založená na meraní závislosti medzi poradiami

• základný súbor sa označuje ako T

• výberový súbor sa označuje ako t

• vlastnosti:

  • nadobúda hodnoty z intervalu <-1;1>

  • ak sú náhodné premenné nezávislé t = 0

  • ak je hodnota t > 0, hovoríme o kladnom vzájomnom vzťahu

  • ak je hodnota t < 0, hovoríme o zápornom vzájomnom vzťah

Kontingencia a x2 test nezávislosti

• Pearsonov x2 test nezávislosti

  • overuje nezávislosti medzi dvoma kvalitatívnymi premennými

  • nesmie mať očakávanú početnosť menšiu ako 5 v žiadnej zo skúmaných buniek/skupín

  • celkový počet respondentov by nemal byť menší ako 40

• Cramerov koeficient V

  • skúma vzťahy medzi viacúrovňovými nominálnymi premennými

  • keďže ide iba o nominálne premenné, môžeme hovoriť len o sile vzťahu, nie o smere

• Koeficient Phi

  • skúma vzťah dvoch dichotomických nominálnych premenných

• Koeficient kontingencie C

  • skúma mieru závislosti medzi dvoma kvalitatívnymi znakmi

REGRESNÁ ANALÝZA

Cieľom regresnej analýzy je odhadnúť vzťah medzi závislou premennou, ktorá je spravidla označená ako Y a jednou alebo viacerými nezávislými premennými, ktoré sú označené ako X.

Úlohou regresnej analýzy je na základe nameraných hodnôt (x1,y1), (x2,y2)... (xn,yn) odhadnúť neznáme parametre β0 a β1 daného modelu, ktoré budeme označovať ako b0 a b1.

Regresný model má praktické využitie pri predikcií hodnoty závislej premennej pomocou hodnôt nezávislej premennej (nezávislých premenných).

Podľa počtu nezávislých premenných (x) rozlišujeme:

• jednoduchú regresnú analýzu, kedy uvažujeme iba jednu nezávislú premennú

• viacnásobnú (mnohonásobnú) regresnú analýzu, kedy uvažujeme viac ako jednu nezávislú premennú

Jednoduchá regresná analýza

• uvažujeme len jednu premennú

• majme výberový súbor s rozsahom n, pričom na každom jeho prvku meriame dva kvantitatívne znaky X a Y

• úlohou je na základe nameraných hodnôt (x1,x2), (y1,y2),...., (xn, yn) odhadnúť neznáme parametre β0, β1 daného modelu, ktoré budeme označovať ako b0 a b1

• metóda najmenších štvorcov umožňuje vypočítať parametre regresnej priamky b1 a b2, pričom základom výpočtu je predpoklad, že súčet štvorcov (druhých odmocnín) vzdialenosti jednotlivých bodov od tejto priamky je najmenší možný

• cieľom je zvoliť regresnú priamku, tak aby rozdiely medzi nameranými hodnotami y, a odhadnutými hodnotami y, boli minimálne

• b0 vypočítané = hodnota závislej premennej y, ak hodnota nezávislej premennej x je 0 = lokačná konštanta

• b1 meria priemernú zmenu premennej y vyvolanú jednotkovou zmenou nezávislej premennej x

• kladná hodnota b1 = pozitívna závislosť

• záporná hodnota b1 = negatívna závislosť

Viacnásobný lineárny regresný model

• použijeme ho v prípade, ak uvažujeme o viac ako jednej nezávislej premennej

• konštanta β0 = hodnota závislej premennej y, ak hodnoty všetkých nezávislých premenných sú nulové

• regresné koeficienty β1, β2,..., βk = merajú očakávanú zmenu premennej y vyvolanú jednotkovou zmenou príslušnej nezávislej premennej, za predpokladu nemennosti ostatných nezávislých premenných

Rezíduum (εi)

je náhodná chyba v lineárnom modeli, ktorá zahŕňa pôsobenie náhodných vplyvov alebo náhodných veličín, ktoré nie sú zahrnuté do modelu.

Závislá vs. nezávislá premenná

Závislak premenná sa označuje ako vysvetľovaná (y), skúma sa jej závislosť od iných premenných.

Nezávislá premenná sa označuje ako vysvetľujúca (x).

Konštanta

β0 je konštanta, ktorú interpertujeme ako hodnotu závislej premennej y. ak hodnota nezávislej premennej y je nulová, ide o tzv. lokačnú konštant

Regresný koeficient

β1 je regresný koeficient = meria priemernú zmenu premennej y vyvolanú jednotkovou zmenou nezávislej premennej x (kladná hodnota = pozitívna závislosť a regresná priamka rastie; záporná hodnota = negatívna závislosť a regresná priamka klesá)

Multikolinearita

• porušenie predpokladu o nezávislosti nezávislých premenných

• dôležitým predpokladom regresného modelu je vzájomná nezávislosť nezávislých premenných

• navzájom korelované premenné by nemali do modelu vstupovať súčasne

• k dokonalej multikolinearita dochádza, ak je medzi vysvetľujúcimi premennými exaktný lineárny vzťah

• pri nedokonalej (neúplnej) multikolinearite nemusia byť vysvetľujúce premenné exaktne lineárne závislé, ale stačí, že sú vysoko korelované