Systems Biology Final

BIOL 415 Final Exam

Emergent property

property of a system that cannot be assigned to features of a single component, but only becomes possible from nonlinear interactions between the system components

Compared to cell/molecular biology, systems biology is focused on…

• wet experiments

• models and simulation

• many elements that interact, feedback interaction

• few elements at a time, only forward interactions

• large and small models, mathematical & computational verification

• small models, intuitive verification

models and simulation; many elements that interact, feedback interaction; large and small models, mathematical & computational verification

Order the steps of the modeling process:

a. model use and applications

b. model design

c. goals, inputs, initial exploration

d. model analysis and diagnosis

e. model selection

c, e, b, d, a

A correlative model shows…

given x, the model predicts y (but doesn’t explain why)

An explanatory model shows…

that X correlates with Y, and also shows why X correlates with Z

Which type of model changes over time?

dynamic model

Which type of model does not change over time?

static model

Which type of model always produces the same output with the same input and parameters?

deterministic model

Which type of model produces the different outputs with the same input and parameters?

stochastic model

A _____ model has random variables, so the results of the model are probabilistic.

stochastic

Variable

represents a biological entity of interest in the model (gene, an individual, a collection of entities)

Parameter

a numerical characteristic of the system (pH, temp, reaction rate)

Interaction

the influence of one variable into another (regulation, production, degradation)

Parameter estimation utilizes both _____ and _____ to create numerical parameter values for the simulation.

data from experimental methods, optimization algorithms to fit the model to data

Steady state

a state where none of the variables change anymore

Sensitivity

how changing parameters changes model behavior

After creating a model, you can use it for…

applying the model as is; targeted manipulation and optimization toward a specific goal

Randomized network

a network containing nodes with random links that are connected with equal probability

Biological network

a network containing nodes not connected with equal probability; has hubs

Connection sparsity

only a very small portion of all possible edges are formed in a biological network; the probability that two nodes are connected are small

Randomized networks follow a _____ distribution of connections

Poisson

Biological networks follow a _____ distribution of connections.

power law

Hub

a node with a high number of connections

Small world behavior

each node in a network can be reached from any other node through a short path

_____ (Randomized/Biological) networks are also called scale free networks and exhibit small world behavior.

biological

Network motif

a recurring structural feature of a network/system that is found more than one would expect in a corresponding, randomly composed system

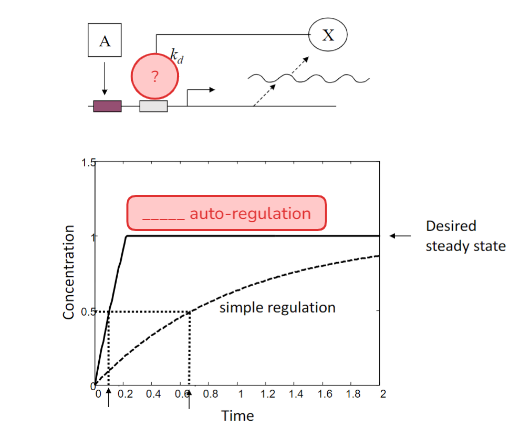
Which type of auto-regulation is shown here?

negative auto-regulation

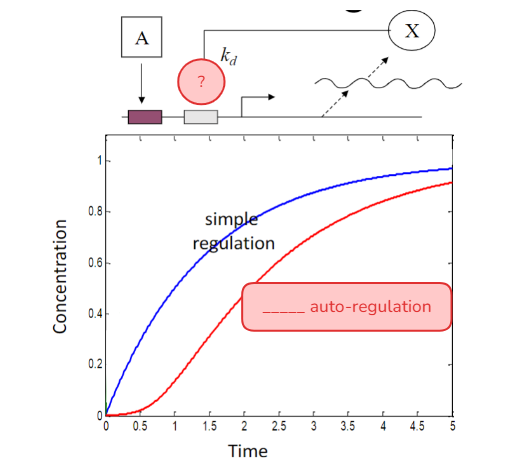
What type of auto-regulation is shown here?

positive auto-regulation

_____ (positive/negative) auto-regulation can use a strong promoter to give an initial fast production and then use autoregulation to stop the production at the desired steady state.

negative

_____ (positive/negative) auto-regulation can use a weaker promoter to give a slower initial production and then use autoregulation to stop the production at the desired steady state.

positive

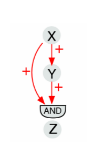
This image shows a ____ feed-forward loop.

coherent

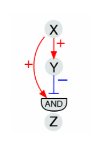
This image shows a _____ feed-forward loop.

incoherent

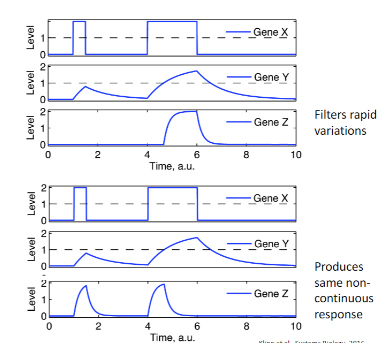
What type of network motif is shown by the top group of data?

coherent feed-forward loop

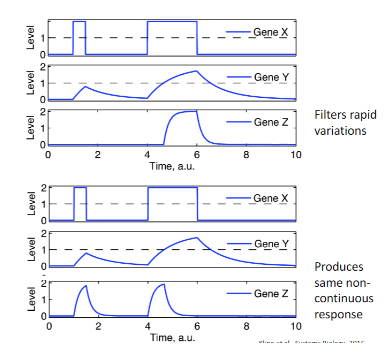
What type of network motif is shown by the bottom group of data?

incoherent feed-forward loop

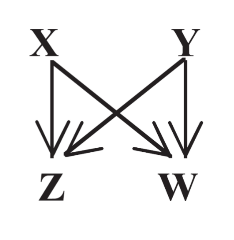
What type of forward network motif is shown here?

bi-fan

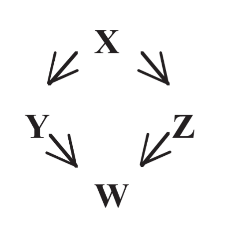
What type of forward network motif is shown here?

bi-parallel

Modular system

a system that consists of autonomous subsystems which perform specific functions

Robustness

the ability to maintain biological function despite perturbations; resistance to change/random forces

How does redundancy provide robustness?

By having several different pathways accomplish the same function; if one pathway fails then other pathways can compensate

Pareto optimality

the trade-off between multiple objectives

Pareto front

a boundary in which none of the objectives can be improved without compromising the other objectives

Select all parts of a systems model that are components:

• molecular species

• reaction catalysis

• rates of interactions

• ions

• chemical binding and unbinding

• regulation of activity

molecular species, ions

Select all parts of a systems model that are interactions:

• molecular species

• reaction catalysis

• rates of interactions

• ions

• chemical binding and unbinding

• regulation of activity

reaction catalysis, chemical binding and unbinding, regulation of activity

What are the kinetic assumptions needed for applying the law of mass action?

• rates depend on position in space

• individual reaction events cause infinitesimal changes in concentration

• fixed volume

• only a few molecules of each species present

• reaction volume is well stirred

individual reaction events cause infinitesimal changes in concentration, fixed volume, reaction volume is well stirred

The Law of Mass Action states that…
The _____ rate is proportional to the probability of a collision of the reactants

The _____ is proportional to the product of the concentrations of the reactants

reaction, probability

Differential Equation

an equation that relates one or more unknown functions and their derivatives

Ordinary Differential Equation

a differential equation dependent on only a single independent variable

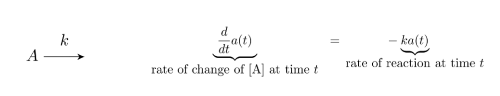
This equation models…

• decay

• production and decay

• irreversible conversion

• reversible conversion

• enzymatic reaction

• spatial reaction networks

• stochastic system

• predator-prey relationship (Lotka-Volterra)

decay

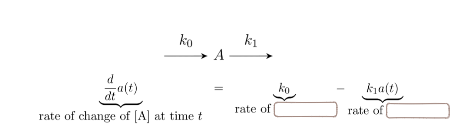
This equation models…

• decay

• production and decay

• irreversible conversion

• reversible conversion

• enzymatic reaction

• spatial reaction networks

• stochastic system

• predator-prey relationship (Lotka-Volterra)

production and decay

In this image, to calculate the steady state of a production/decay model, y is the rate of _____ and x is the rate of _____.

decay, production

This equation models…

• decay

• production and decay

• irreversible conversion

• reversible conversion

• enzymatic reaction

• spatial reaction networks

• stochastic system

• predator-prey relationship (Lotka-Volterra)

irreversible conversion

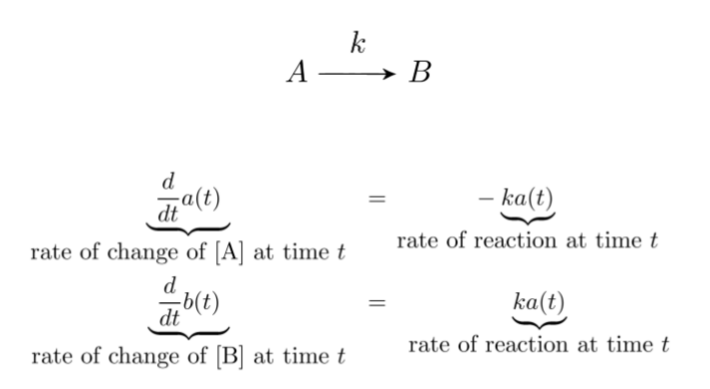
This equation models…

• decay

• production and decay

• irreversible conversion

• reversible conversion

• enzymatic reaction

• spatial reaction networks

• stochastic system

• predator-prey relationship (Lotka-Volterra)

reversible conversion

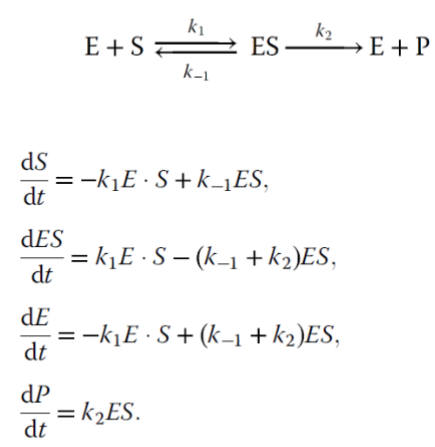
This equation models…

• decay

• production and decay

• irreversible conversion

• reversible conversion

• enzymatic reaction

• spatial reaction networks

• stochastic system

• predator-prey relationship (Lotka-Volterra)

enzymatic reaction

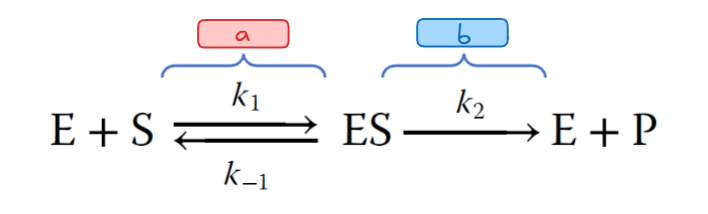
In the enzymatic reaction shown here, a represents _____.

enzyme binding

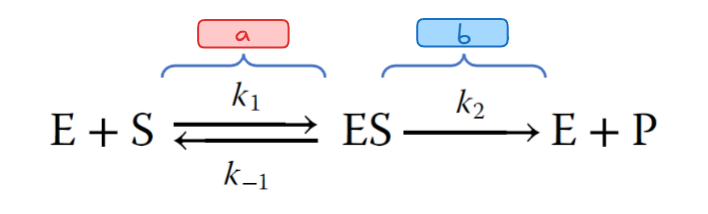
In the enzymatic reaction shown here, b represents _____.

enzyme catalysis

Maximal velocity

the maximal rate that can be attained when the enzyme is completely saturated with substrate

Michaelis constant

equal to substrate concentration that yields the half-maximal reaction rate

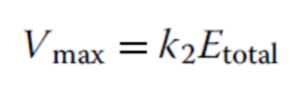
What does the equation shown here represent?

maximal velocity

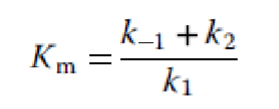
What does the equation shown here represent?

Michaelis constant

Michaelis-Menten Kinetics

a model of enzyme kinetics which explains how the rate of an enzyme-catalysed reaction depends on the concentration of the enzyme and its substrate

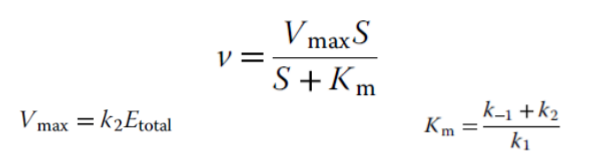
The equations shown here are used for what type of model?

Michaelis-Menten kinetics

Euler’s Method

a method for solving ODEs with a given initial value; produces approximate values at a discrete collection of time-points

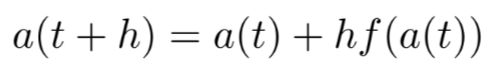
What is the equation shown here used for?

Euler’s method of solving ODEs

Spatially distributed dynamic behavior can be modeled with which type of equations?

• differential equations

• ordinary differential equations

• partial differential equations

partial differential equations

Partial Differential Equation

an equation that relates one or more unknown functions and their derivatives to time and space

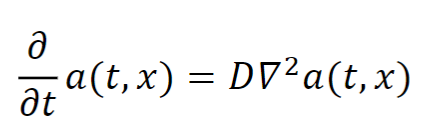
This equation models…

• decay

• production and decay

• irreversible conversion

• reversible conversion

• enzymatic reaction

• spatial reaction networks

• stochastic system

• predator-prey relationship (Lotka-Volterra)

spatial reaction networks

Intrinsic Noise

noise from within the system; caused by the probabilistic character of (bio)chemical reactions

Extrinsic Noise

noise from within outside the studied system; caused by random fluctuations in environmental parameters

Stochastic Differential Equation

a differential equation that accounts for the presence of noise affecting the results

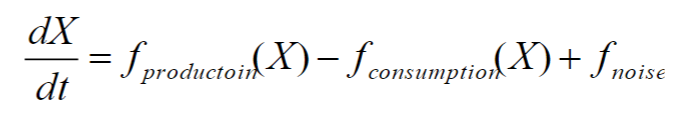
This equation models…

• decay

• production and decay

• irreversible conversion

• reversible conversion

• enzymatic reaction

• spatial reaction networks

• stochastic system

• predator-prey relationship (Lotka-Volterra)

stochastic system

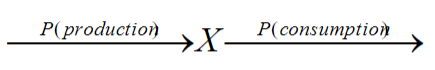
This reaction models…

• decay

• production and decay

• irreversible conversion

• reversible conversion

• enzymatic reaction

• spatial reaction networks

• stochastic system

• predator-prey relationship (Lotka-Volterra)

stochastic system

Stochastic simulations with continuous variables can be modeled using the _____.

Langevin approach

Stochastic simulations with discrete variables can be modeled using the _____.

Gillespie algorithm

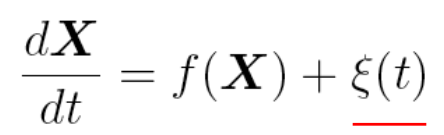
What equation is shown here?

Langevin stochastic differential equation

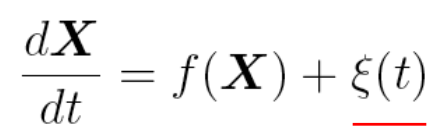
In the Langevin stochastic differential equation, what does the term ξ(t) mean?

noise term

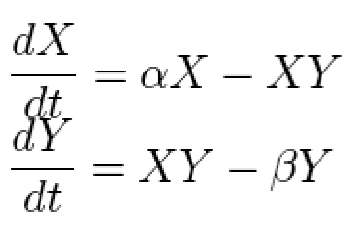
These equations model…

• decay

• production and decay

• irreversible conversion

• reversible conversion

• enzymatic reaction

• spatial reaction networks

• stochastic system

• predator-prey relationship (Lotka-Volterra)

predator-prey relationship (Lotka-Volterra)

Parameter Estimation

the method of finding a set of parameters that minimizes the difference between experimental data and model prediction

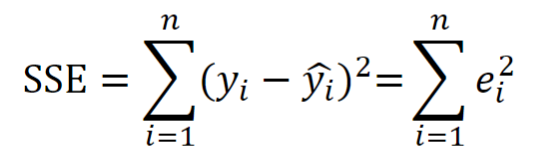
The Sum of Squared Errors equation, shown here, is used for…

parameter estimation

Linear regression can be used for some nonlinear functions, but only under what circumstances?

the function permits a mathematical transformation that makes them linear