Control to memorise

3 Key properties of Linear time invariant systme

1. obey principle of superposition (x1+x2)→(y1+y2)

2. homogeneity (Ax→Ay)

3. time invariance( x (t-T)→y (t-T) )

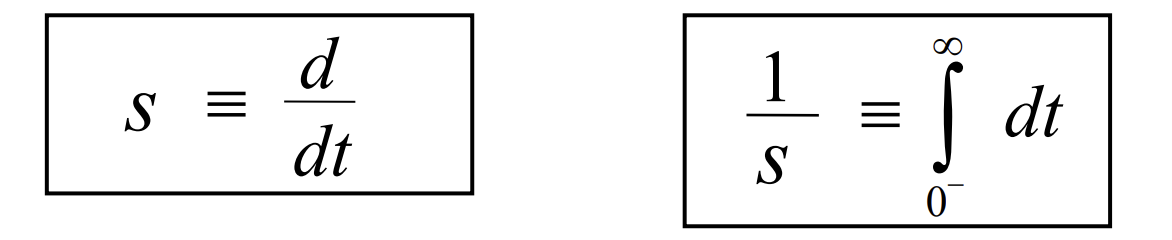
Laplace of derivative and integral

Basic transfer function system

Calcuating >1 resistor, inductor and capacitor relationship

Equation for damping force

Standard form transfer function of first order systems

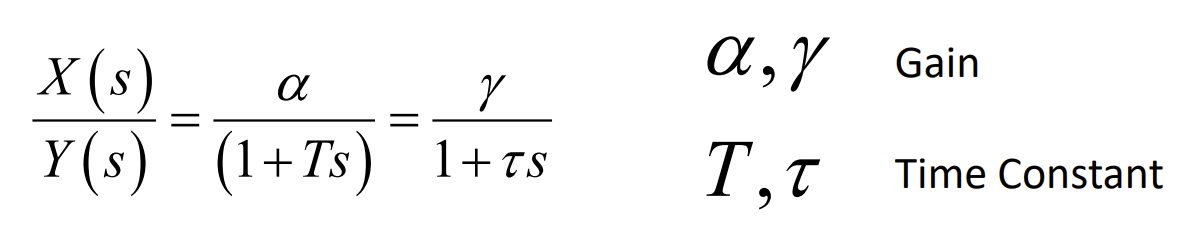
Standard form transfer function of second order system

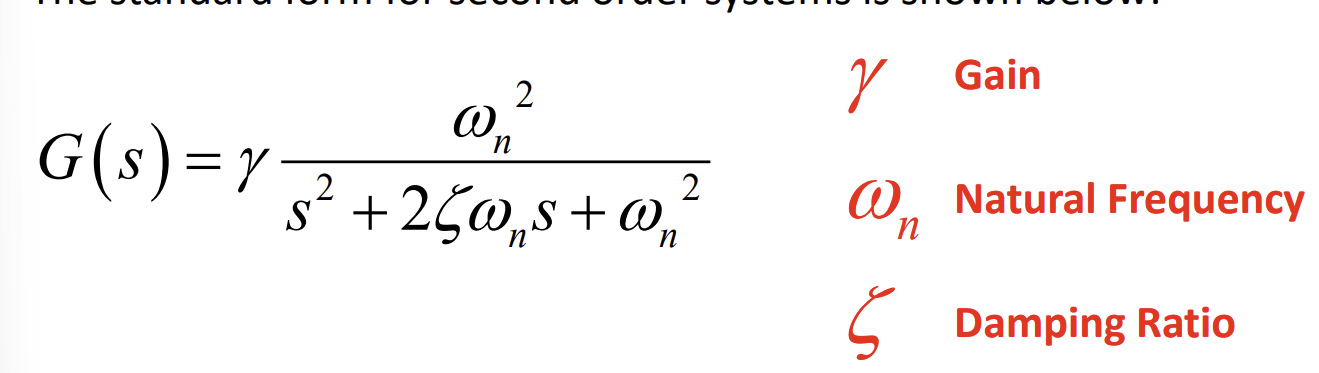
time domain of a second order transfer function

assuming its underdamped

Input functions

Characteristics of first order system step response

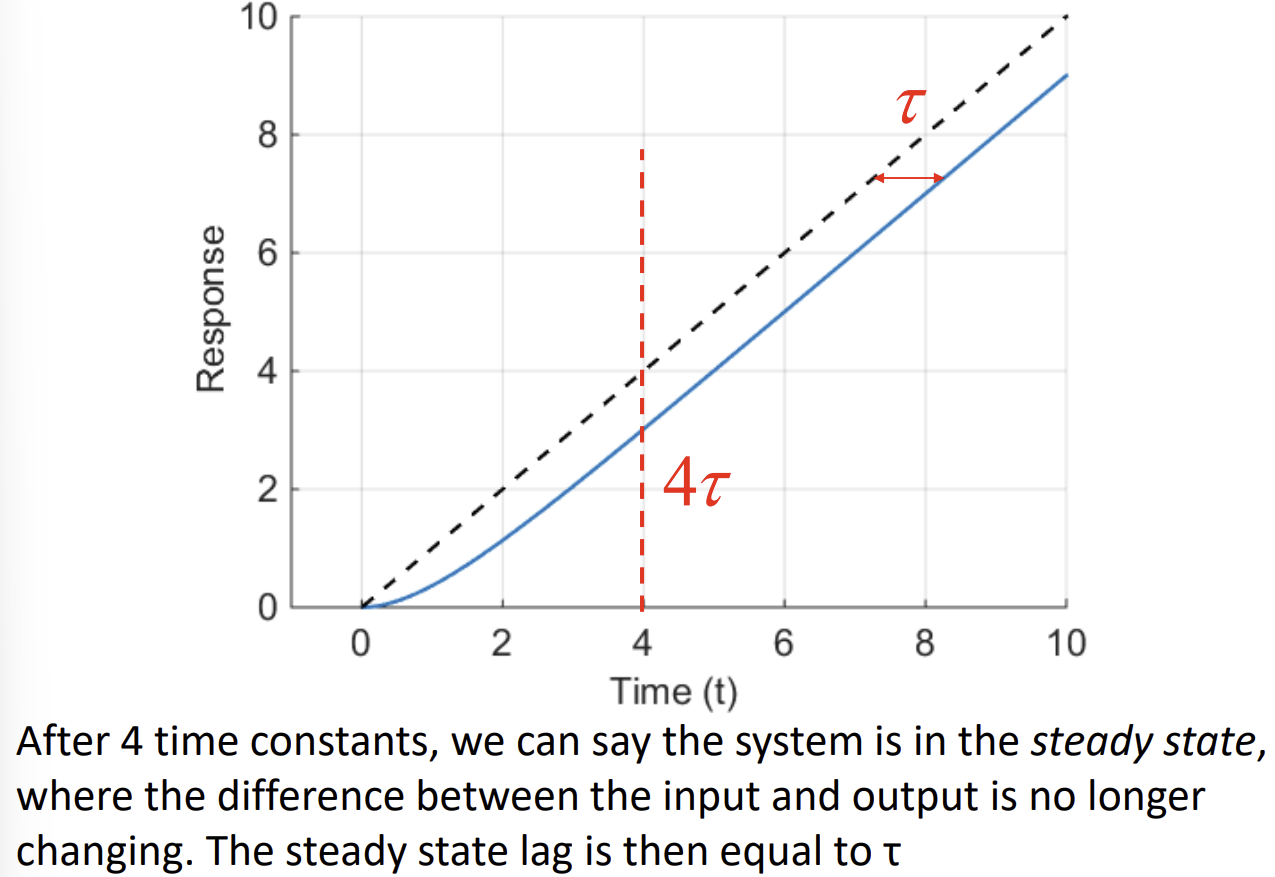
Characteristics of first order system ramp response

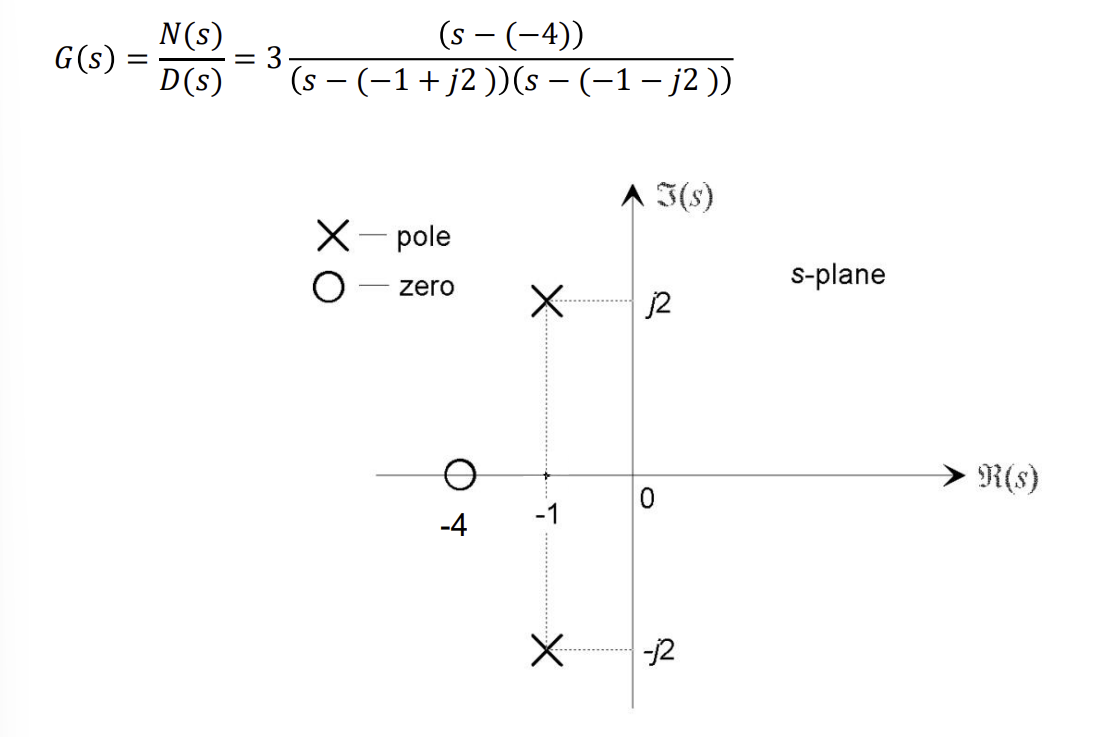
Definition of poles and zeros

roots of transfer function

numerator: zeros

denominator: poles

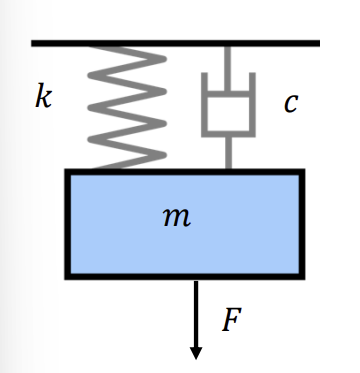
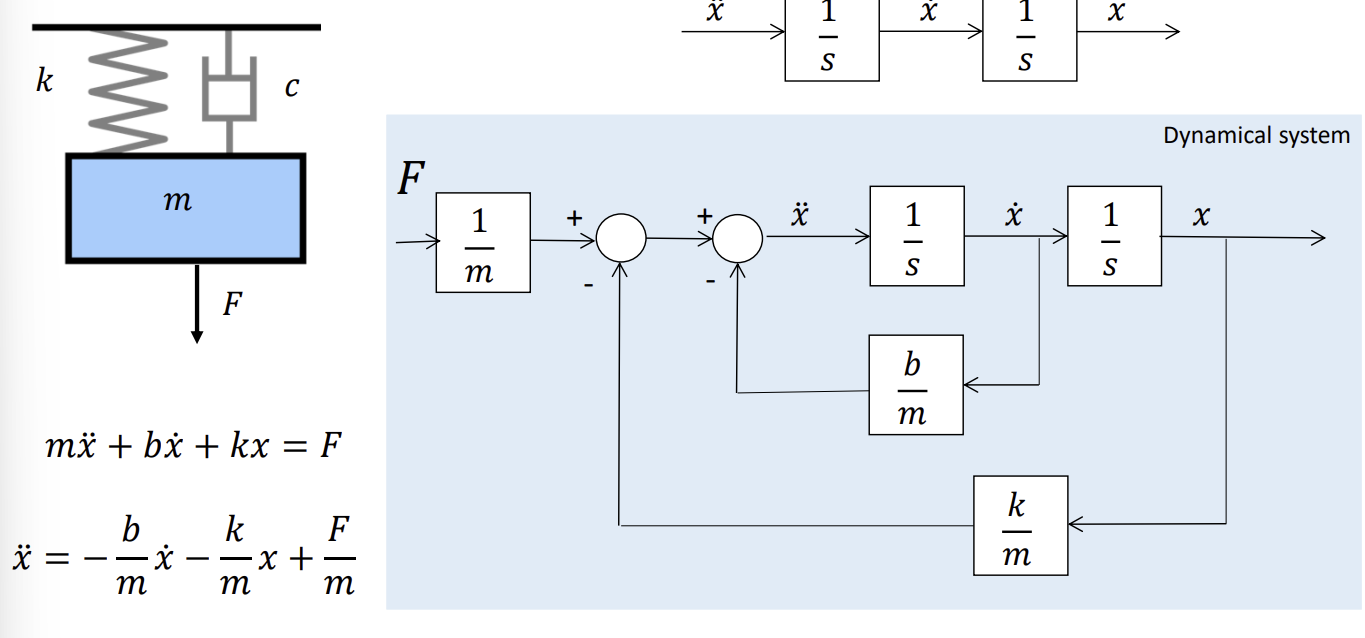
Block diagram for this system

Characteristic of an underdamped 2nd order system

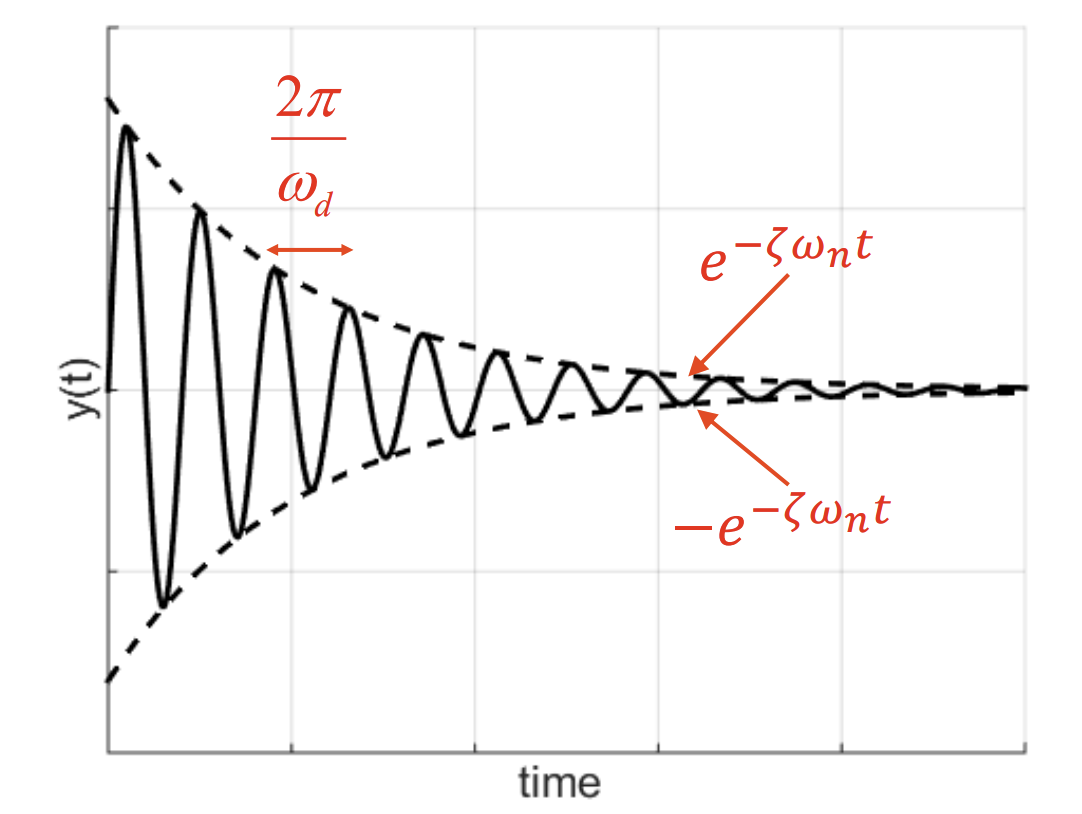
Relationship between damping ratio and characteristic equation of s

Characteristics of critically damped 2nd order system

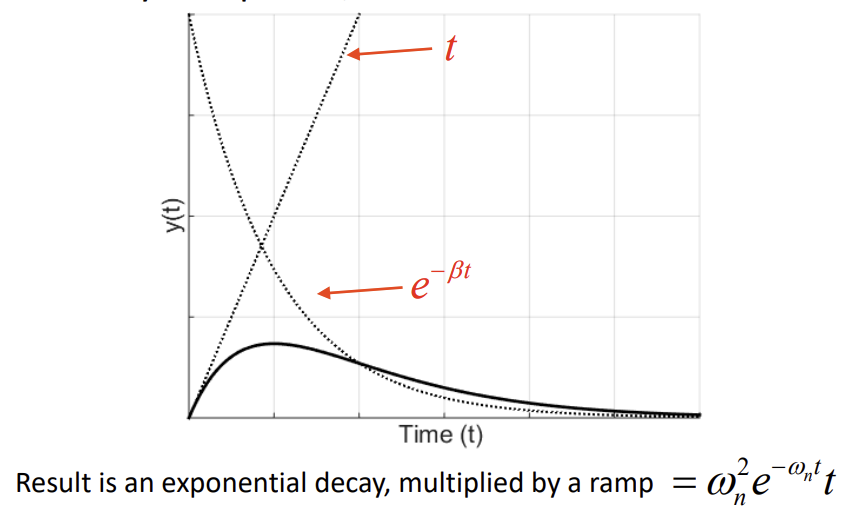
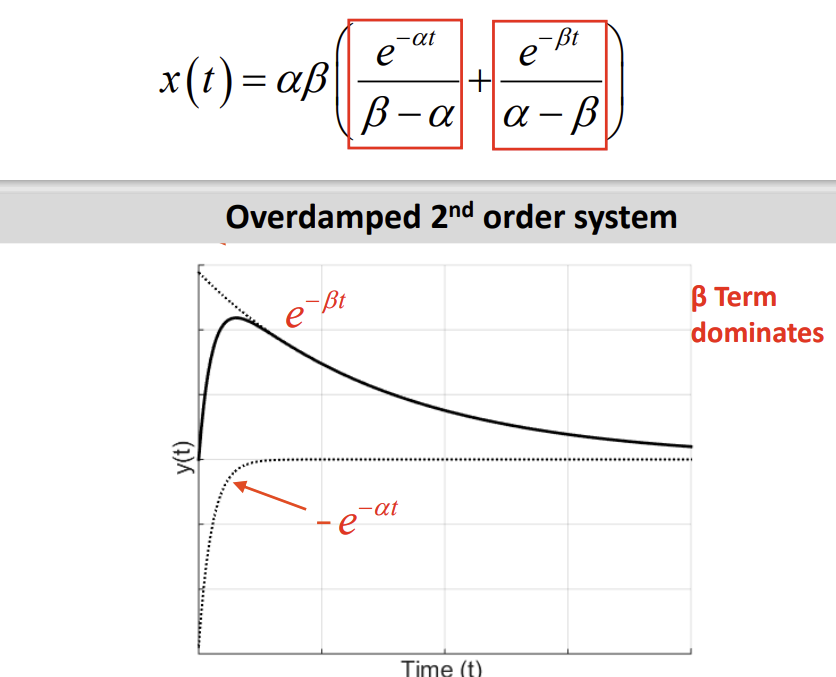
Characteristic of a overdamped 2nd order system

• right most pole dominates response

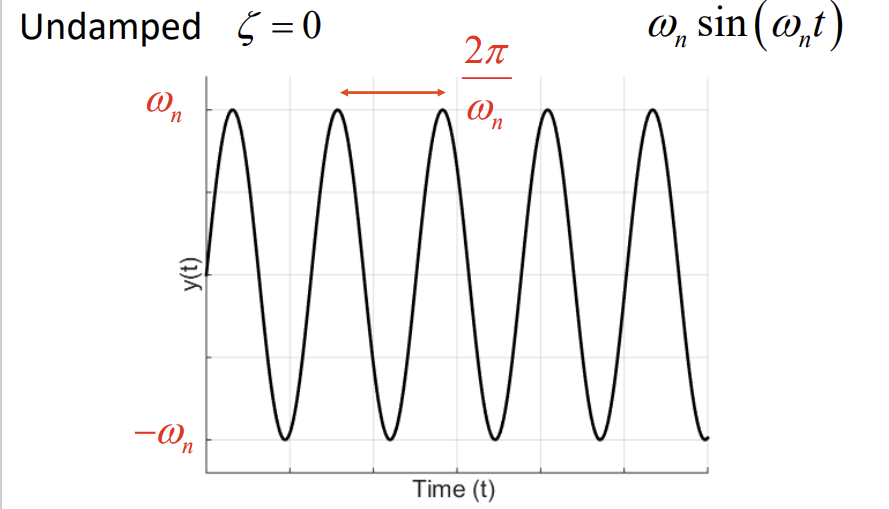
Characteristic of an undamped 2nd order system

Definition and formula of rise time

Time to reach steady state value (for first time)

• can be read from graph

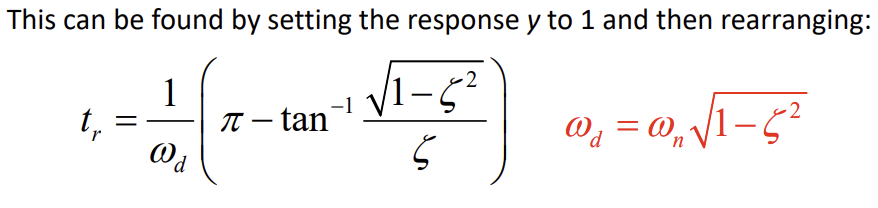
Definition and formula of peak time

Time where y value is maximum

• occur at T/2

• or dydt=0 for the first maximum value

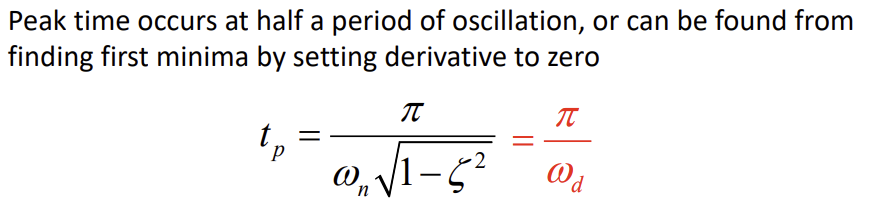
Definition and formula of overshoot

y(t_p)-t(t_ss)

• can be rearranged to find damping ratio required for overshoot

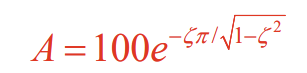
Definition and formula of settling time

• time where y begins to settle around 2 or 5% of its SS value

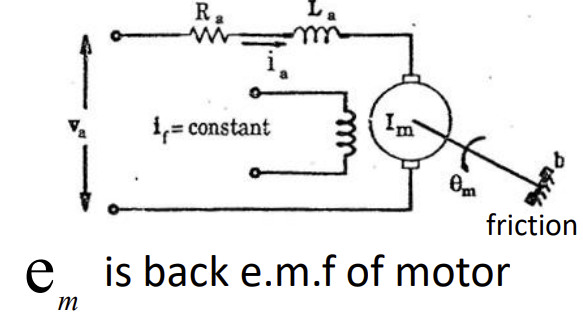
Calculation of voltage in a circuit in laplace

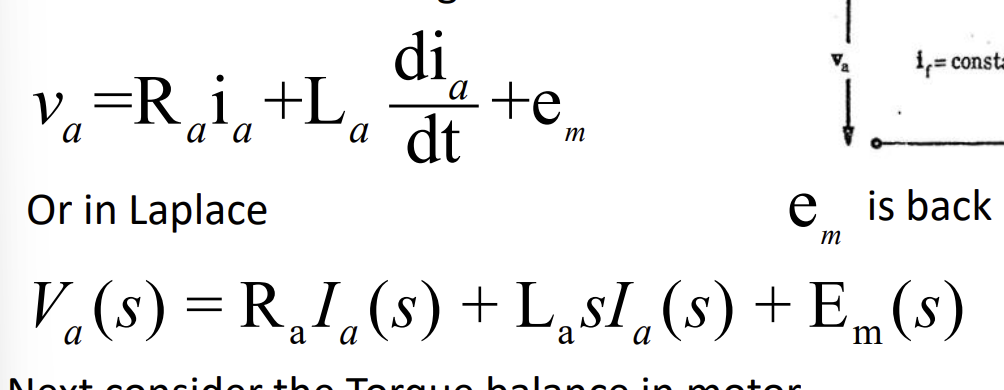
Calculation of torque in a motor, with friction b and inertia I

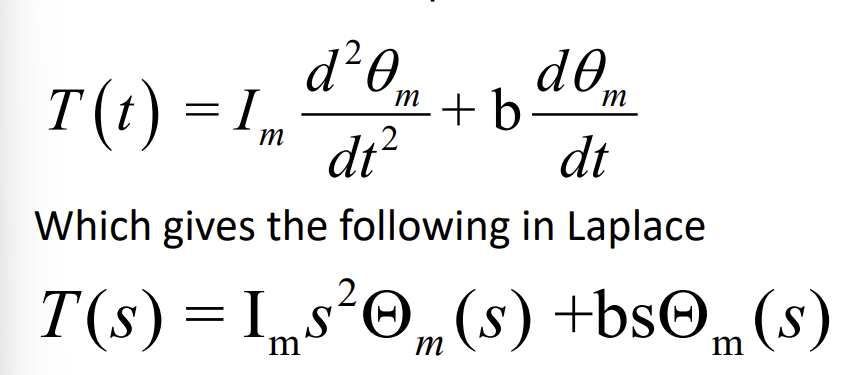
Ramp input for a first order system*s

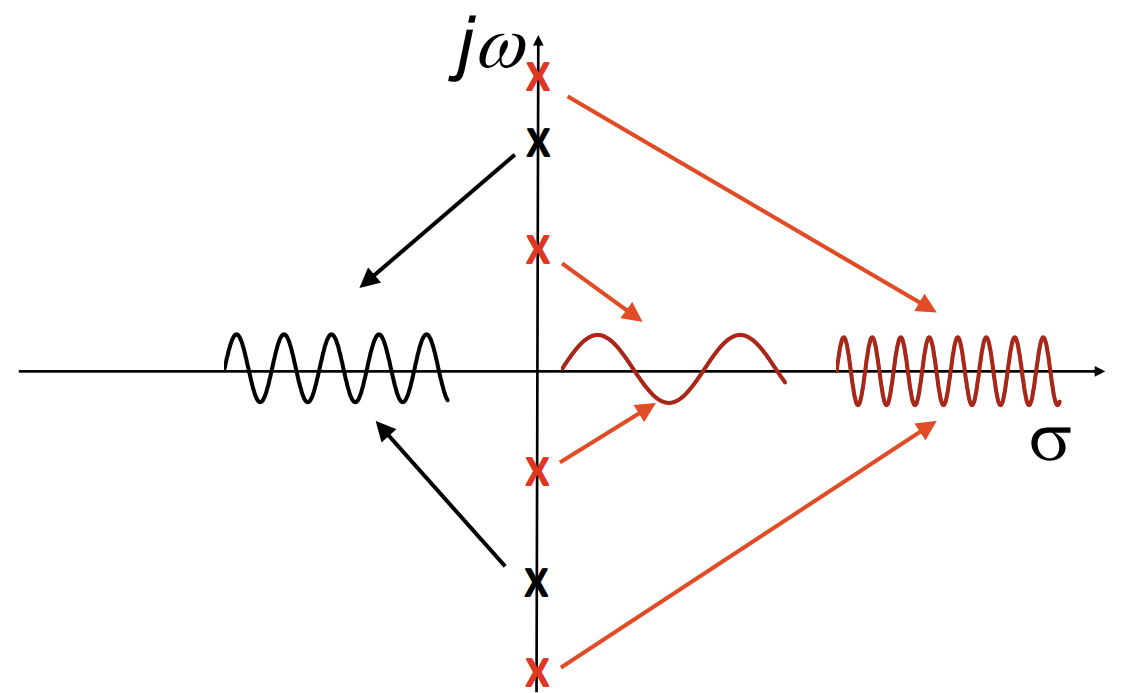
changes in graph in s plane, through the real axis

larger magnitude→ faster increase or decay

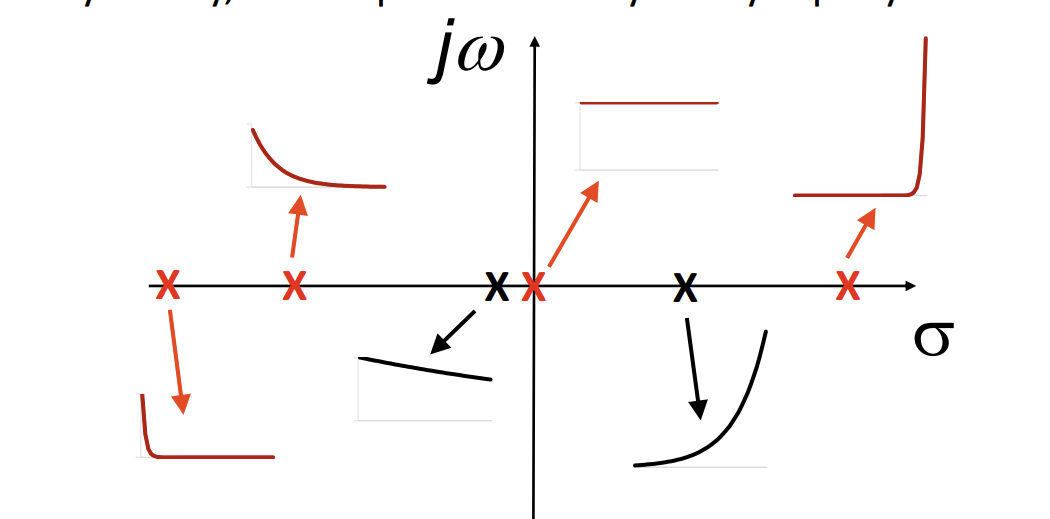
changes in graph in s plane, through the imaginary axis

larger magnitude-smaller period

Final Value Theorem

final value reached when t→ infinity

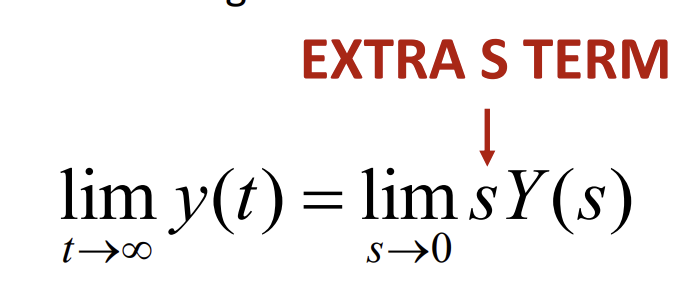
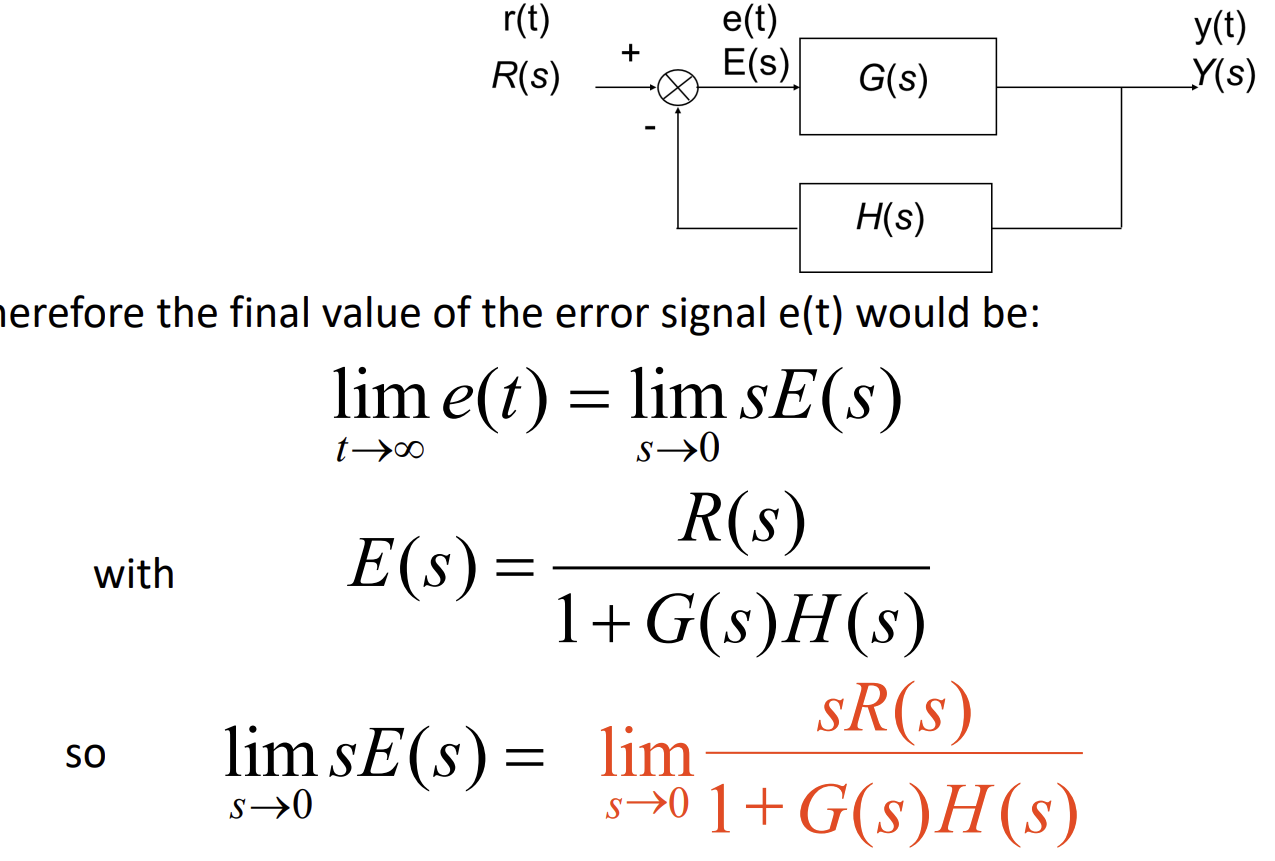
Equation to find final value of steady state error

Steady state position error formula

SSE for step input

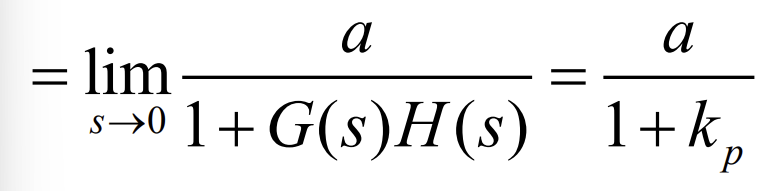
Formula of position error constant

amount of steady state error of the system when stimulated by a unit input

Definition and formula of steady state velocity lag

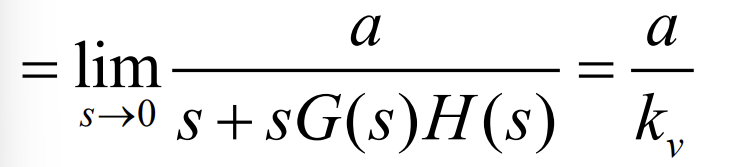
Formula and definition of velocity error constant

amount of steady state error when the system is stimulated with a ramp input

Determining system type

depends on number of poles at origin

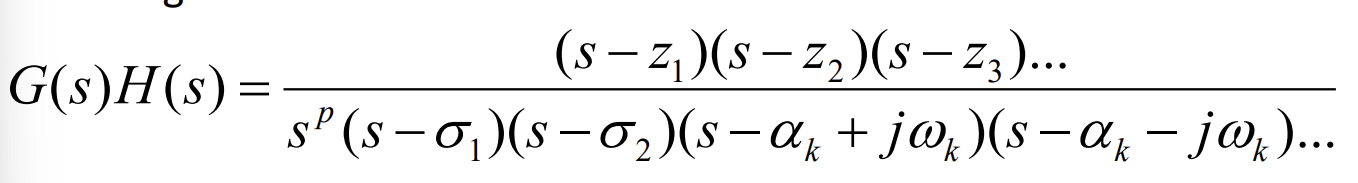
Relationship of pole with SSE

Relationship of proportional gain to behaviour of system

• adjust system to reach steady state as soon as possible

• inertia leads to large overshoot

Relationship of derivative gain to behaviour of system

Improve transient response by resisting overshoot

SSVL remain unchanged

Relationship of integral gain to behaviour of system

• decrease or remove SSE

• increase type (P+1)

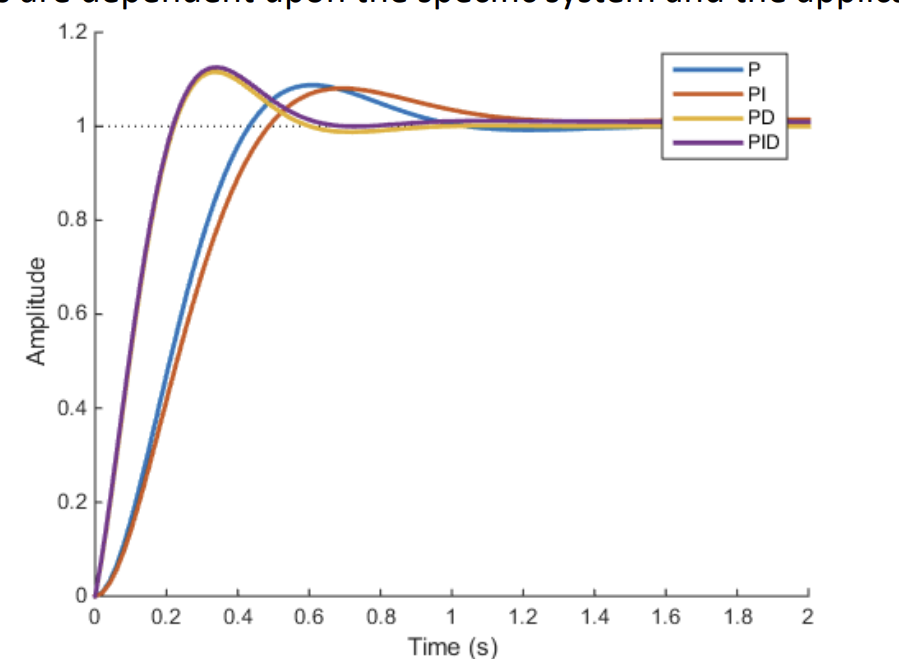
Observation of each gain

1. PI

• little effect on transient response

• as it is a type one system with step input, already has no steady state

2. PD

• improve transient response

• allow greater proportional gain to be used while still minimising overshoot