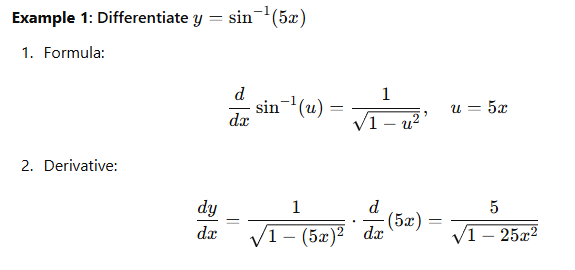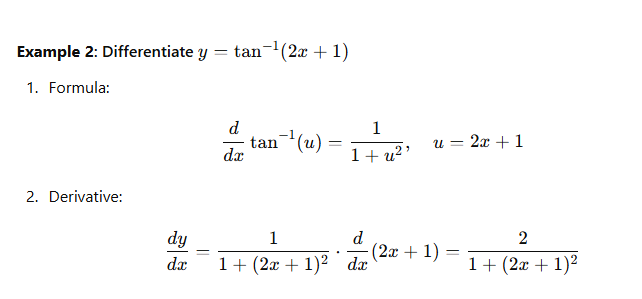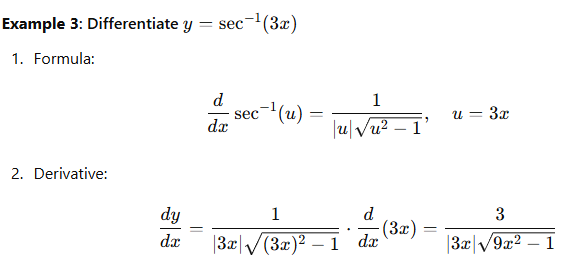Introduction

Inverse trigonometric functions are fundamental tools in calculus, extending the applications of trigonometry to areas involving rates of change, integration, and modeling. Functions like arcsine, arccosine, and arctangent are widely used to describe relationships between angles and sides of triangles, especially when standard trigonometric functions are inverted to solve for an angle. Differentiating these functions is an essential skill, helping us analyze how these relationships change with respect to variables.

In this note, we will explore the differentiation of inverse trigonometric functions in detail. The section includes their formulas, the step-by-step procedure for differentiation, applications of the chain rule, and example problems. Whether you are a student preparing for exams or someone looking to strengthen your calculus foundations, this comprehensive guide will provide clarity and confidence in tackling these derivatives.

Differentiation Formulas

Each of the six inverse trigonometric functions has a unique derivative formula that you need to memorize and understand. These formulas are derived from the geometric and algebraic definitions of the inverse functions.

These formulas form the backbone of differentiation for inverse trigonometric functions. Memorizing them is a key step in solving problems efficiently.

Steps for Differentiation

To differentiate a function involving an inverse trigonometric component, follow these steps:

1. Recognize the Function: Identify the inverse trigonometric function present in the given problem.

2. Recall the Formula: Write down the corresponding derivative formula for the identified function.

3. Simplify the Argument: If the function's argument is more complex than xxx, simplify it if possible.

4. Apply the Chain Rule: For arguments other than xxx, multiply the derivative of the inverse function by the derivative of the argument.

5. Simplify the Result: Reduce the expression to its simplest form, ensuring clarity and correctness.

Examples

Applications

The differentiation of inverse trigonometric functions finds applications in many fields:

• Physics: To model rotational motion and waveforms.

• Engineering: To analyze signal processing and structural angles.

• Geometry: To solve problems involving angles and distances.

• Integration: As a basis for solving integrals involving inverse trigonometric expressions.

Conclusion

Differentiating inverse trigonometric functions is a critical skill in calculus, offering insights into the rates of change of complex angular relationships. By mastering the formulas and applying the chain rule effectively, you can confidently solve problems involving arcsine, arccosine, and other inverse functions. Beyond academic use, these derivatives play a vital role in scientific and engineering computations, proving their importance across disciplines. With consistent practice and application, you’ll gain both understanding and efficiency in working with these functions.