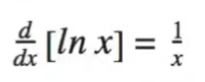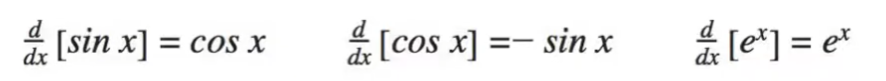Unit 2: Differentiation: Definition and Fundamental Properties
Rates of Change
We know that there are two ways of finding the rate of change
We can use the difference quotient to find the Average Rate of Change
The difference quotient is the rate of change over an interval of time
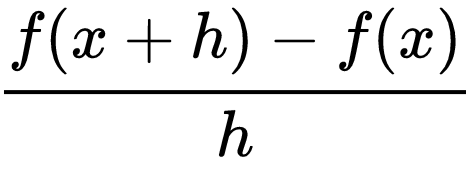
A simpler way of saying this is y2 - y1/x2-x1
The other way of finding the rate of change is at a specific point in time and this is called the Instantaneous Rate of Change
This is the difference quotient but with a limit as h → 0
Slopes of Lines & Definition of Derivative
Let’s say we had a line that isn’t linear, and we want to find the slope
For a linear line, the slope is “rise over run” but we can’t do that for a curved line
Therefore we have to use the secant line to approximate the slope
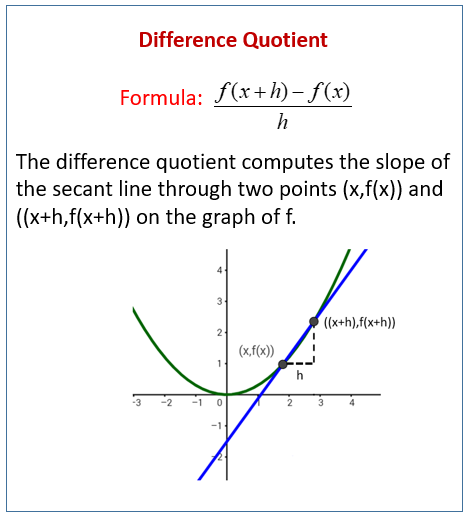
We can find the slope of the secant line using the difference quotient!
- (Look at the formula above)
The closer the points are, the more accurate this slope will be
Therefore we can use a different kind of line- the tangent line- that touches the curve at exactly one point
We get this line by using the Instantaneous Rate of Change (remember: the difference quotient but with a limit as h → 0)

This is called the definition of the derivative!
- Remember that the derivative is just the rate of change at a specific point, so we use a limit to find the slope as x gets infinitesimally small
Derivative Notation
| Function: | First Derivative: | Second Derivative: |
|---|---|---|
| f(x) | f’(x) | f'“(x) |
| g(x) | g’(x) | g”(x) |
| y | y’ or dy/dx | y” |
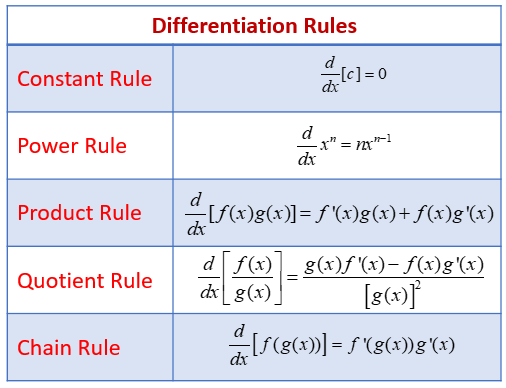
Derivative Rules
Using the limit definition of the derivative is tedious, so we have rules that can make taking a derivative easier!
Constant Rule: If f(x) = k where k is a constant then f’(x) = 0
- Ex. f(x) = 10 so f’(x) = 0
Constant Multiple Rule: If you have a constant multiplied by a function, you can “pull the constant out”
- So [k * f(x)]’ would be the same as k * f’(x)
The Power Rule: If f(x) = x^n then f’(x) = nx^n-1
- For example x^4 becomes 4x^3 and 2x^2 would be 4x
- A good way to describe this rule is to “multiply down and decrease the power”
- The power rule works for polynomials!
The Product Rule: If you have two polynomials multiplied by each other like (2x +7)(9x + 8) you could multiply it out and then use the power rule, but this takes time, so we have something called the product rule.
- The product rule says that if f(x) = uv then f’(x) = (u)(dv/dx) + (v)(du/dx)
- You take the first term and multiply it by the derivative of the second term (using the power rule) then add that to the second term multiplied by the derivative of the first term
- The way I learned it was “1d2 + 2d1” (first * derivative of second + second * derivative of the first)
The Quotient Rule: If you need to take the derivative of a fraction, you have to use this rule
- The Quotient Rule says that if f(x) = u/v then f’(x) = (v)(du/dx) - u(dv/dx) / v^2
- You take the denominator and multiply it by the derivative of the numerator, then subtract the numerator multiplied by the derivative of the denominator all over the denominator squared
- The way I learned it was “low d high - high d low/ low^2” (low * derivative of high - high * derivative of low over low^2)
The last set of things that you have to know are “memory derivatives” or things that are easier to memorize than to derive. These will be the derivatives of sinx, cosx, e^x, and lnx