IB math aa hl 1 formulas sem 1

Vertex/completed square form

vertex at h,k

axis of sym at h

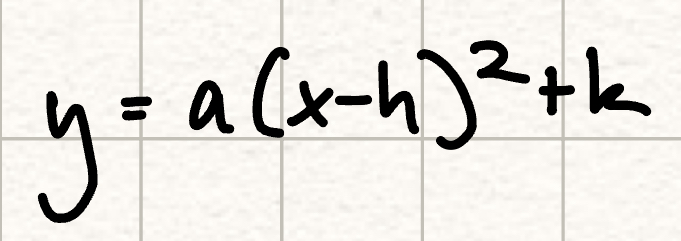
axis of symmetry (standard form)

completing the square

Discriminant

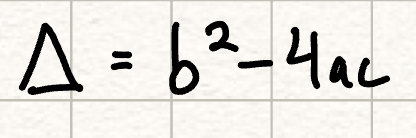
2 real solutions

1 real solution

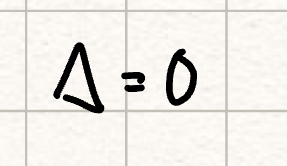
2 imaginary/complex solutions

positive definite

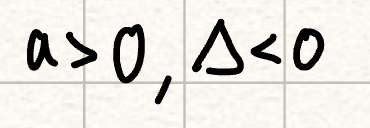
Negative definite

Y-int in fully factored form

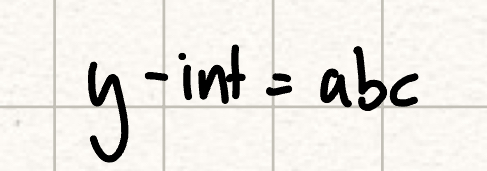
Fully factored form

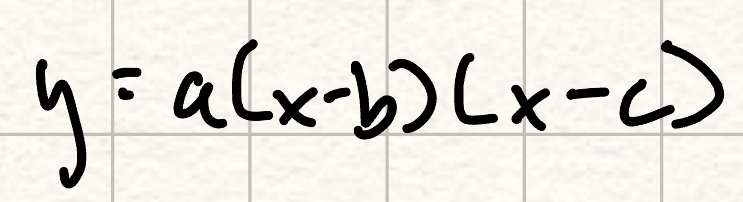
Sum of roots

Product of roots

root a • root b

root a / root b

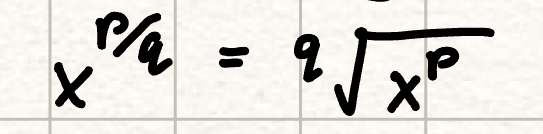
x^p/q

Vertical shift (exponential functions)

affects whole y

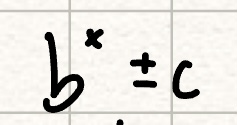
horizontal shift

affects just x, goes in the opposite way you think

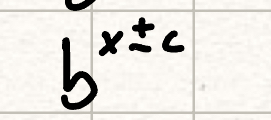
flip across the y axis (exponential functions)

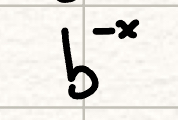
flip across x axis (exponential functions)

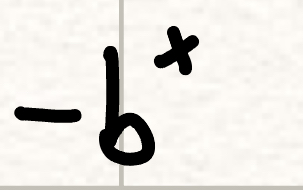
log m + log n

log (mn)

mlogb

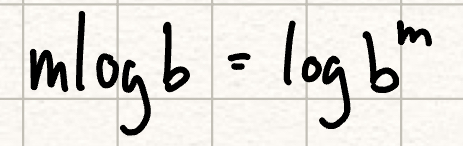
b^(log(sub b)a

a

vertical stretch by k

vertical shift by k

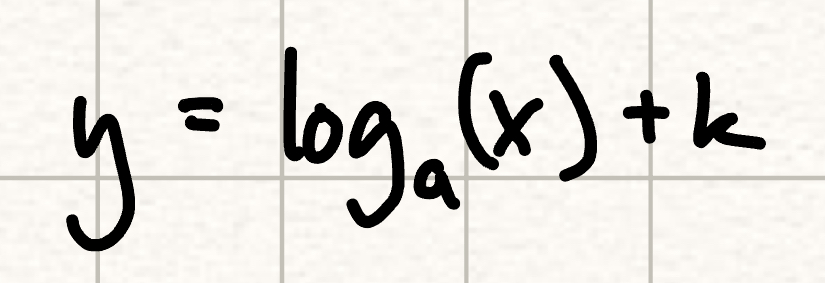
horizontal stretch by (1/k)

horizontal shift by k units left

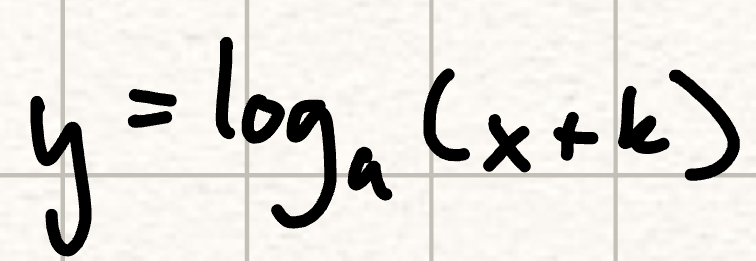
change of base rule logs

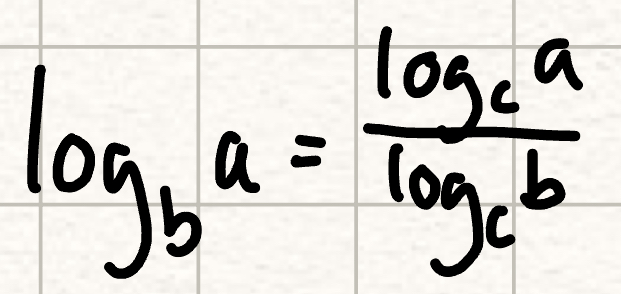
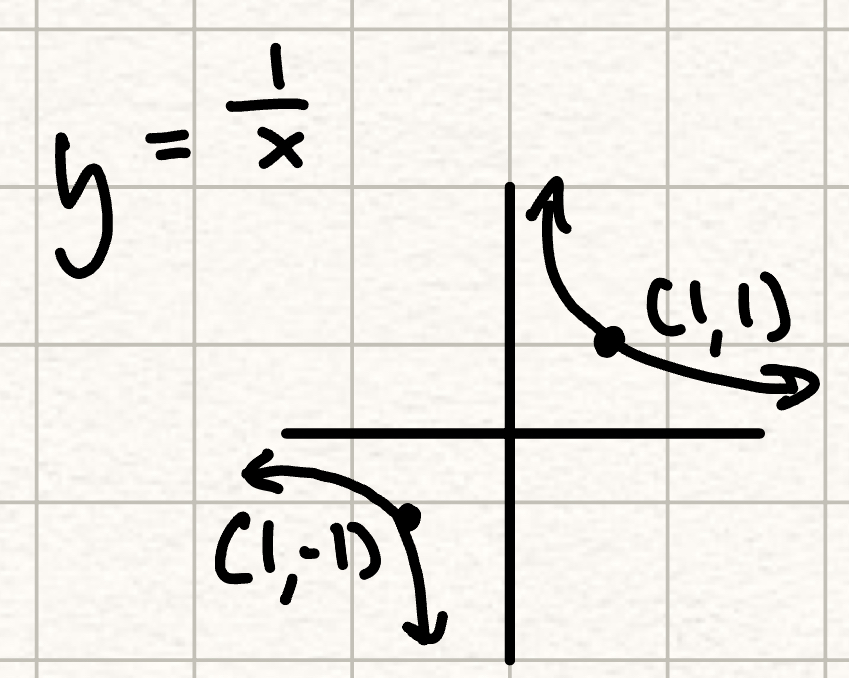
y= (1/x)

points at (1,1) and (-1,-1)

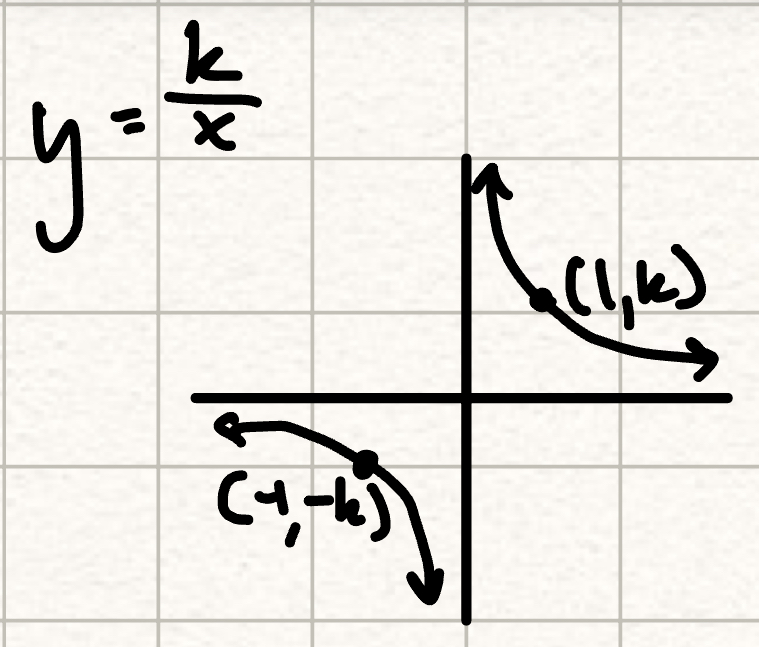
y = (k/x)

points at (1,k) and (-1,k)

y = 1/x²

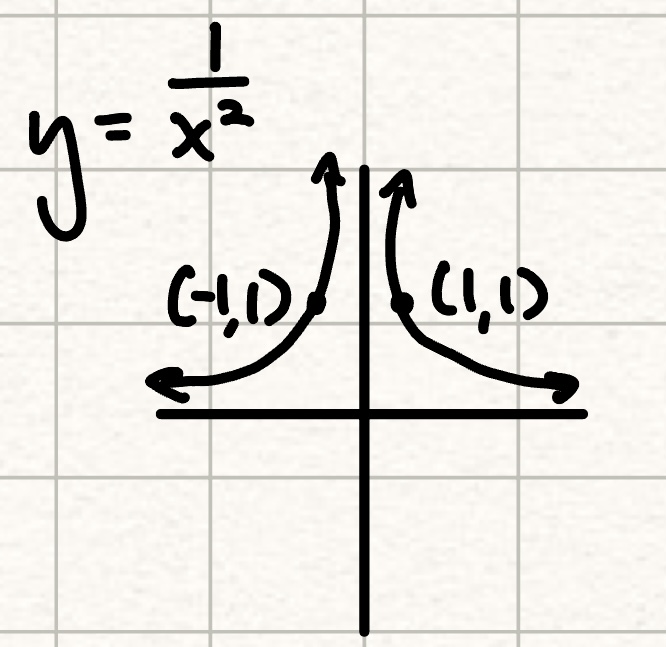
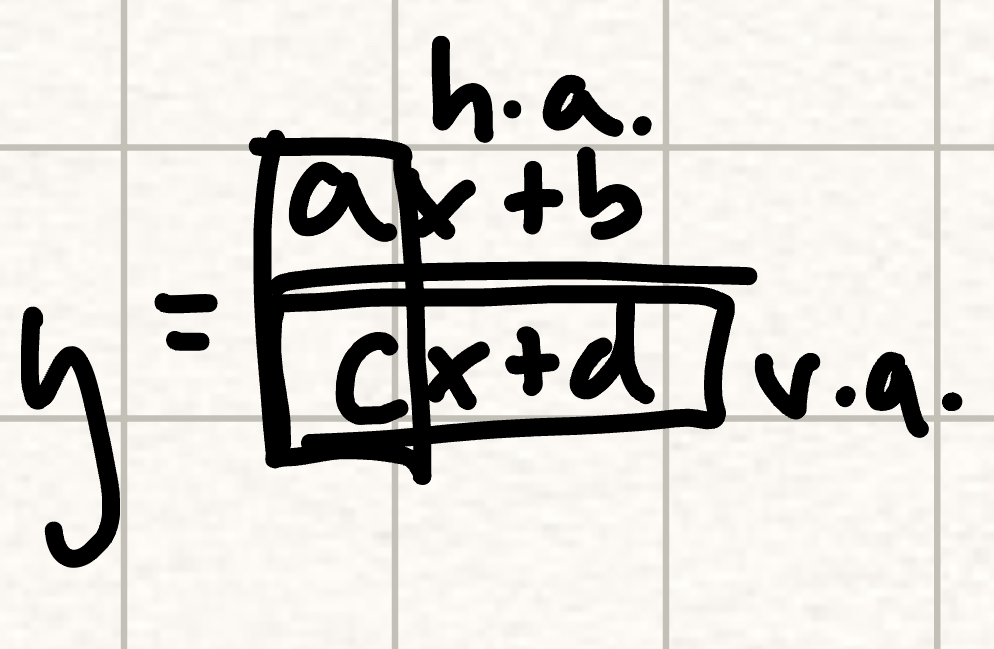
horizontal and vertical asymptotes of a rational function

even function

function doesn’t change with a -x

odd function

-x turns entire function negative

f(x) transformed by vector (a b)

nCr

remember r!(n-r)!

general term formula

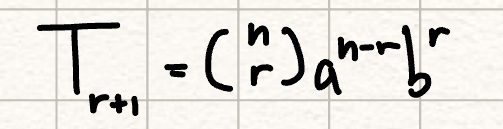
nth term formula (arithmetic)

nth term formula (geometric)

sum of arithmetic sequence (given un)

sum of arithmetic sequence

sigma notation

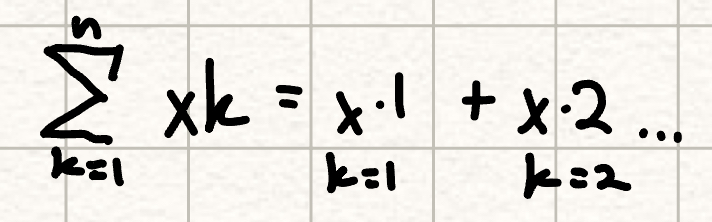
sum of infinite geometric

sum of finite geometric