AP STATS: Chapter 8

Confidence interval general formula

Point estimate ± margin of error

Point estimate equation

A+B/2

M.E. equation

B-A/2

Confidence interval interpretation

“We are ___% confident that the interval from A to B captures the true parameter with context”

Standard error equation

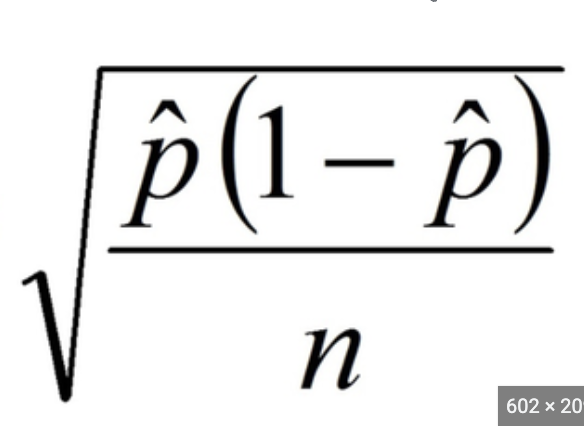
Confidence level interpretation

“If we take many, many samples and calculate a confidence interval for each one, about % of them will capture the true parameter with context”

as confidence level increases

me increases

as me increases

confidence level increases

as sample size increases

me decreases

as me decreases

sample size increases

conditions

random, 10%, LCC

random verifies

generalize population

10% verifies

independence: in sampling with out replacement. helps to not have biased results, you can use certain equations

LCC verifies

to assume sampling distribution is approximately normal, to find z critical in interval

critical value x standard error

margin of error

specific formula

(p) choose:

procedure: one-sample z-interval for p

define p (the parameter)

state confidence level

calculate

write formulas, plug in values, calculate CI

Conclusion

we are _% confident…”

find sample size

ME=z* x sq root p(1-p)/n

if we dont know p hat, use

0.5

if n is a decimal

round up

choose p1-p2

two-sample z-interval for p1-p2

define p1-p2

state confidence level

check p1-p2

independent random samples or random assignment+ 10+LCC

calculate p1-p2

evaluate a claim

(+,+) 1st proportion is greater

(-,-) 1st proportion is smaller

(-,+) no evidence of difference (0)

rate of increase me-n

quadruple to halve, me is proportional to 1/sq of n