Set Theory Concepts: Types, Notation, Operations, and Venn Diagrams

Set

A well-defined collection of distinct objects.

two types of sets

Universal set (mother set) and subset.

How is a set denoted

By capital letters.

difference between a set and a non-set

A set contains distinct elements, while a collection with repeated elements or improper descriptions is not a set.

cardinality

The number of elements in a set, denoted as n(A) for set A.

What is a null set?

A set with no elements, denoted as ∅ or {}.

What is the cardinality of a null set?

Zero (0).

What is the difference between finite and infinite sets?

Finite sets have a countable number of elements, while infinite sets have an uncountable number of elements.

What is a subset?

Set A is a subset of set B if every element of A is also an element of B, denoted as A ⊆ B.

What is the notation for a proper subset?

A ⊂ B, meaning all elements in A are in B, but not vice versa.

What are equivalent sets?

Two sets are equivalent if they have the same number of elements, denoted as A ≈ B.

What is the notation for the complement of a set?

The complement of set A is denoted by A'.

What does the union of two sets represent?

The union of sets A and B (A ∪ B) contains all elements that are in A, in B, or in both.

What does the intersection of two sets represent?

The intersection of sets A and B (A ∩ B) contains all elements that are in both A and B.

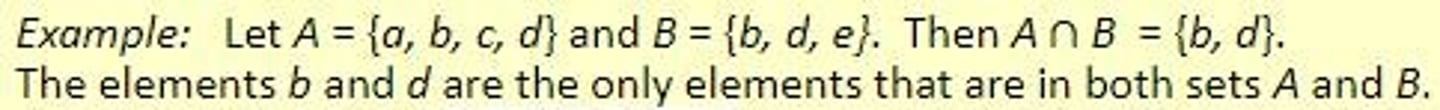
What is De Morgan's Theorem?

It describes the relationship between the complement of unions and intersections of sets.

What is the formula for the number of subsets of a set?

The total number of subsets is 2^n, where n is the number of elements in the set.

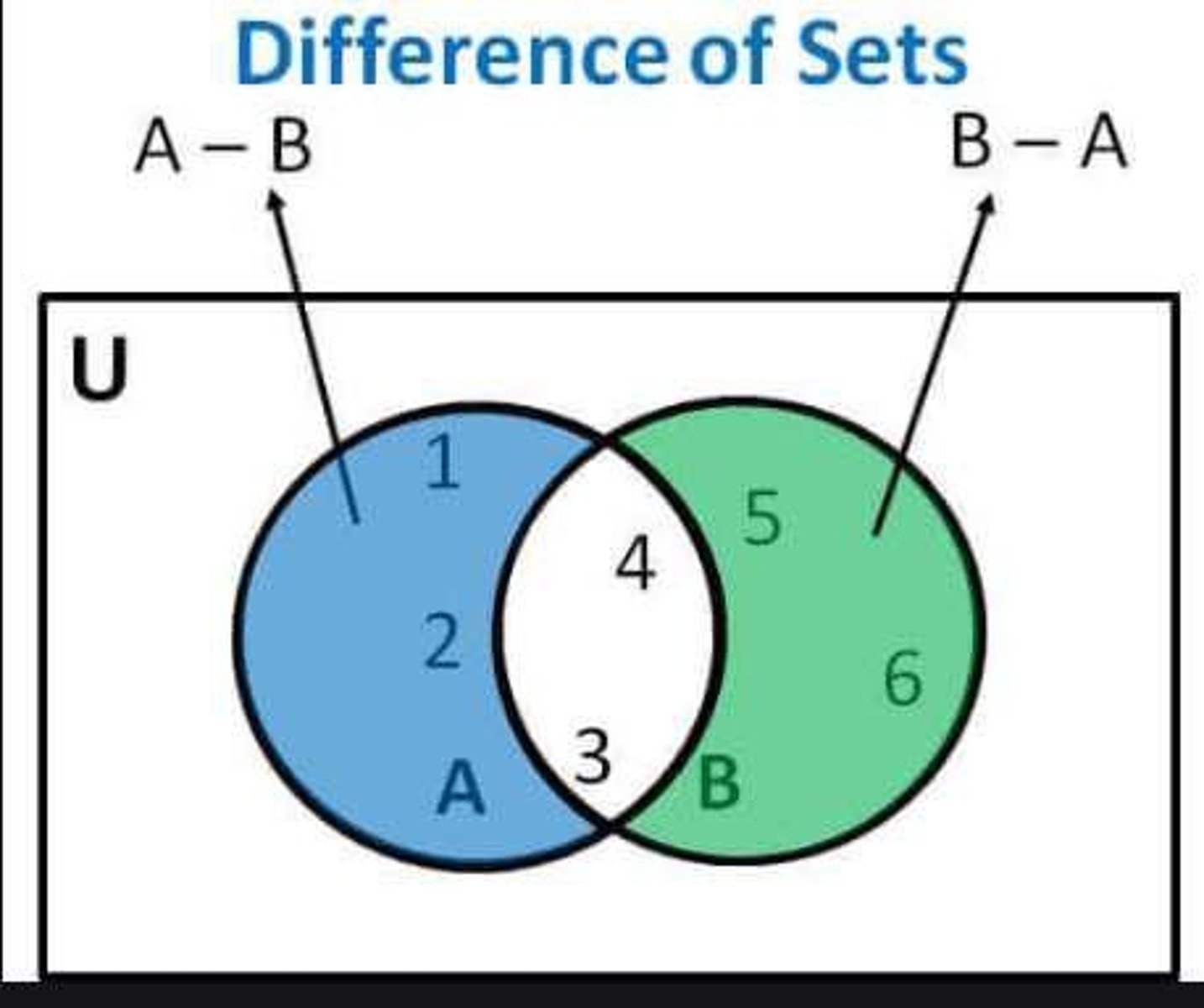
How do you find the difference of two sets?

The difference A - B contains elements in A that are not in B.

What is the significance of the universal set?

It contains all possible elements under consideration for a particular discussion or problem.

What is the notation for the cardinality of the union of two sets?

n(A ∪ B) = n(A) + n(B) - n(A ∩ B).

What is the formula for finding the number of proper subsets?

The total number of proper subsets is 2^n - 1.

What does it mean if two sets are equal?

Sets A and B are equal if they have exactly the same elements.

What is the significance of the empty set in relation to subsets?

The empty set is a subset of every set.

What is the complement of the universal set?

The complement of the universal set is the empty set.

How do you denote the cardinality of an infinite set?

An infinite set is denoted as having cardinality n(A) = ∞.

What is the relationship between equivalent sets and equal sets?

Equivalent sets have the same number of elements, while equal sets have the same elements.

What is the notation for the complement of a set A?

A' (A prime).

What does the notation A ∩ B' represent?

It represents the intersection of set A and the complement of set B.