Chapter 6 Networking Optimization Problems单词卡 | Quizlet

e. All of the answer choices are true.

In a minimum-cost flow problem, which of the following is TRUE?

a. There is at least one supply node.

b. There is at least one demand node.

c. A feasible solution will exist if and only if total supply matches total demand.

d. The number of supply nodes can be different from the number of demand nodes.

e. All of the answer choices are true.

c. a transshipment node.

In a distribution network, a warehouse which takes in goods from a manufacturing site and ships goods to customers is represented by

a. a supply node.

b. a demand node.

c. a transshipment node.

d. a source.

e. a sink.

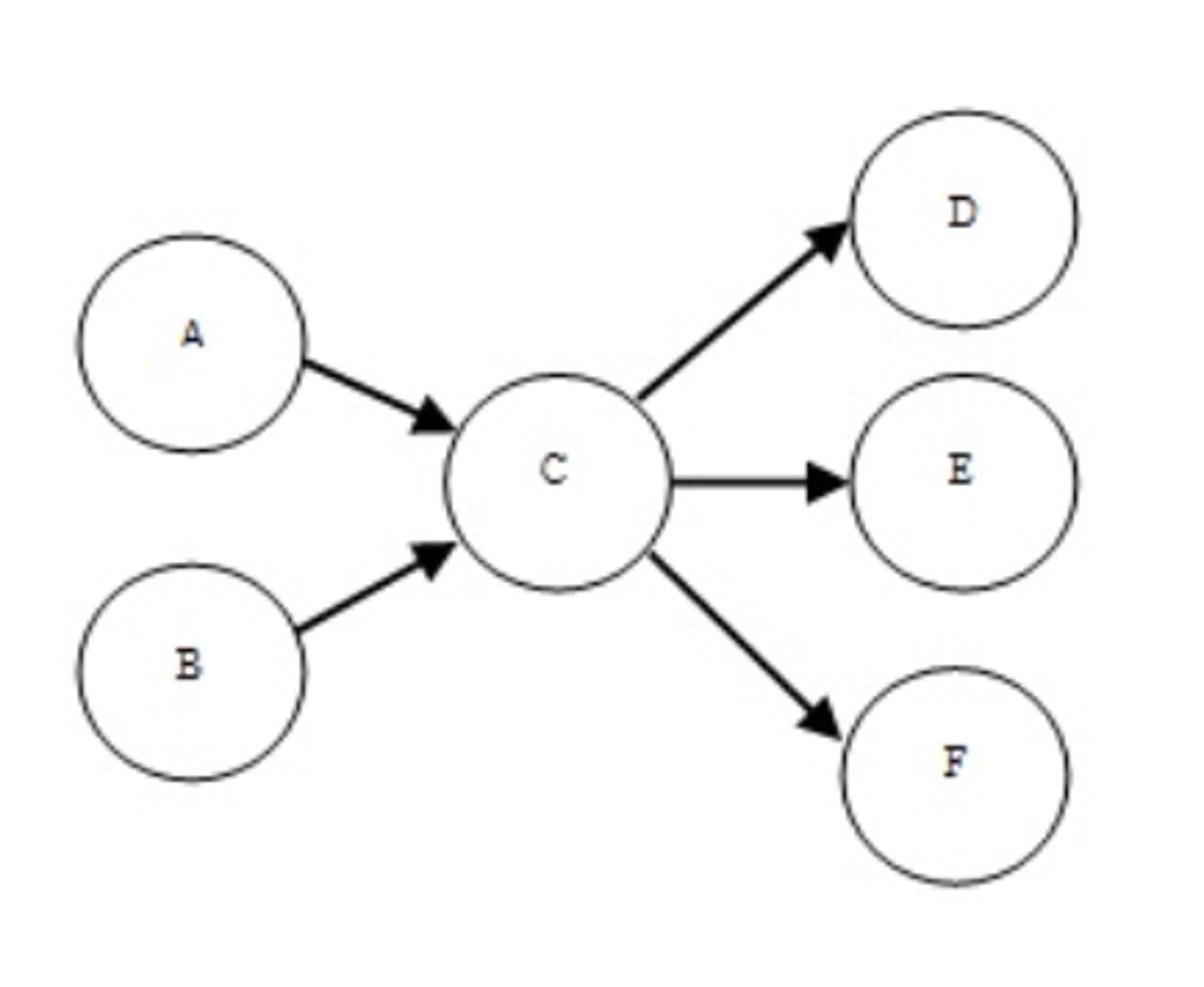
b. 2

In the following network diagram, how many supply nodes are present?

a. 1

b. 2

c. 3

d. 5

e. 6

c. Demand nodes

Which of the following will have negative net flow in a minimum cost flow problem?

a. Supply nodes

b. Transshipment nodes

c. Demand nodes

d. Arc capacities

e. None of the choices is correct.

b. There is an equal number of supply and demand nodes.

Which of the following is not an assumption of a minimum cost flow problem?

a. At least one of the nodes is a supply node.

b. There is an equal number of supply and demand nodes.

c. Flow through an arc is only allowed in the direction indicated by the arrowhead.

d. The cost of the flow through each arc is proportional to the amount of that flow.

e. The objective is either to minimize the total cost or to maximize the total profit.

e. All of the choices are correct.

Which of the following is an example of a transshipment node?

a. Storage facilities

b. Processing facilities

c. Short-term investment options

d. Warehouses

e. All of the choices are correct.

c. There is an equal amount of supply and demand.

For a minimum cost flow problem to have a feasible solution, which of the following must be true?

a. There is the same number of supply nodes and demand nodes.

b. There is only one supply node and one demand node.

c. There is an equal amount of supply and demand.

d. The supply and demand must be integers.

e. The transshipment nodes must be able to absorb flow.

c. Flow can move toward the sink and away from the sink.

Which of the following is not an assumption of a maximum flow problem?

a. All flow through the network originates at one node, called the source.

b. If a node is not the source or the sink then it is a transshipment node.

c. Flow can move toward the sink and away from the sink.

d. The maximum amount of flow through an arc is given by the capacity of the arc.

e. The objective is to maximize the total amount of flow from the source to the sink.

a. Maximize the amount flowing through a network.

What is the objective of a maximum flow problem?

a. Maximize the amount flowing through a network.

b. Maximize the profit of the network.

c. Maximize the routes being used.

d. Maximize the amount produced at the origin.

e. None of the choices is correct.

a. The lines connecting certain pairs of nodes always allow travel in either direction.

Which of the following is not an assumption of a shortest path problem?

a. The lines connecting certain pairs of nodes always allow travel in either direction.

b. Associated with each link or arc is a nonnegative number called its length.

c. A path through the network must be chosen going from the origin to the destination.

d. The objective is to find a shortest path from the origin to the destination.

e. None of the choices is correct.

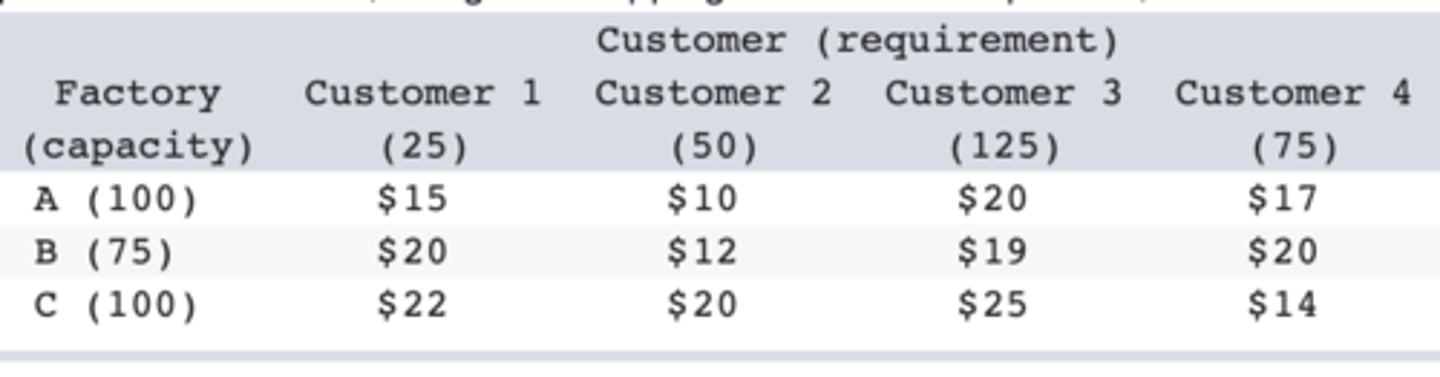
b. Minimum-Cost Flow problem

A manufacturing firm has three plants and wants to find the most efficient means of meeting the requirements of its four customers. The relevant information for the plants and customers, along with shipping costs in dollars per unit, are shown in the table below:

Which type of network optimization problem is used to solve this problem?

a. Maximum-Cost Flow problem

b. Minimum-Cost Flow problem

c. Maximum Flow Problem

d. Minimum Flow Problem

e. Shortest Path Problem

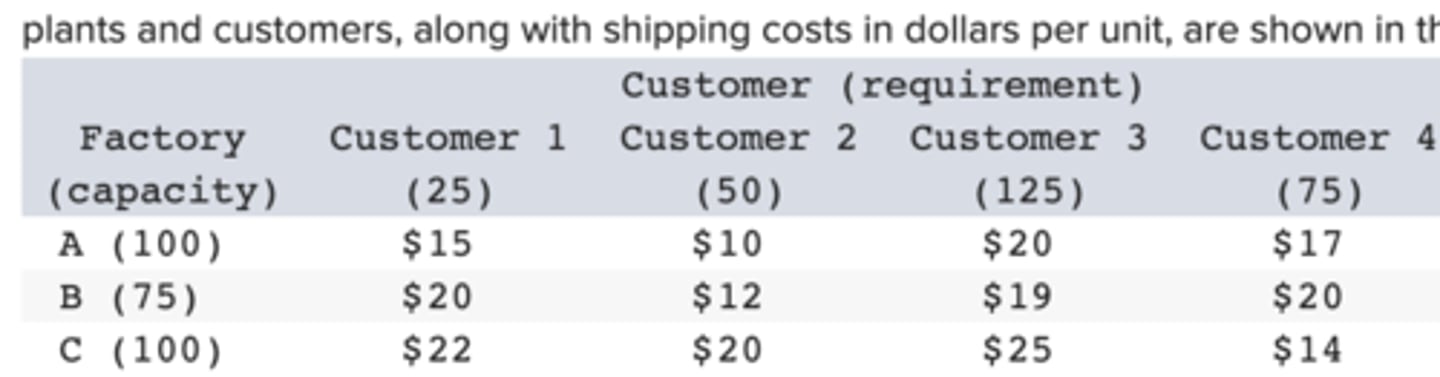
c. 3

A manufacturing firm has three plants and wants to find the most efficient means of meeting the requirements of its four customers. The relevant information for the plants and customers, along with shipping costs in dollars per unit, are shown in the table below:

How many supply nodes are present in this problem?

a. 1

b. 2

c. 3

d. 4

e. 5

d. 4

A manufacturing firm has three plants and wants to find the most efficient means of meeting the requirements of its four customers. The relevant information for the plants and customers, along with shipping costs in dollars per unit, are shown in the table below:

How many demand nodes are present in this problem?

a. 1

b. 2

c. 3

d. 4

e. 5

e. 16

A manufacturing firm has four plants and wants to find the most efficient means of meeting the requirements of its four customers. The relevant information for the plants and customers, along with shipping costs in dollars per unit, are shown in the table below:

How many arcs will the network have?

a. 3

b. 4

c. 7

d. 12

e. 16

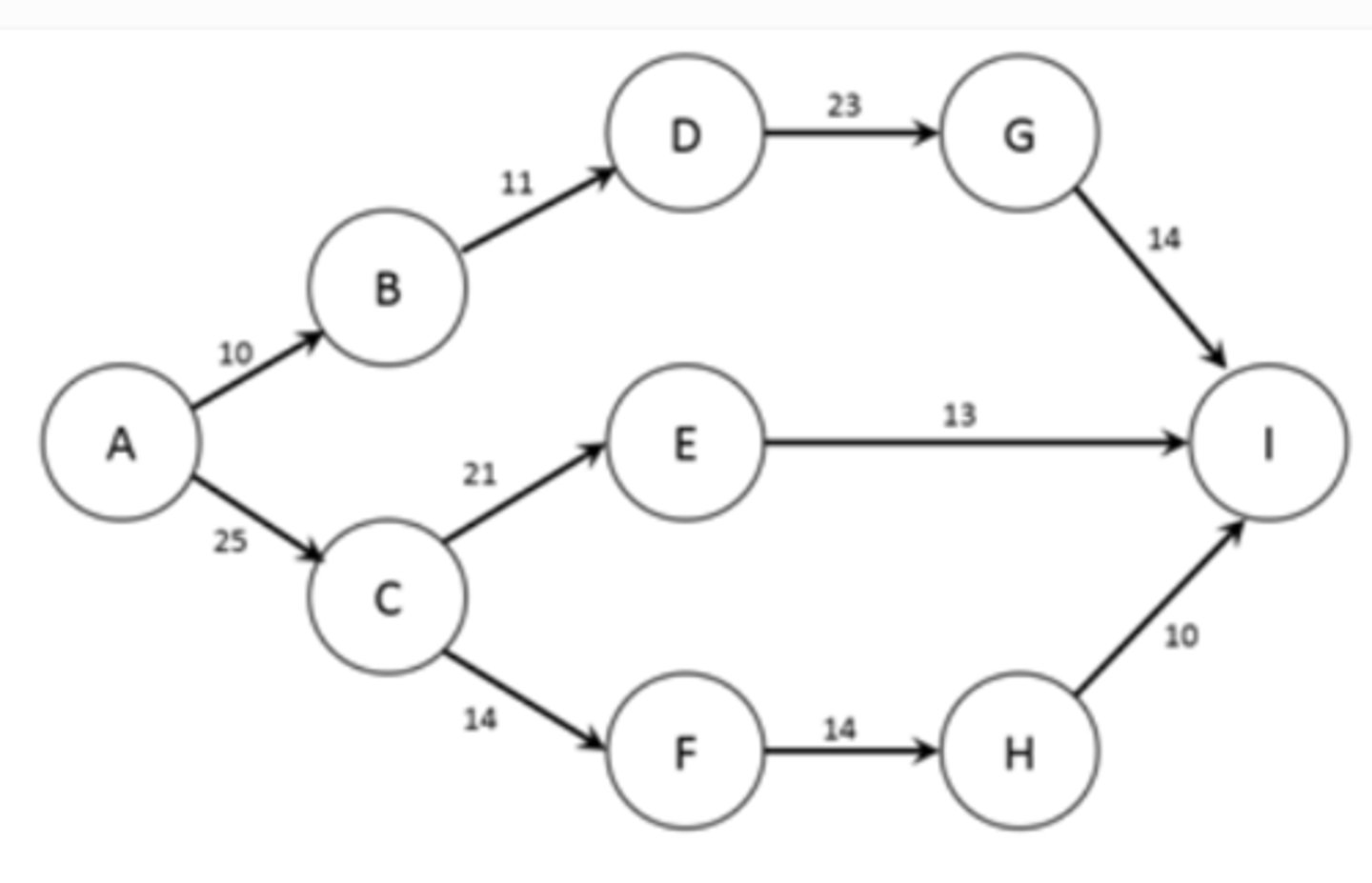
e. Node A is the source, Node I is the sink.

The figure below shows the nodes (A-I) and capacities (labelled on arcs in TB/s) of a computer network. The firm would like to know how much information can flow from node A to node I.

Which nodes are the sink and source for this problem?

a. Node A is the sink, Node I is the source.

b. Node A is the sink, Node B is the source.

c. Node B is the sink, Node I is the source.

d. Node B is the source, Node I is the sink.

e. Node A is the source, Node I is the sink.

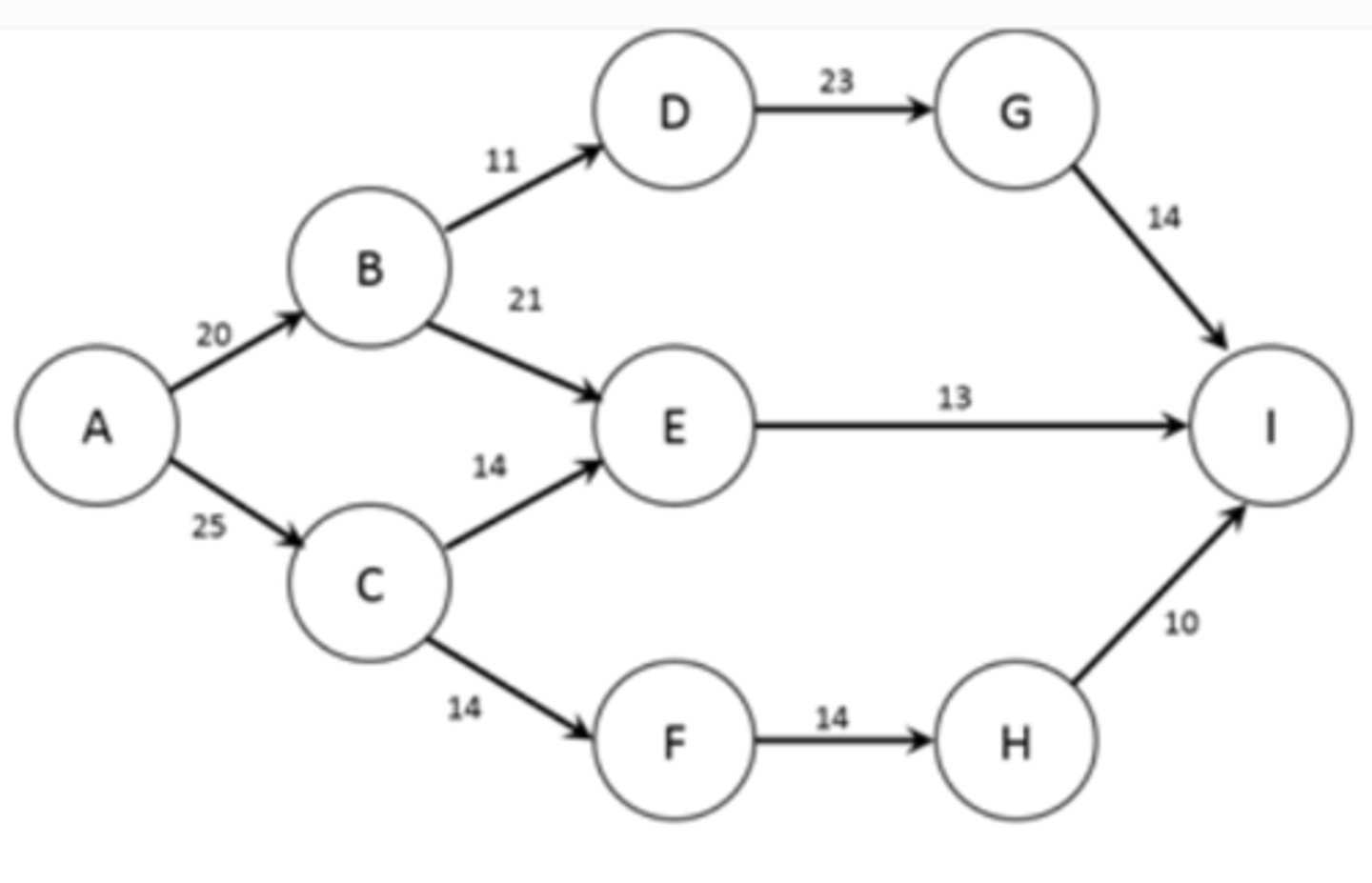
b. 7

The figure below shows the nodes (A-I) and capacities (labelled on arcs in packages/day) of a shipping network. The firm would like to know how many packages per day can flow from node A to node I.

How many transshipment nodes are present in this problem?

a. 6

b. 7

c. 8

d. 1

e. 2

A junction point of a network, shown as a labeled circle

Nodes

A node where the net amount of flow generated (outflow minus inflow) is a fixed positive number.

supply node

A node where the net amount of flow generated (outflow minus inflow) is a fixed negative number, so that flow is absorbed there

demand node

A node where the amount of flow out equals the amount of flow in

Transshipment node

Having the amount of flow out of a node equal the amount of flow into that node.

conservation of flow

A channel through which flow may occur from one node to another, shown as an arrow between the nodes pointing in the direction in which flow is allowed

arc

The maximum amount of flow allowed through the arc.

capacity of an arc

A streamlined version of the simplex method for solving minimum-cost flow problems very efficiently

network simplex method

A special type of minimum-cost flow problem that previously was described in Section 3.5

involves minimizing the cost of shipping something from a number of sources directly to a number of destinations

Transportation problems

A special type of minimum-cost flow problem that previously was described in Section 3.6

involves assigning a group of people to a group of tasks where each person is to per-from a single task

assignment problems

are transportation problems in which a shipment may move through intermediate nodes (transshipment nodes) before reaching a particular destination node

A special type of minimum-cost flow problem where there are no capacity constraints on the arcs.

Transshipment problems

the node at which travel through the network is assumed to end for a shortest path problem

Destination

A fictitious destination introduced into the formulation of a shortest path problem with multiple possible termination points to satisfy the requirement that there be just a single destination

Dummy Destination

a channel through which flow may occur in either direction between a pair of nodes, shown as a line between the nodes

link

the node at which travel through the network is assumed to start for a shortest path problem

origin

the node for a maximum flow problem at which all flow through the network terminates

sink

the node for a maximum flow problem at which all flow through the network originates

Source