Motion

\

Vector VS Scalor

**%%Vector quantities **are physical quantities which can move in a direction and have a magnitude%%, whereas %%scalar quantities %%only have a magnitude but do not move in a direction.

Examples of Vector Quantities

• Velocity
• Acceleration
• Momentum
• Polarization
• Thurst/Drag
• Force
• Weight
• Displacement

Examples of Scalar Quantities

• Temperature
• Mass
• Speed
• Volume
• Time
• Distance
• Density
• Energy/Work

Key Terms & Definitions

Term	Symbol	Definition	Formula	SI Unit	Vector or Scalar?
Displacement	s	Displacement is the distance of a certain direction	n/a	m	Vector
Velocity	v or u	The rate of change in displacement		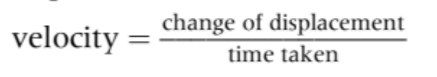	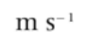Vector
Speed	v or u	The rate of change in distance		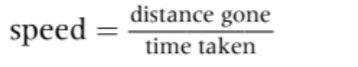	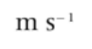Scalar
Acceleration	a	The rate of change in velocity		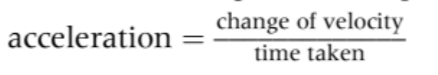	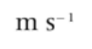Vector

Instantaneous vs Average

• An average value is a value over a certain %%period of time%%
• An instantaneous value is a value is that value at %%one particular time%%

Frames of Reference

• The relative velocity is the %%velocity of an object in regard to another object%%.

  • It is the rate at which one object's relative position changes (rate of change) with respect to another object over time.
  • For example, if a motorcycle is driving at a velocity of120 km/h, and another car is driving at a velocity of 90 km/h, then from the point of view of the car’s passenger, the velocity of the motorcycle relative to the car is 30 km/h

  Explanation

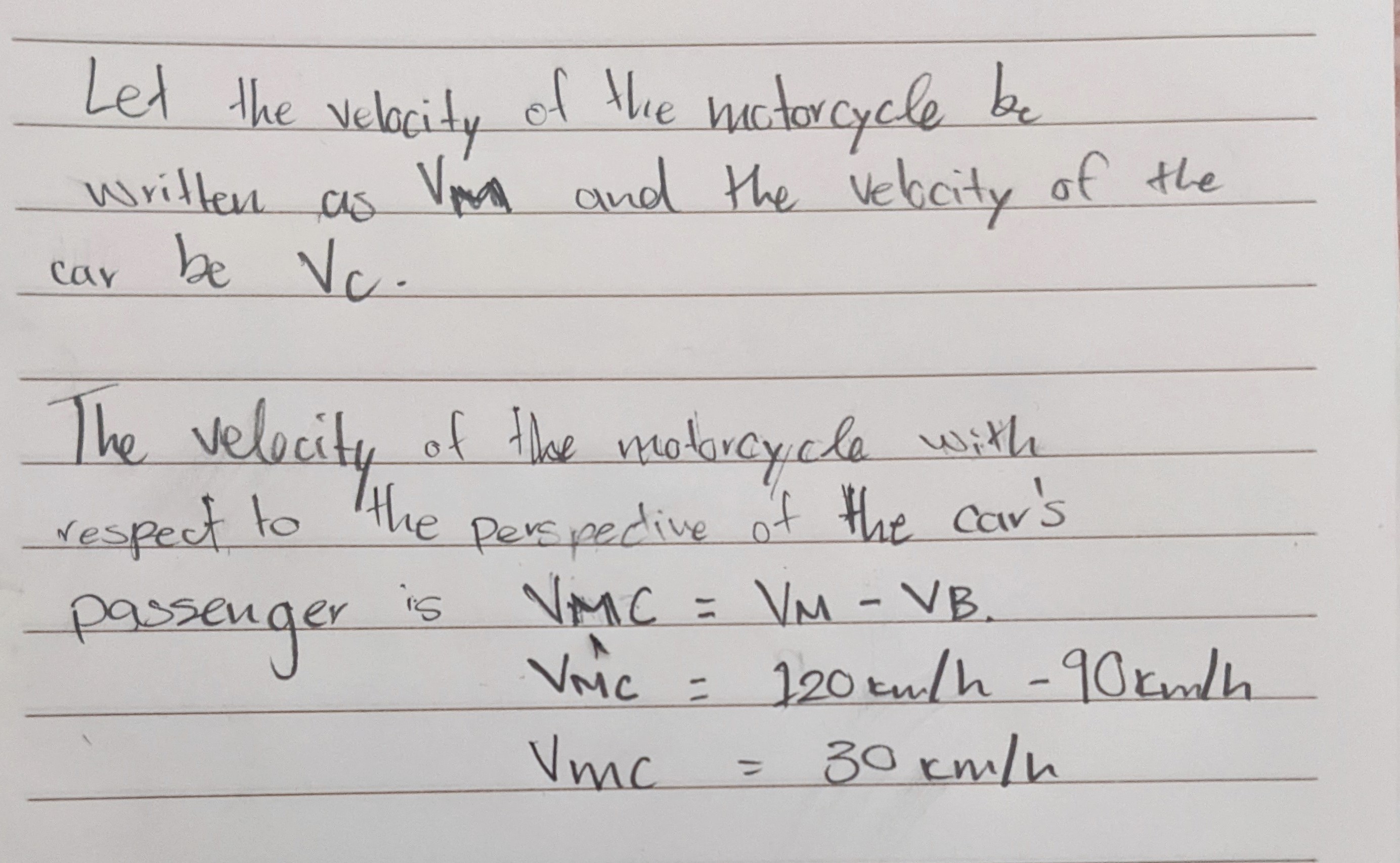  Therefore, the relative velocity of the motorcycle with respect to the car’s passenger is +30km/h.

  In technical terms, we are shifting from one frame of reference to another.

\

Graphical Representation of Motion

There are 3 types of graphs that can provide relevant information on the motion:

• Displacement - Time graphs
• Velocity - Time graphs
• Acceleration - Time graphs

\
There are 2 main ways to determine certain physical quantities within these graphs. The certain physical quantities depend on what is being plotted in the graph.

1. Finding the gradient of the line

WHAT IS A GRADIENT?

• The gradient of the graph is how much it slopes; the larger the gradient, the more vertical it is and the smaller the gradient is, the more horizontal it is.

• Negative gradients have a downward slope

  • To find the gradient, you divide the difference in the y values by the difference in the x values.

  

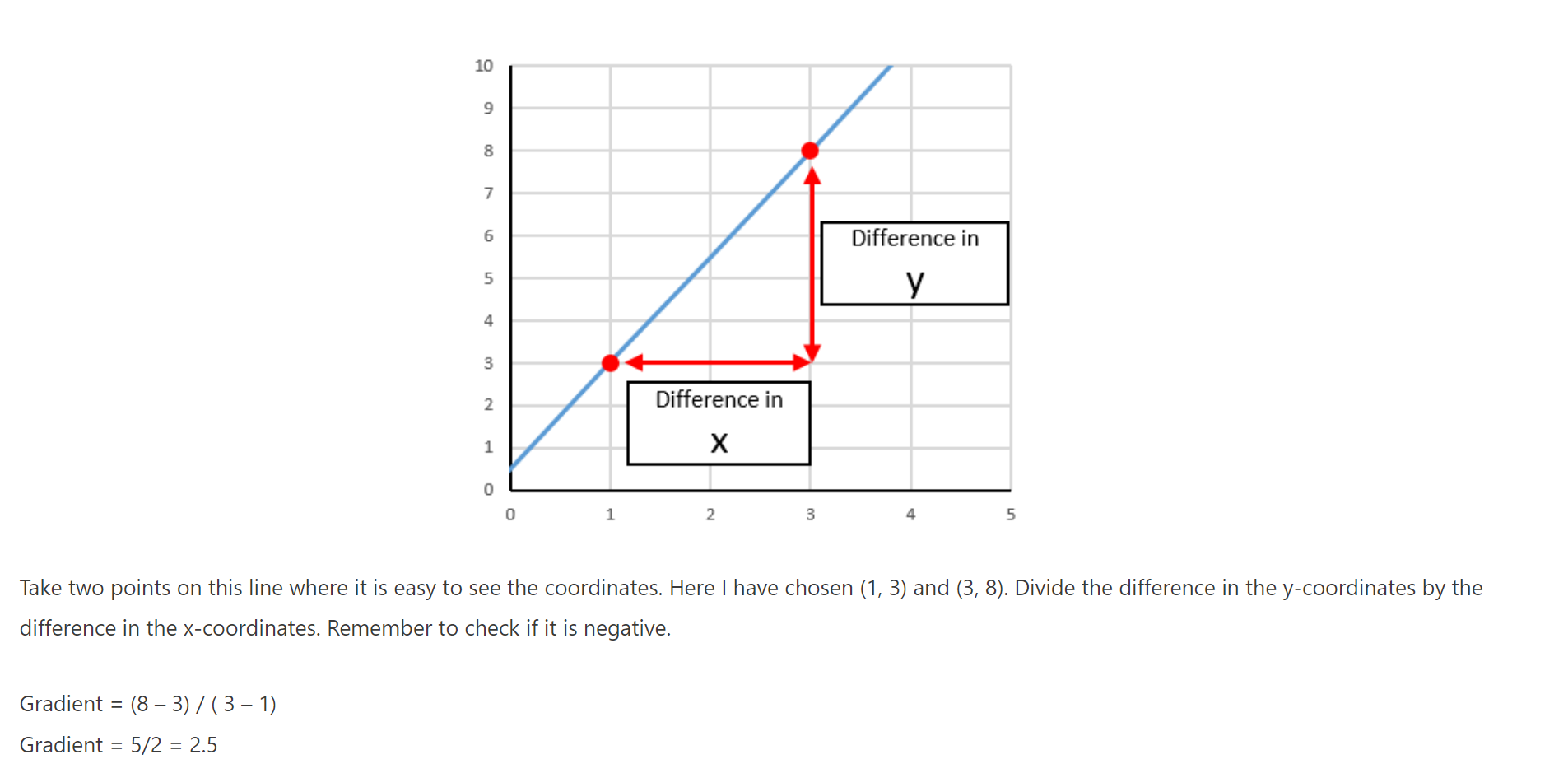
You can find the gradient of:

• a straight-line section of the graph (which finds an average value) or
• the tangent of the graph at a certain point (this finds the instantaneous value)

2. Finding the area under the line

• Consider objects that move in a certain direction
• In complicated graphs, if the object moves up and then down or forward and then backwards, determine the two velocities by choosing which direction is positive.
  • which direction you choose does not matter

\

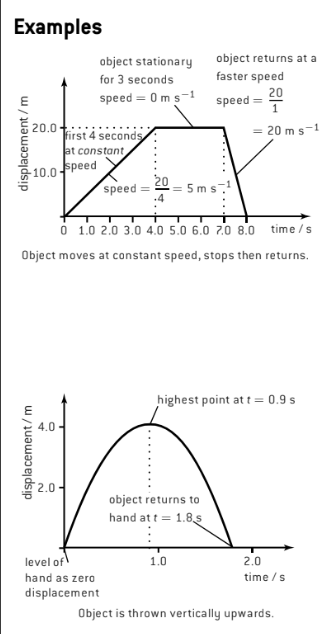
Displacement-Time Graphs

• In displacement-time graphs, the gradient is the velocity
• The area under this type of graph does not portray anything valuable

\

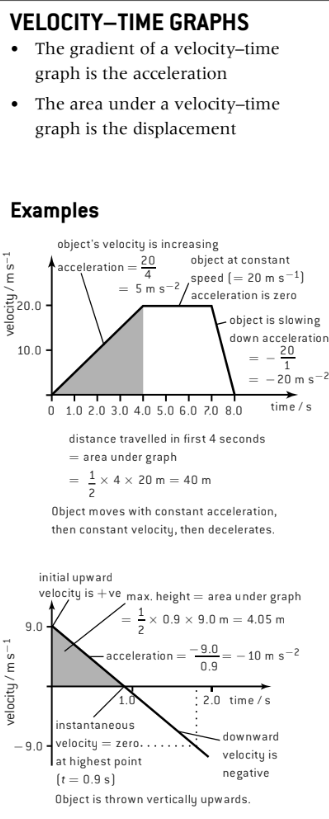
Velocity-Time Graphs

• The gradient in this type of graph displays the acceleration
• The area under the graph displays the **displacement **

\

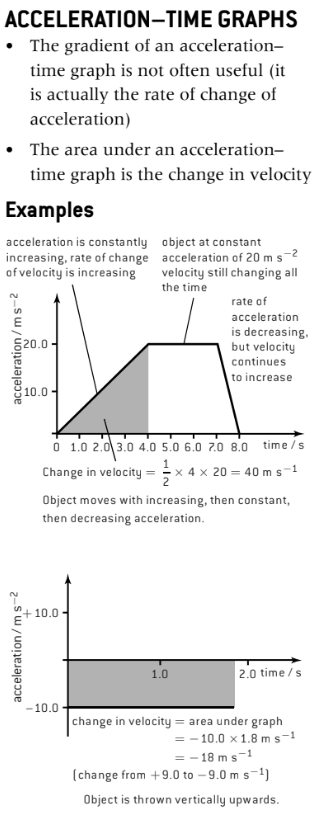
Acceleration-time graphs

• The gradient of this graph is typically useless
  • Depicts the rate of change of acceleration
• The area under the graph showcases velocity

\

\
\
\

Displacement in 2 Dimension

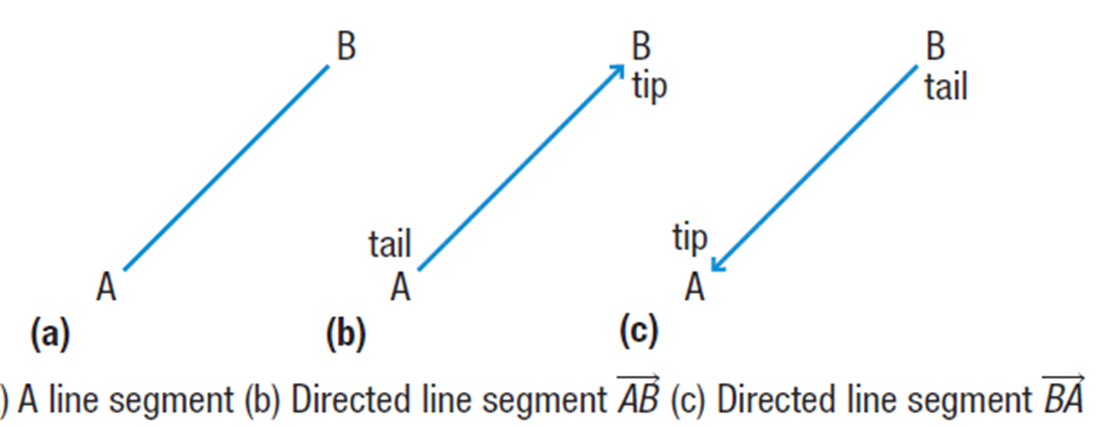
• Vector Scale Diagram: a vector diagram with a specific scale that includes a directed line segment

• Directed line segment: a line which connects to points in a specific direction

  

• There are 3 main components within a vector scale diagram:

  1. Length

     1. how long the vector is

  2. Tip

     1. The point at which the vector starts.

  3. Tail

     1. The point at which the vector ends; it is indicated by an arrow

  

Drawing Vector Diagrams

1. Select a Scale and record it.
2. Select and write down a Reference System (a collection of instructions).
3. Draw the line segment in the proper direction and measure it using the scale.
4. Create an arrowhead at the vector's end.
5. Label the Vector

Vector Directions

• A compass rose can be given to determine the direction of a vector.
• [N 25° E] implies to begin at North (N) and angle your direction arrow 25° towards East (E). This signifies that N is the point of reference.
  • Other approaches to describe this direction are [25° E of N], [25° E from N], [E 65° N], and [65° N of E].
• [25° E of N] implies to turn your direction arrow 25° towards the East, but to begin at the North (N).
• [25° E from N] indicates to turn your direction arrow 25° towards the East, but to begin from the North (N).
• This means that N serves as the reference for both.
• If the number comes first, the reference direction comes last.

\
\
\
\
\
\
\
\
\