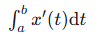chapter 5 Integral basics

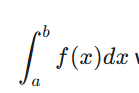
∫ _a^b f(x)dx will find the___

net area

What is the average value of f(x) from x=a to x=b ? (in other words, mean value theorem for integrals?)

1/(b-a) ∫ _a^b f(x)dx

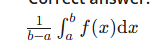
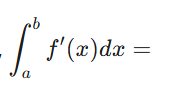
according to fundamental theorem of calculus, ∫ _a^b f’(x)dx = ?

f(b)-f(a)
why?
Total Change = Final Value - Initial Value
Total change = f(b) - f(a) The constant C cancels out. After all, F(x) = f’(x) , so it cancels out leaving f(x) ]^b _a

Area can ___ be negative

NEVER

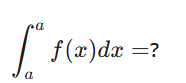
∫ _a^a f(x)dx =

zero

∫ _a^c f(x)dx = ___ + ____ ?

∫ _b ^c f(x)dx +  ∫ _a ^bf(x)dx =

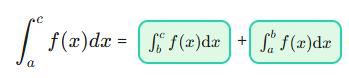
Net area is…

area above minus the area below

∫ _a^b f(x)dx will find

the area between the function above the x=axis and the x-axis minus the area between the function below the x-axis and the x-axis

in other words, positive area (area above x axis) minus negative area (area below x axis)

∫ _a^b f(x)dx = 10, then ∫ _b^a f(x)dx = ?

-10
becomes negative when limits of integrals are switched

d/dx ∫ ₀^x f(t)dt = ?

f(t)
bottom is constant, d/dx cancels out the integral

under vs over estimate: left hand and increasing

underestimate

under vs over estimate: left hand and decreasing

overestimate

right hand, increasing

overestimate

right hand, decreasing

underestimate

midpoint

if concave up, understimate (rectangle below curve)
if concave down, overestimate (rectangle above curve)

trapezoidal rule - over vs under estimate

concave up - overestimate, adds extra area
concave down - underestimate, misses area under curve

delta X ?

(b-a)/n where n is number of subintervals

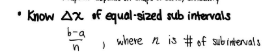
displacement:

change of position, includes negative velocity, distance beginning to end
ex. 2.0 feet, but walk back, -1.0 ft = 1.0 feet total

distance 

includes all distance regardless of velocityies
2.0 ft, but walk back +1.0 = 3.0 feet

x(b) = x(a) + _____ (write as an integral expression)

∫ _a^b x’(t)dt