Conic Sections

Pre-Calculus — 1ˢᵗ Semester, Midterm

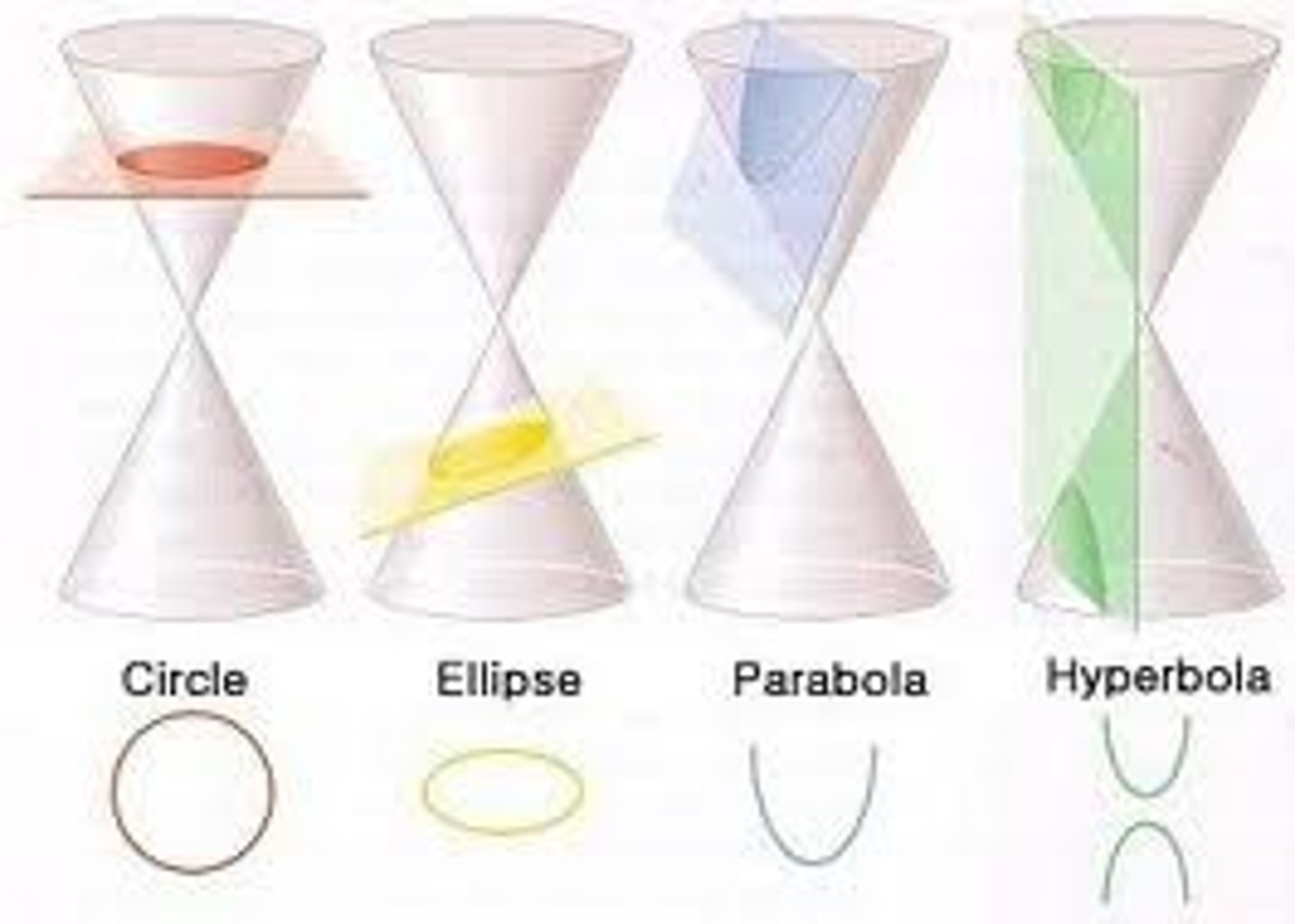
conic section

curve formed by the intersection of a perpendicular plane and a double right circular cone

generator

line lying entirely on the cone

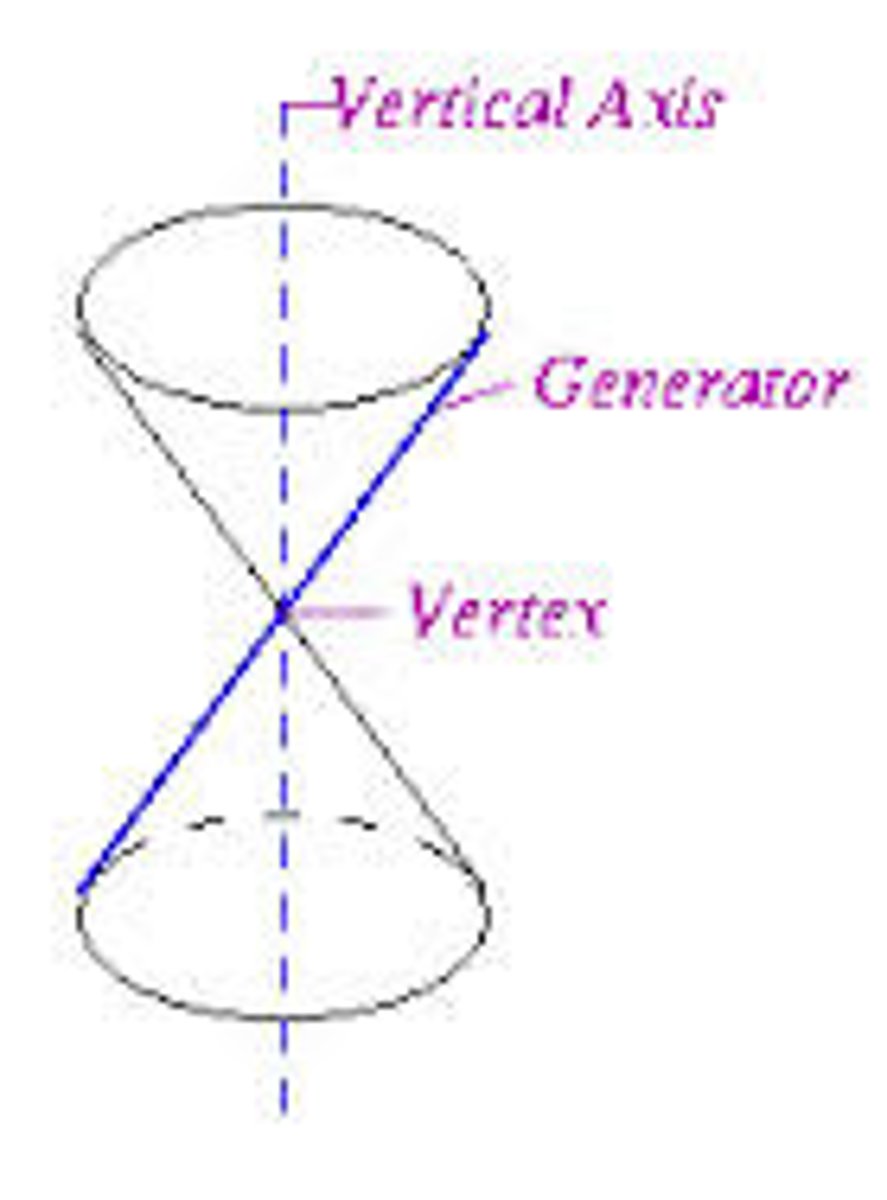
vertex

generators of a cone pass through the intersection of the two parts

parabola

cutting plane is parallel to one and only one generator

ellipse

cutting plane is not parallel to any generator

circle

cutting plane is not parallel to any generator but is perpendicular to the axis

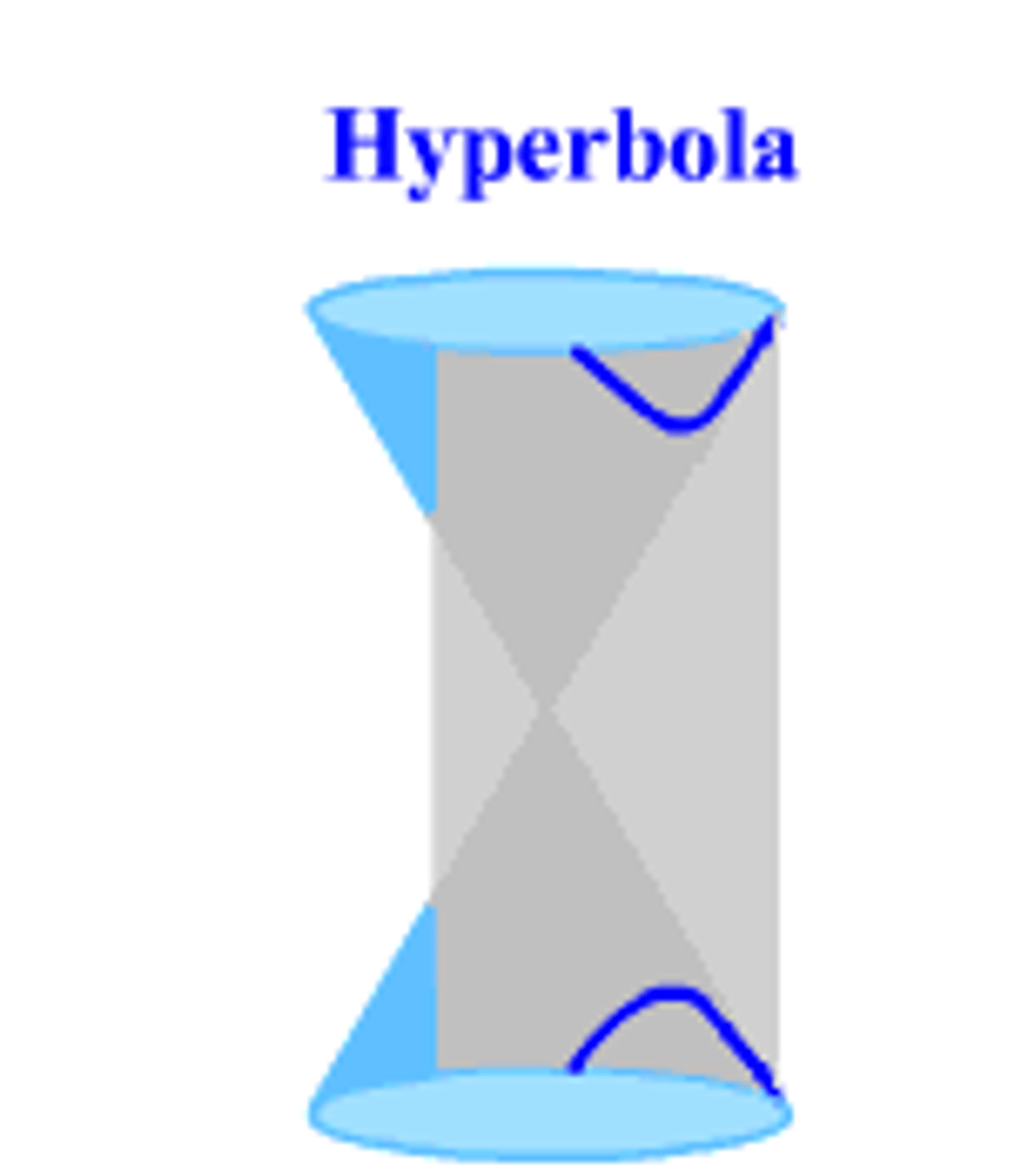
hyperbola

cutting plane is parallel to two generators

non-degenerate conics

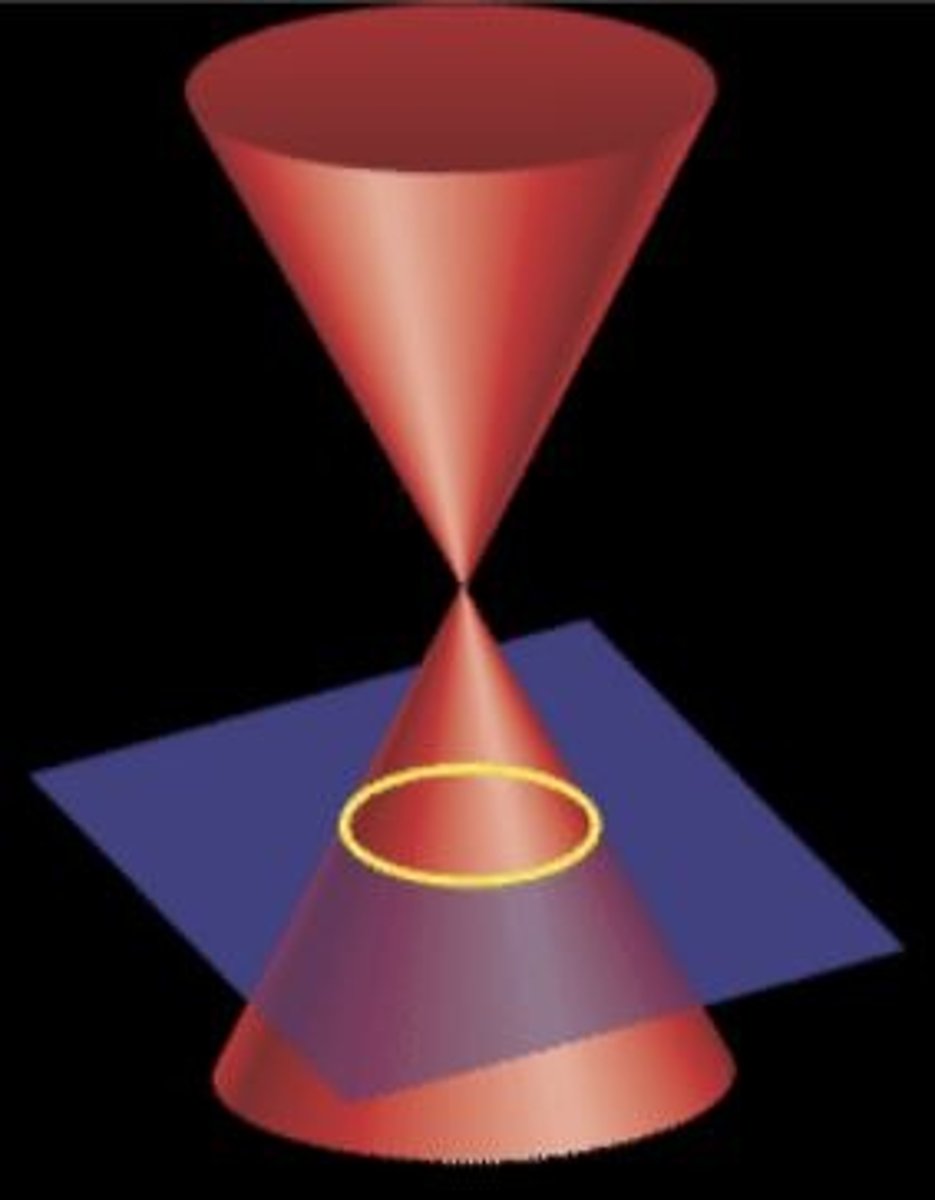
cutting plane does not pass through the vertex of the cone

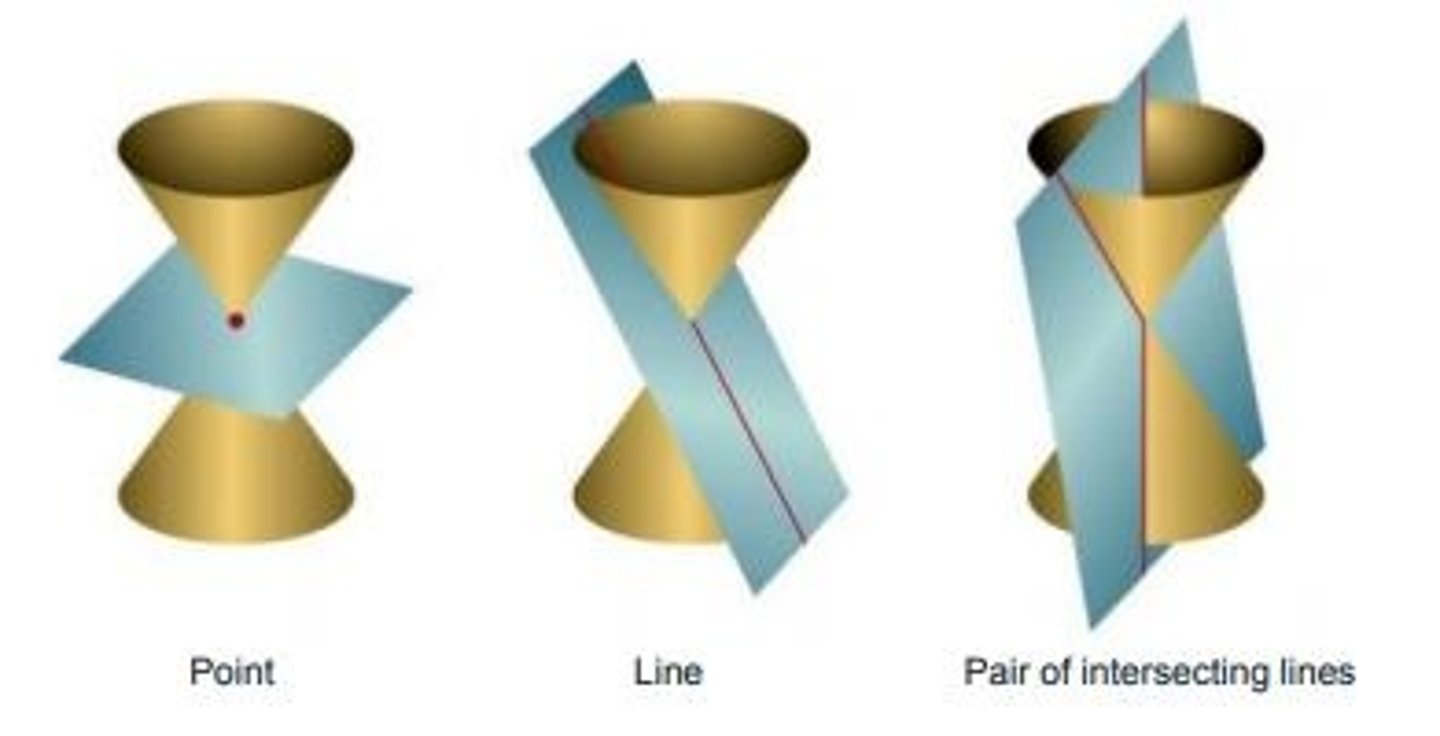
degenerate conics

cutting plane intersects the vertex of a cone

Ax² + Bxy + Cy² + Dx + Ey + F = 0

• where A, B, C, D, E, F are real numbers

general form representing all conic sections depending on its coefficients

B² - 4AC

• where A, B, C are coefficients of x², xy, y²

conic discriminant

B² - 4AC = 0

conic discriminant of a parabola

B² - 4AC > 0

conic discriminant of a hyperbola

B² - 4AC < 0, A = C

conic discriminant of a circle

B² - 4AC < 0, A ≠ C

conic discriminant of an ellipse

x² or y²

conic section of a parabola

• upward = x²

• downward = -x²

• right = y²

• left = -y²

x² and y²

different coefficient

conic section of an ellipse

x² and y²

different sign

conic section of a hyperbola

x² and y²

same sign and coefficient

conic section of a circle