Exam II: Logs and exponential functions

Exponential functions

f(x)= a(b^x)

• b> is greater than 0 but CANNOT be 1

Exponential growth functions

Whenever the base “b” is greater than 1

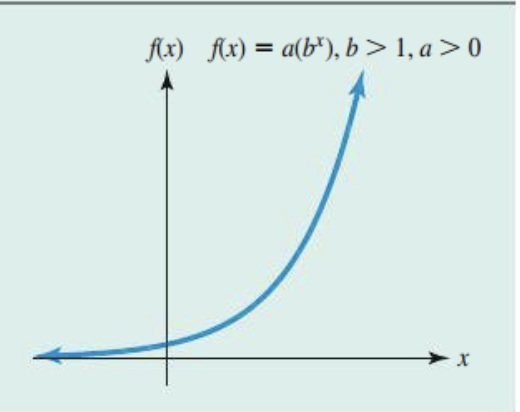
Exponential decay functions

Whenever the base "b" is between 0 and 1

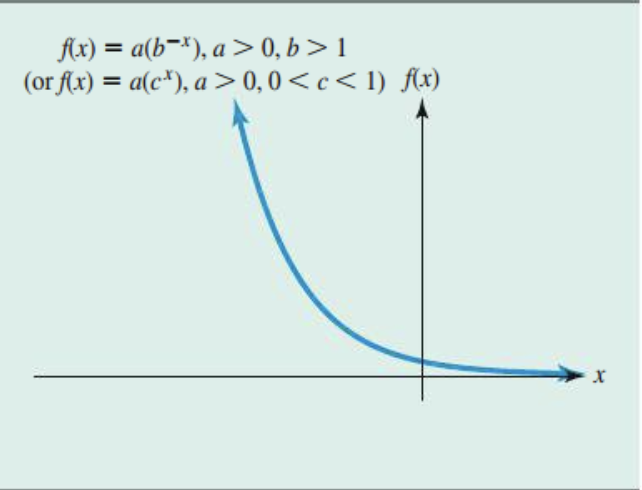
Graphs of Exponential functions

b^x +k

Graph is shifting up

b^x-k

Graph is shifting down

b^x+h

Graph is shifting right

b^x-h

Graph is shifting left

-b^x

Graph reflects across the x-axis

b^-x

Graph reflects across the y-axis

a times b^x

|a| is greater than 1

Graph stretches vertically by a factor of |a|.

a times b^x

|a| is less than 1

Graph compresses vertically by a factor of |a|.

g(x)= b^a times x

|a| is greater than 1

Graph stretches horizontally by a factor of |a|.

g(x)= b^a times x

|a| is less than 1

Graph compresses horizontally by a factor of |a|.

Suppose that inflation is predicted to average 4% per year for each year from 2012-2025. This means that an item costs $10,000 one year will cost $10,000 (1.04) the next year . . . $10,000 (1.04²)

A)Write function that gives the cost of a $10,000 item t years after 2012

$10,000(1.04^t)

Suppose that inflation is predicted to average 4% per year for each year from 2012-2025. This means that an item costs $10,000 one year will cost $10,000 (1.04) the next year . . . $10,000 (1.04²)

C) If an item costs $10,000 in 2012, use the model to predict its costs in 2025

2025-2012= 13

• $10,000(1.04^13)

The inverse of an exponential function

is a logarithmic function that undoes the effect of the exponent.

• y=b^x

• x=b^y (changing y and x values)

• y=logbX

Converting from Exponential to Logarithmic functions:

• 3²=9

Log3(9)=2

• Base of EF= Subscript of LF

• Exponential of EF becomes what we are solving for in Log

• = answer, 9 is after the subscript of Log functions

Converting from Exponential to Logarithmic functions:

• 4^-1= 1/4

Log4(1/4)=-1

• The base of the logarithm corresponds to the base of the exponential function, and the result of the logarithmic function represents the exponent.

5^1=5

Log5(5)=1

x=3^y

Log3(x)=Y

Converting from Log - Exponential functions:

Log2(16)=4

2^4=16

Converting from Log-Exponential:

Log100(0.001)=-4

100^-4=0.001

Converting from Log-Exponential:

Log6(1)=0

6^0=1

Natural Logs

Ln x= Log e(x)

Basic Properties of Log:

1)Logb(B)

=1

Basic Properties of Log:

2) Logb(1)

=0

Basic Properties of Log:

3)Logb (B^x)

= x

Basic Properties of Log

4)b^logb(x)

= x

Basic Properties of Log

5) For positive real numbers M and N, if M=N.

then logb(M) = logb(N).

Use the basic properties of Log

A) log5(5^10)

= 10 , subscript is equaled to the base

Use the basic properties of Log

B) Log4(4)

= 1, because the log of a number to its own base is always 1.

Use the basic properties of Log

C) Log4(1)

= 0, since any log of 1 is equal to 0 regardless of the base.

Use the basic properties of Log

D) Log(10^7)

= 7, because the logarithm of a power is the exponent multiplied by the log of the base. If log doesn’t have a base it’s automatically 10

Use the basic properties of Log

E) Ln e³

= 3, since the natural logarithm of e raised to any power is equal to that power. If Ln doesn’t have a base listed, its automatically e