Mathematics NCEA Lvl 1

Conversion:
converting from fraction to percentage:
vice versa:
converting from percentage to decimal:
vice versa:
Converting from fraction to decimal:

- x100
- Divide by 100
- Divide by 100
- x100
- Calculator Button: S<->D

Practical Conversion:

Practice converting between: fractions, decimals, and percentages (Khan Academy)

State the formulas for:
Increase percentage
Decrease percentage
Percentage of amounts

Increase: Original x (100 + r)%
Decrease: Original x (100 - r)%
POA: % x Original

Formula for calculating a percentage:

B/A x 100

Practical percentages:

Increase percentage
Decrease percentage
Calculating a percentage
Percentage of amounts

What are the two steps to calculating an increase or decrease in percentage changes?

Find the difference
Divide the difference by the original value then x 100

Calculating percentage changes practical:

Pg. 24

GST formulas:
Add:
Take away:
Find GST amount:

x1.15
÷1.15
Find GST exclusive price, then minus it from original amount

GST practical:

Pg. 25 - 26

What is a method for proportional rates?

[Divide the value you want to find by the other value] x Amount

What is a method for inverse rates?

[Divide corresponding value to amount by other value] x Amount

Proportion and Inverse Rates practical:

Pg. 7-8

Formula for A and P of a Rectangle:

p = 2b + 2h
A = bh

Formula for A and P a triangle:

p = a+b+c
A = 1/2bh

Formula for A and P of a circle:

p = 2πr or πd
A = πr squared

Formula for A and P of a parallelogram:

p = 2a + 2b
A = bh

Formula for A and P of a trapezium:

p = a+b+c+d
A = [base x top/2] xh

Area and Perimeter practice:

Pg: 122

What are compound shapes made up of?

Two or more other simple shapes

Practical: Compound shapes and shapes with holes

Pg 123 - 124

State the formula for the volume of a cuboid:

height x width x depth (hwd)

State the formula for the volume of Prisms:

Area of base x depth

State the formula for the volume of a cylinder:

Area of base x depth (πr^2 x d)

State the formula for the volume of a pyramid:

1/3 x (base area) x height

State the formula for the volume of a Cone:

1/3 x (base area) x height

State the formula for the volume of a Sphere:

4/3 x πr^3

Practical for Volume:

Pg 130 - 132

State the formula for the surface area of a cylinder:

Area of curved side + 2(area of end)

State the formula for the surface area of a triangular prism:

2(area side) + area base + 2(triangular end)

State the formula for the surface area of a Pyramid:

Base area + 4(area side)

State the formula for the surface area of a sphere:

4πr^2

State the formula for the surface area of a Cone:

πr^2 + πr x L

Surface area of 3D shapes practical:

Pg: 127 - 128

Practical compound shapes: surface area and volume

Pg: 133 - 135

State the formula for the Pythagoras Theorem

a^2 + b^2 = c^2

What is the hypotenuse of the triangle in the Pythagoras Theorem?
What is it represented by in the Pythagoras Theorem?

• opposite to right angle and longest side of triangle

• 'c’

Pythagoras Theorem practice:

Pg. 97

Multistep and 2D practical problems Pythagoras Theorem practical:

Pg 98 - 100

Tip for 3D problems Pythagoras Theorem: Draw 2D __ that contains the __ or __ of the triangle. Only draw the __ that the __ crosses over or touches.

Draw 2D -shapes- that contains the -length- or -angle- of the triangle. Only draw the -shapes- that the -triangle- crosses over or touches.

3D problems practical Pythagoras Theorem:

Pg 101 - 102

What is the turning point (round edge) of a parabola called?

The vertex

What is the vertex of a parabola?

The very middle point of a parabola. (The max or min point.)

Plotting quadratic equations using parabola practical:

Pg: 80-81

Parabola Vertex:
What does a hill shape mean?
What does a pit shape mean?

• Vertex = max point

• Vertex = Min point

Optimizing by graphing quadratics:
What should you give the value 'x'?
What relationship between two variables do you plot?
What do you do when the value 'y' or the area values repeat?
What is the vertex of a parabola with two of the same vertex values?

• A series of values

• Plot relationship between x and y (variable that needs to be optimized - the area)

• Do not continue the table as you will be repeating values

• If two 'y' or area values are the same, create a new series of values and plot the relationship between x and y

Optimizing by graphing quadratics practical:

Pg: 83-86

What defines a quadratic expression?
What does a quadratic expression look like when graphed?

• An expression with the highest power of a variable being 2

• A parabola

What are the two possible steps to expanding quadratic expressions?

1. Use FOIL: First, Outer, Inner, Last

2. Combine Like terms to simplify where applicable

What is the usual form of quadratic expressions when expanding?

x^2 term, x term, constant

Expanding quadratic expressions practical

Pg 50 - 51

What are the three types of factorizing quadratic expressions?

1. where the coefficient of x^2 is 1

2. where the coefficient of x^2 is not 1 but a common factor is present

3. where the coefficient of x^2 is not 1 and a common factor is not present

What are the 3 steps to factorizing quadratic expressions where the coefficient of x^2 is 1:

1. List all factors of constant (the whole number)

2. Choose the pair of factors from the constant that could add or subtract to give the coefficient of x (the number next to x)

3. Input the factors into the formula of either: (x_a) (x_b) or x(x_a)

What is the formula for an example with a representation of: a - bx^2? (For example: 9 - 4x^2).
Steps to factorize this type 1 quadratic equation: (1) Find the __ value of each equation component. (2) Factorize the __ __ into a bracket. (3) Put into formula: __ __.

(a+b) (a-b) = a^2 + 0 - b^2 = a^2 - b^2
(1) Find the squared value of each equation component. (2) Factorize the x term into a bracket. (3) Put into formula: (a+b) (a-b)

factorizing quadratic expressions where the coefficient of x^2 is 1 practical

Pg 52 - 53

What are the three steps to solving a quadratic expression when the coefficient of x^2 is not 1 but a common factor is present? E.g. 2x^2 - 6x - 8

1. Find the CF that divides into the coefficients and constant, then place before the brackets (further left side).

2. List the corresponding factors of the CF that divide into the coefficients and constant and place them in the brackets.

3. Factorize contents inside brackets, leaving CF outside of brackets on far left.

Solving a quadratic expression when the coefficient of x^2 is not 1 but a common factor is present practical

Pg. 54

What are the 6 steps to solving a quadratic expression when the coefficient of x^2 is not 1 and there is no common factor is present? E.g. 2x^2 + 3x - 20

1) Multiply coefficient of x^2 by constant
2) list factors of the previous step's result
3) Choose the factors pair that adds to the coefficient of x
4) Input the factors pair as a replacement of the previous 'x term' to make two new 'x terms'
5) Half the new quadratic expression into two pairs - first pair of two terms and second pair of two terms. Then factorize the two pairs separately (bracket components of CF should be the same)
6) Factorize the new quadratic expression by putting the bracket contents of the CF on the left side and the remaining values as the second bracket components on the right side

Solving a quadratic expression when the coefficient of x^2 is not 1 and there is no common factor is present practical

Pg. 55 - 56

What is substitution?

replacing variables with numbers

Substitution practical

Pg. 28

What is the goal of rearranging expressions?

To isolate the subject (e.g. isolate V in: gh = V x 9e)

Hints for the rearrangement of expressions where the subject appears once:
Put all __ containing the __ on the __.
Get rid of fractions by __ by the __ __ __ of the denominators.
Get rid of square roots by __ it on one side then __ __ sides.
Use normal __ __.

Put all terms containing the subject on the left.
Get rid of fractions by multiplying by the lowest common multiple of the denominators.
Get rid of square roots by isolating it on one side then squaring both sides.
Use normal solving rules.

Rearrangement of expression where the subject appears once practical

Pg. 96 - 97

When multiplying powers...
Formula:

add the powers

Multiplying powers practical

pg. 15

When dividing powers...
Formula:

subtract powers

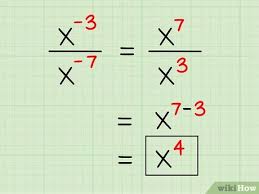
Dividing powers practical

pg. 16

When finding powers of powers...
Formula:

multiply powers

Powers of Powers practical

pg. 17

Powers varied questions practical

pg. 18

Fractional powers & Roots: Complete the formulas below on a paper
a^1/m = ...
a^m/n = ...

^m√a
^n√a^m OR (^n√a)^m

Fractional powers and roots:
What is the index form in simple terms?
What is always present in a surd form?

- fraction form
- a square root symbol

Reminders for fractional powers and roots:
The denominator of an index form becomes the...in the surd form and vice versa.
The numerator of an index form belongs to the...in the surd form and vice versa.

- exponent of the square root symbol
- value inside the square root

Fractional powers and roots practical

pg. 20

What are negative powers?
How do you find negative powers?

• reciprocal of positive powers

• turn the fraction upside down

negative powers practical

pg. 21

Equations with powers steps: (1) Rewrite the expression with the __ __ possible. (2) There must be __ expression using the __ __ on __ side of the equal sign. (3) Use power laws to __ the expression. (4) Since the base numbers are the __, the __ exponents become __.

(1) Rewrite the expression with the smallest base possible. (2) There must be one expression using the same base on each side of the equal sign. (3) Use power laws to simplify the expression. (4) Since the base numbers are the same, the power exponents become equal.

Equations with powers practical

pg. 22

What are the three types of forming and solving linear equations:

1. Given relationships between angles, lengths, areas and volumes.

2. given two pairs of values (points on a graph) that satisfy the equation.

3. Given that the equations represent parallel or perpendicular lines

Tips for forming and solving linear equations when given relationships between angles, lengths, areas and volumes: (1) Define the variable using the first __ of the __ whose value needs to be __. E.g. Area = __. (2) If finding __ values, it is easiest to select the __ value as the __.

(1) Define the variable using the first letter of the word whose value needs to be found. E.g. Area = a. (2) If finding several values, it is easiest to select the smaller value as the variable.

Forming and solving linear equations when given relationships between angles, lengths, areas and volumes practical

pg. 31 - 32

Forming and solving linear equations when given two pairs of values (points on a graph) that satisfy the equation:
Write the formula to calculate the gradient:
Write the formula that satisfies the equation given:

• m = rise/run = y2-y1/x2-x1

• y1 = m(x-x1)

Forming and solving linear equations when given two pairs of values (points on a graph) that satisfy the equation steps: (1) Name the __. (2) Calculate the __ using the formula __. (3) Calculate the __ using the formula __.

(1) Name the coordinates. (2) Calculate the gradient using the formula m = y2-y1/x2-x1. (3) Calculate the equation using the formula y-y1 = m(x-x1).

Forming and solving linear equations when given two pairs of values (points on a graph) that satisfy the equation practical

pg 33-34

In relation to a graph, what do parallel lines have?
Write the equation that represents this relationship:

• equal gradients

• m1 = m2

what type of lines on a graph have right angles to each other?

Perpendicular lines

The gradients of perpendicular lines are...
Write the equation of the relationship above:

• negative reciprocals of each other

• m1 x m2 = -1

Steps/pointers when dealing with parallel lines: (1) Name the __. (2) __ the given expression for a line if needed. (3) The coefficient of 'x' is the __ (m). (4) Use the formula: __

(1) Name the coordinates. (2) Simplify the given expression for a line if needed. (3) The coefficient of 'x' is the gradient (m). (4) Use the formula: y-y1 = m(x-x1)

Steps/hints when dealing with perpendicular lines: (1) Name the . (2) __ the given line equation if needed. (3) Identify m1: m1 = coefficient of '' OR __ __ containing 'x'. (4) Use formula "__" to find m2. (5) Use formula: __, where 'm' is the value of __.

(1) Name the coordinates. (2) Simplify the given line equation if needed. (3) Identify m1: m1 = coefficient of 'x' OR index form containing 'x'. (4) Use formula "-1/m1" to find m2. (5) Use formula: y-y1 = m(x-x1), where 'm' is the value of m2

Forming and Solving linear equations where it is given that the equations represent parallel or perpendicular lines practical

pg. 35-36

Write the equation for a straight line:

y = mx + c

"What does the c represent in y = mx + c?

The y intercept on the y axis

Write the equation to find a straight line:

y-y1 = m(x-x1)

What are simultaneous equations?

solving multiple equations at the same time

What are two methods of simultaneous equations?

Substitution and elimination

Tips for substitution of simultaneous equations: (1) substitute the "" or "" value into the other __. (2) __ each equation and __ what is being done at each step. E.g., "Substitute 1 __ 2" or "substitute for __ in 1". (3) Check answers by __ the final answers into the __ equations. (4) Put the final values into __ __. E.g. (4,5).

(1) substitute the "x..." or "y..." value into the other equation. (2) Number each equation and explain what is being done at each step. E.g., "Substitute 1 into 2" or "substitute for y in 1". (3) Check answers by substituting the final answers into the original equations. (4) Put the final values into coordinate form. E.g. (4,5).

Substitution for simultaneous equations practical

pg. 43-44

How can you identify whether to use elimination for simultaneous equations?

When two equations have the same structure.
E.g. x terms, y terms, constants, and equal signs in same place: 5x + y = 7 and 2x + 3y = 12

How do you solve a simultaneous equation using elimination?

Multiply either one or both equations present by a constant or constants to make either the 'x' or 'y' terms the same size but with opposite signs. E.g. +4y and -4y = they are the same size (4y) but with opposite signs (+ and -)

Elimination to solve simultaneous equations hints: (1) Add the __ after solving them to produce an equation with only __ variable. (2) __ each equation and say what is being done at each step. E.g. "Multiply 1 by -4" or "Add 2 and 3".

(1) Add the equations after solving them to produce an equation with only one variable. (2) number each equation and say what is being done at each step. E.g. "Multiply 1 by -4" or "Add 2 and 3".