LSU ISDS 2000 Test 1 Study Guide: David Whitchurch

Statistics

a branch of applied mathematics which involves the collection, organization, analysis, interpretation, and presentation of data

The study of statistics consists of two branches

descriptive statistics and inferential statistics

Population

includes ALL observations for which conclusions are to be made. In many situations, it is either impossible or not practical to collect information from this, so the analyst will take a sample instead

Sample

a subset of the population

descriptive statistics

methods used to summarize your data so that you can explain the important characteristics

descriptive statistics examples

Examples include creating pie charts, histograms, or line graphs, calculating the mean, median, mode of home values by geographic region, reporting crime rates by types of crimes, unemployment rate over time, DJIA, the number of freshman entering LSU this past fall by academic major, etc.

inferential statistics

methods that use data from a sample to make conclusions and decisions about the population

inferential statistics example

According to the Centers for Disease Control, 'people who smoke cigarettes are 15 to 30 times more likely to get lung cancer or die from lung cancer than people who do not smoke.'

Parameter

a summary measure that describes a characteristic of an entire population

Statistic

a summary measure that describes a characteristic of a sample

Cross-sectional data

contains measurements of observations at one point in time (e.g., results from a survey taken on January 1, 2024)

Time series data

contains measurements of observations over multiple periods of time (e.g., results from a survey taken every year from 2019- 2024)

Structured data

data stored in spreadsheets or relational databases and have a pre-defined row-column format

Unstructured data

has no structure and does not follow a pre-defined format.

Examples of unstructured data include

email messages, blogs, customer comments, medical imaging, photos, videos, music clips

Big data

a collection of large, complex data sets, including structured and unstructured data, which cannot be analyzed using traditional database methods and tools

Variable

the characteristic of an observation that is apt to change or vary

Data

the values associated with each variable

Categorical Variables (also known as Qualitative variables)

have values that facilitate placing an observation into a specific category

Categorical Variables examples

Examples: gender, political affiliation, city of birth, whether a product is defective (yes or no), product quality (superior, good, fair, poor)

Numerical Variables (also known as Quantitative Variables)

have values that represent quantities and are the result of a measuring process

Numerical Variables Examples

salary, revenue, expenses, return on investment, amount spent, number of items purchased, salary, return on investment, GPA, number of children

Subtypes of numerical variables include

Discrete and Continuous

Discrete

result of counting

continous

measurements can take on infinitely many values within an interval

Variables are also identified by their

scales or levels of measure

The four scales of measures

Nominal, Ordinal, Interval, Ratio

a categorical variable has a nominal scale if

its values allow us only to categorize observations into mutually exclusive groups

Nominal examples

gender, academic major, race, state of birth, commute to campus or not, etc.

a categorical variable has an ordinal scale if

its values allow us to both categorize and rank the observations according to some quantity or trait

Ordinal examples

grade in your class (A, B, C, D, or F), customer rating when purchasing a product (Excellent, Good, Fair, Poor), Skip Class (Never, Very Rarely, Somewhat Often, Very Often), Salary (Low, Middle, High), etc

a numeric variable has an interval scale if

its values allow us to both categorize and rank observations, and, in addition, the differences in values have a consistent meaning

Interval examples

Temperature in Fahrenheit or Celsius. Ninety degrees is hotter than 80 degrees, and a 10-degree difference has the same meaning across its entire range. (i.e.: equivalent to the difference between 30 degrees and 20 degrees)

a numeric variable has a ratio scale if

it has all characteristics of an interval-scaled variable and has a true zero point

Ratio examples

example: salary

Variables having nominal and ordinal scales of measurement are always

categorical

Variables having interval and ratio scales are always

numerical

Frequency Table

a tabular summary of a data showing the frequency (or percent) of items in each of the distinct categories represented by the categorical.

Bar Graph

a graphical display of data where each category is depicted by a unique bar with the height of the bar representing the frequency, or proportion, of observations in that category

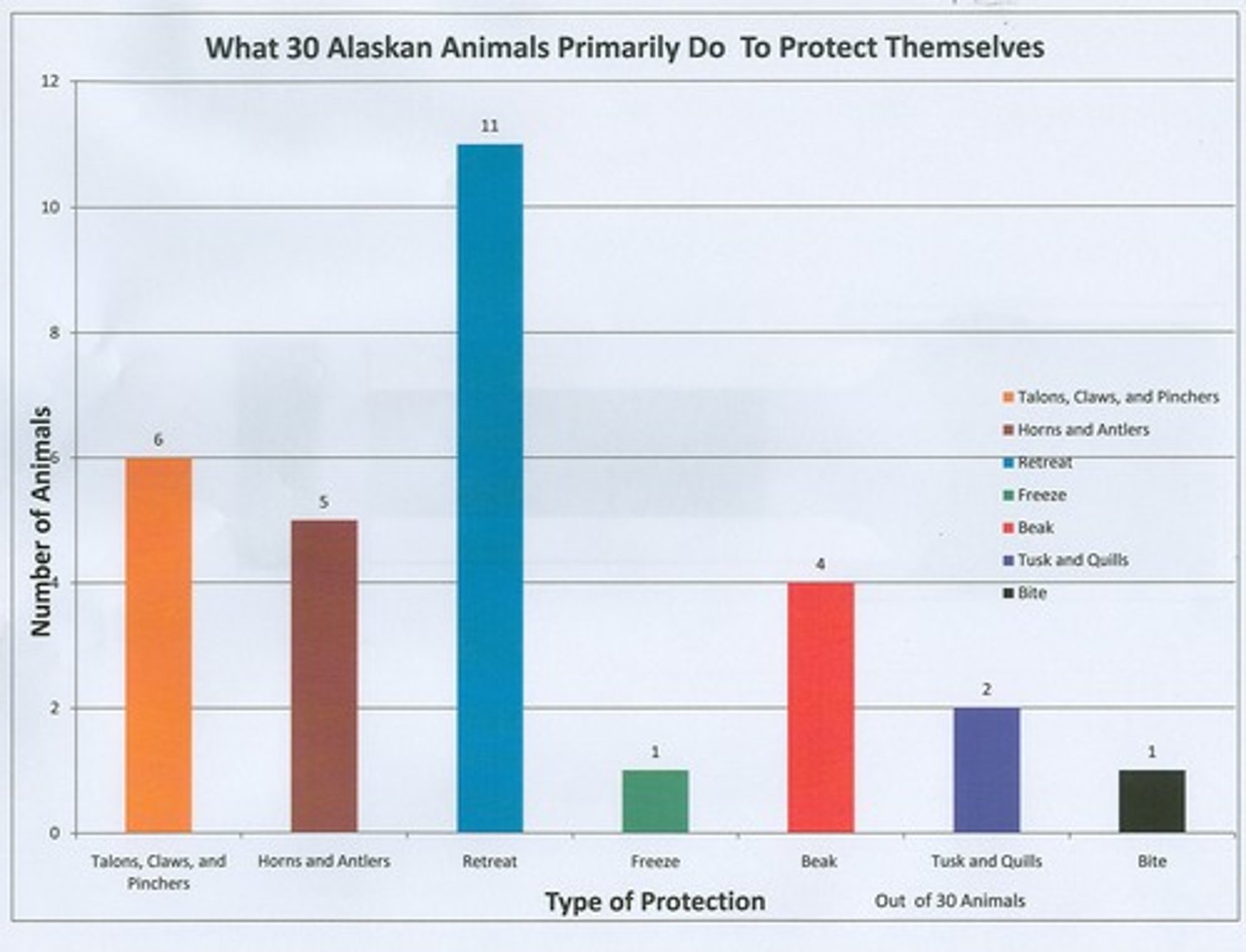
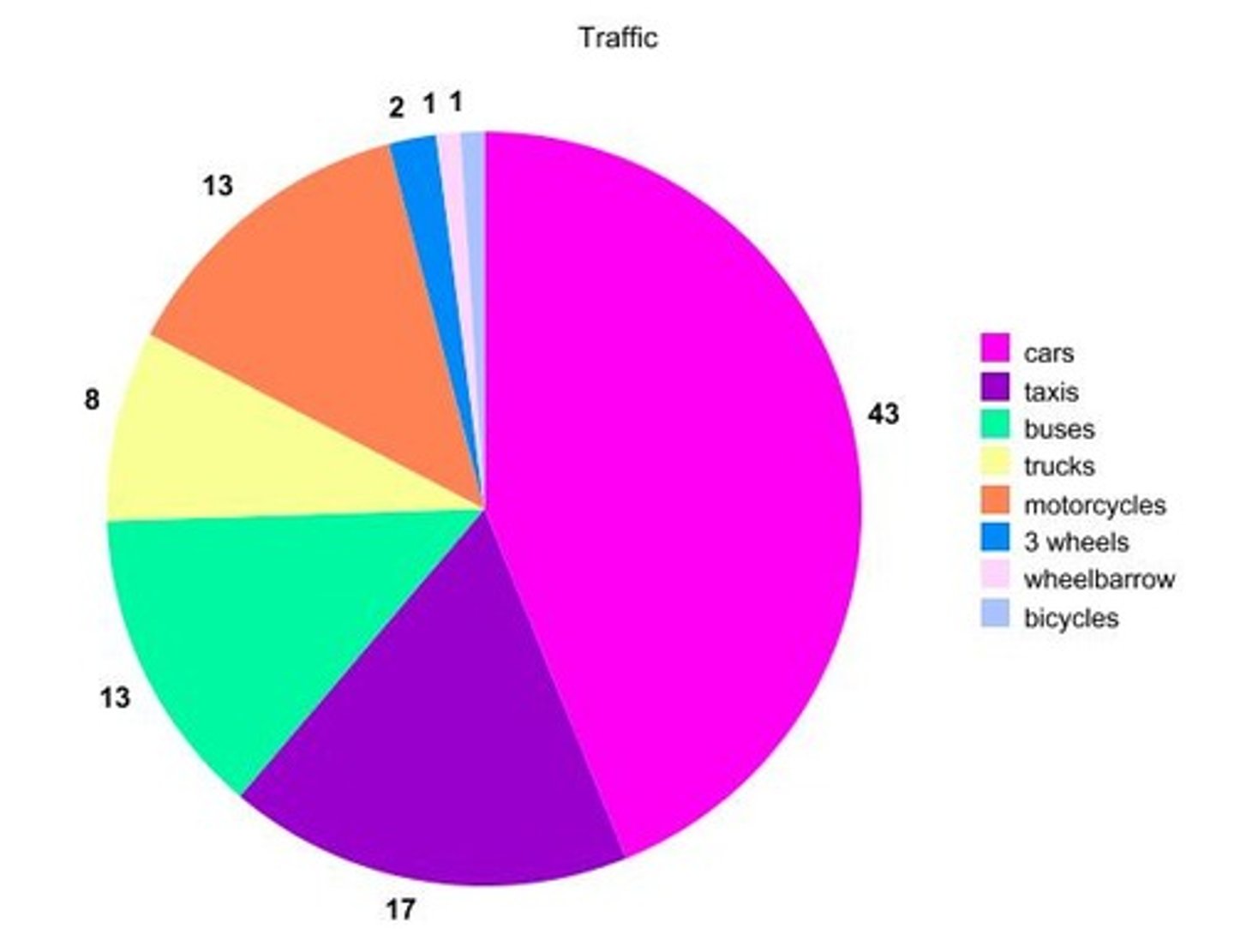
Pie Chart

a graphical display of data where each category is depicted by a unique slice of the pie, in degrees, which represents the frequency, or proportion,

of observations in that category

The number of categories usually ranges from ___________, depending upon the data

set size

5 to 20

Larger data sets require _________ categories, whereas smaller data sets require ________ categories; # of classes = # of bars in the histogram.

more, less

The categories are _____________ so that they do not overlap, and each observation is placed in only one category

mutually exclusive

The categories are exhaustive in that they all cover the....

entire range of data

The endpoints and width of the categories are.....

(note that the width is the same across all categories)

easy to interpret

Steps to Construct a Frequency Table for a Numerical Variable

1. Determine the range of the data from an ordered array

2. Specify the number of categories and calculate the WIDTH of each category

3. Determine the limits, or interval, that make up each category

4. Using the ordered array, count and record the number of observations

Width =

Max - min / # of categories

When creating a frequency table, the original observations are lost in the grouping process, but you gain...

the power of interpretation that you don't have with the original list of raw numbers

Histogram

a visual representation of numerical data where the horizontal axis represents the values of the variable of interest and the vertical axis (or the height of the bars) represents the frequencies or relative frequencies in each of the category.

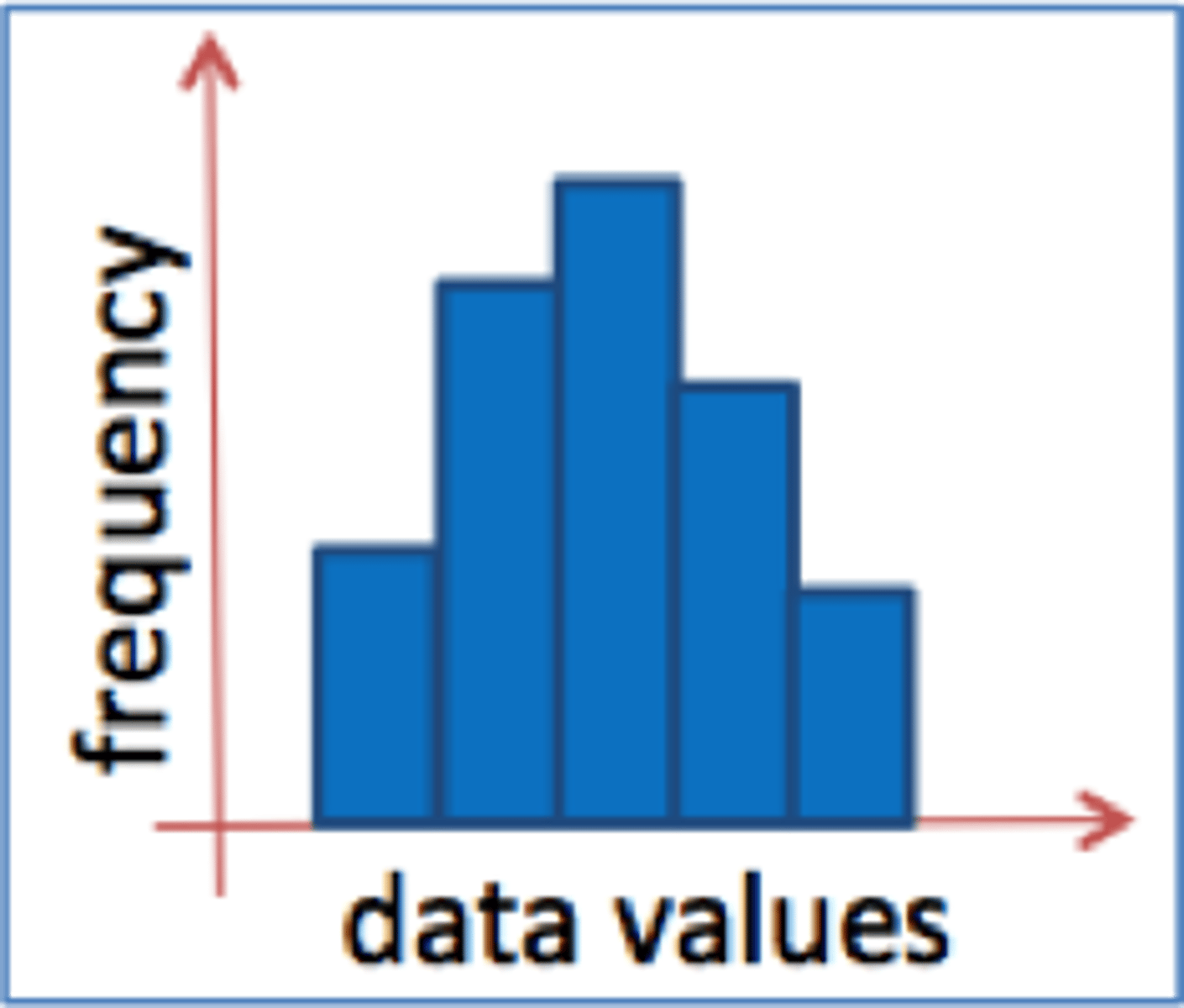
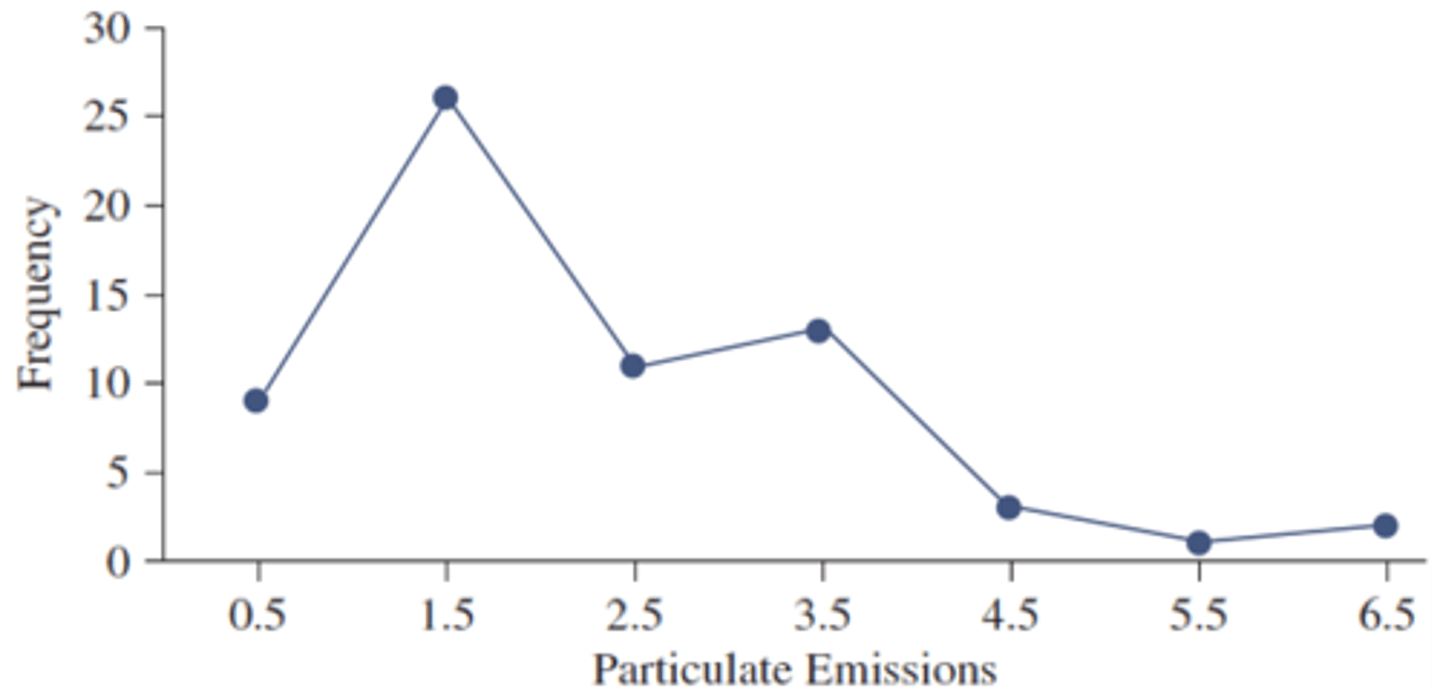
Frequency Polygon

alternative to histogram, formed by connecting the midpoints at the top bar of each category, then anchoring on the x-axis on each side, maintaining the same width

If you have too many categories, where the frequencies in each category are low, your resulting histogram may suffer from the...

pancake effect (a histogram that is too wide and flat)

If you have too few categories, the frequencies will 'pile up' in those categories, and you may see the ______________ _______________ within your histogram results

skyscraper effect (a histogram that is tall and narrow)

Ogive

a graphical representation of cumulative values (either cumulative frequencies or cumulative relative frequencies), where the X-coordinates represent the upper limit of each category, and the Y-coordinates represent the cumulative values in the corresponding category

A Stem-and-Leaf Diagram

separates data into leaves, each made up of the right most single digit of each number, and the stems, made up of the leftmost remaining digits of each number after the leaf has been lopped off

Four attributes of steam and leaf diagram

1. is most effective for relatively small data sets

2. can be used to determine minimum, maximum, range, mode, and shape

3. gives an idea of how the individual values are distributed across the range of the data

4. retains all the original data so that each observation remains distinctly identifiable

The numeric indices describe three major properties of numeric data:

1. Center

2. Variation (Dispersion or Spread)

3. Shape

Measures of Center

are used to describe a typical value, the center, and where data seem to cluster.

There are three types: (1) mean, (2) median, and (3) mode

When describing the histogram, the _______ is the balance point of histogram.

It is calculated by adding all the observations and dividing the sum by the total number of observations in the data set.

mean

Population mean, denoted by µ, is calculated using:

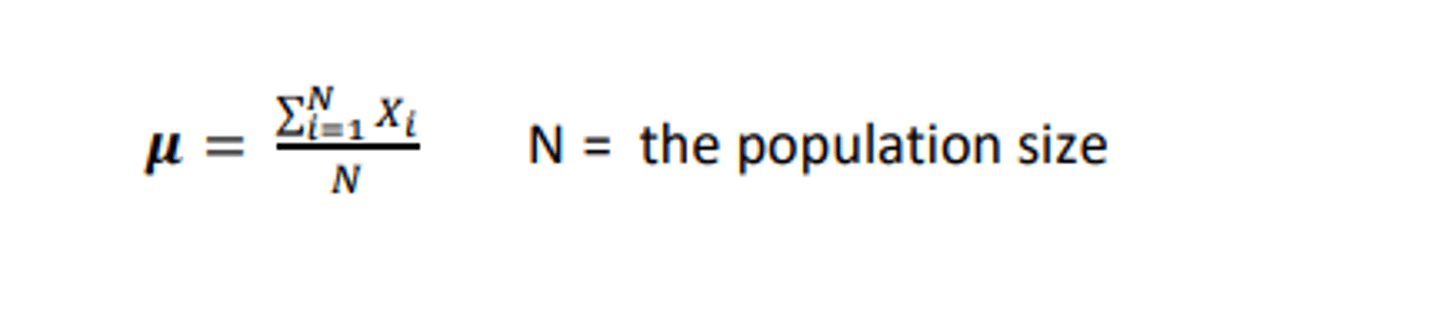
Sample mean is calculated using:

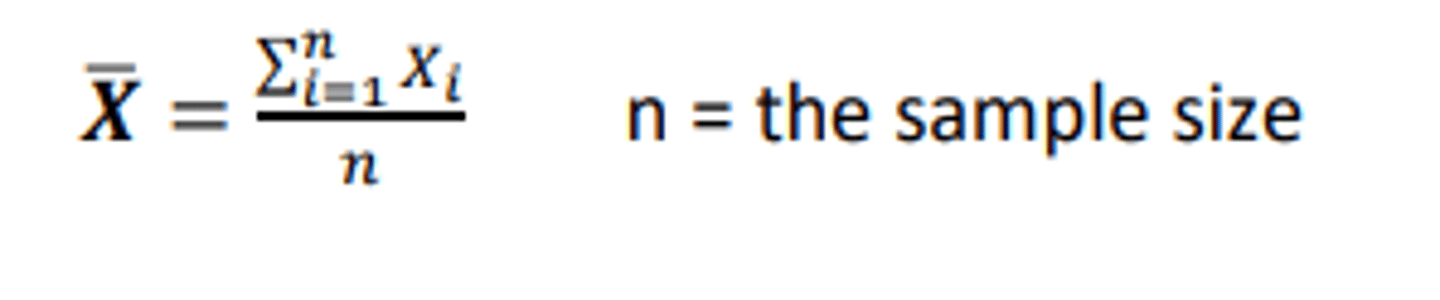
median

the point, in an ordered array, at which half the data lie above and half the lie below.

the median is calculated:

n = size of data set

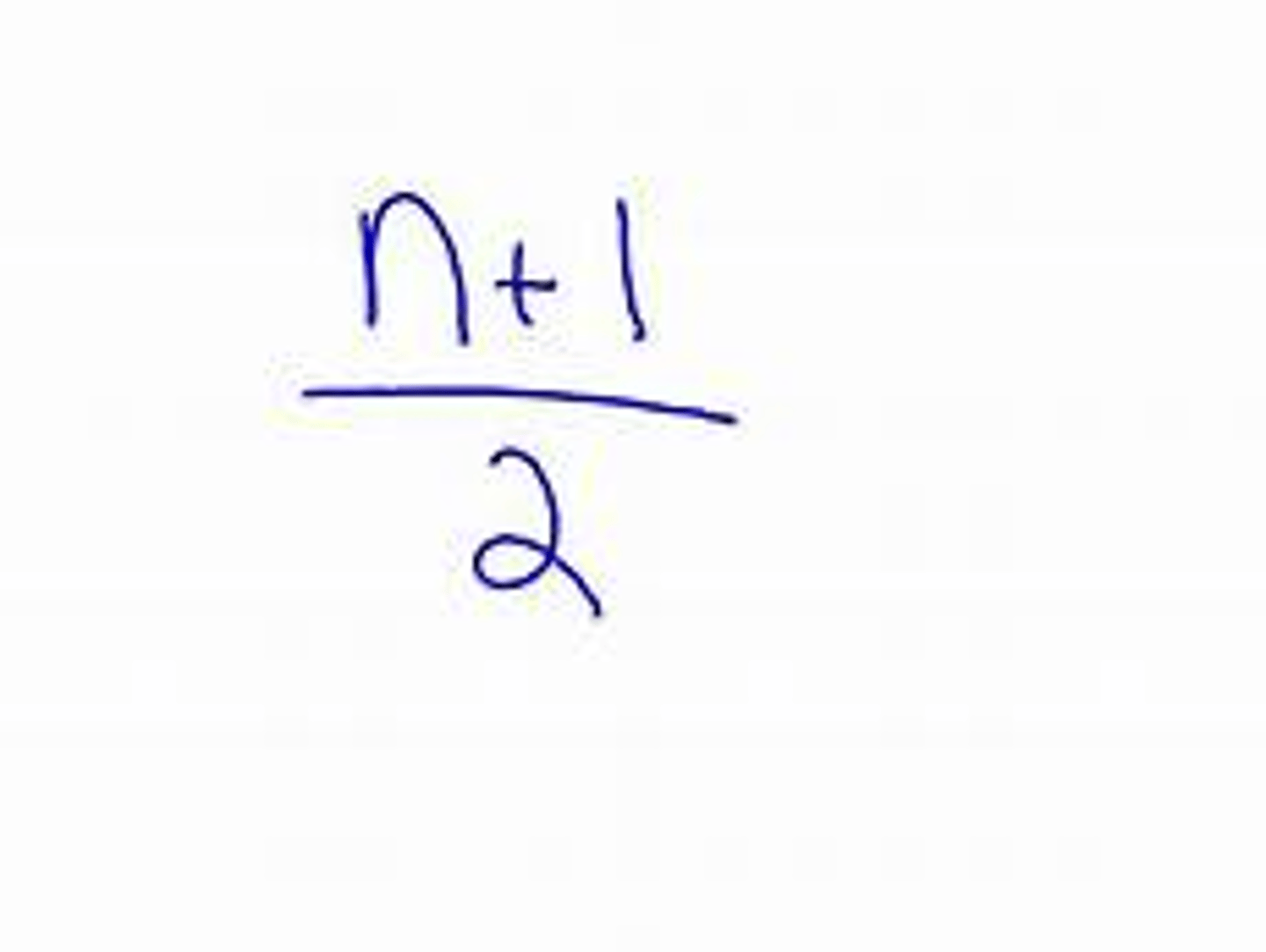
If the size of the data set is _________, the median is the average of the two middle

even

If the size of the data set is _________, the median is the middle value.

odd

the _________ is a better reflection of the center when data are skewed or have outliers.

median

Mode

the data value that occurs most often

Measures of variation are used to

describe the spread or dispersion of the data.

3 measures of variation

(1) range, (2) variance, and (3) standard deviation.

Range

the difference between the maximum value and the minimum value and is influenced by outliers

Variance

a measure of variability that utilizes all data values and reflects how the observations vary or deviate from the mean.

population variance formula

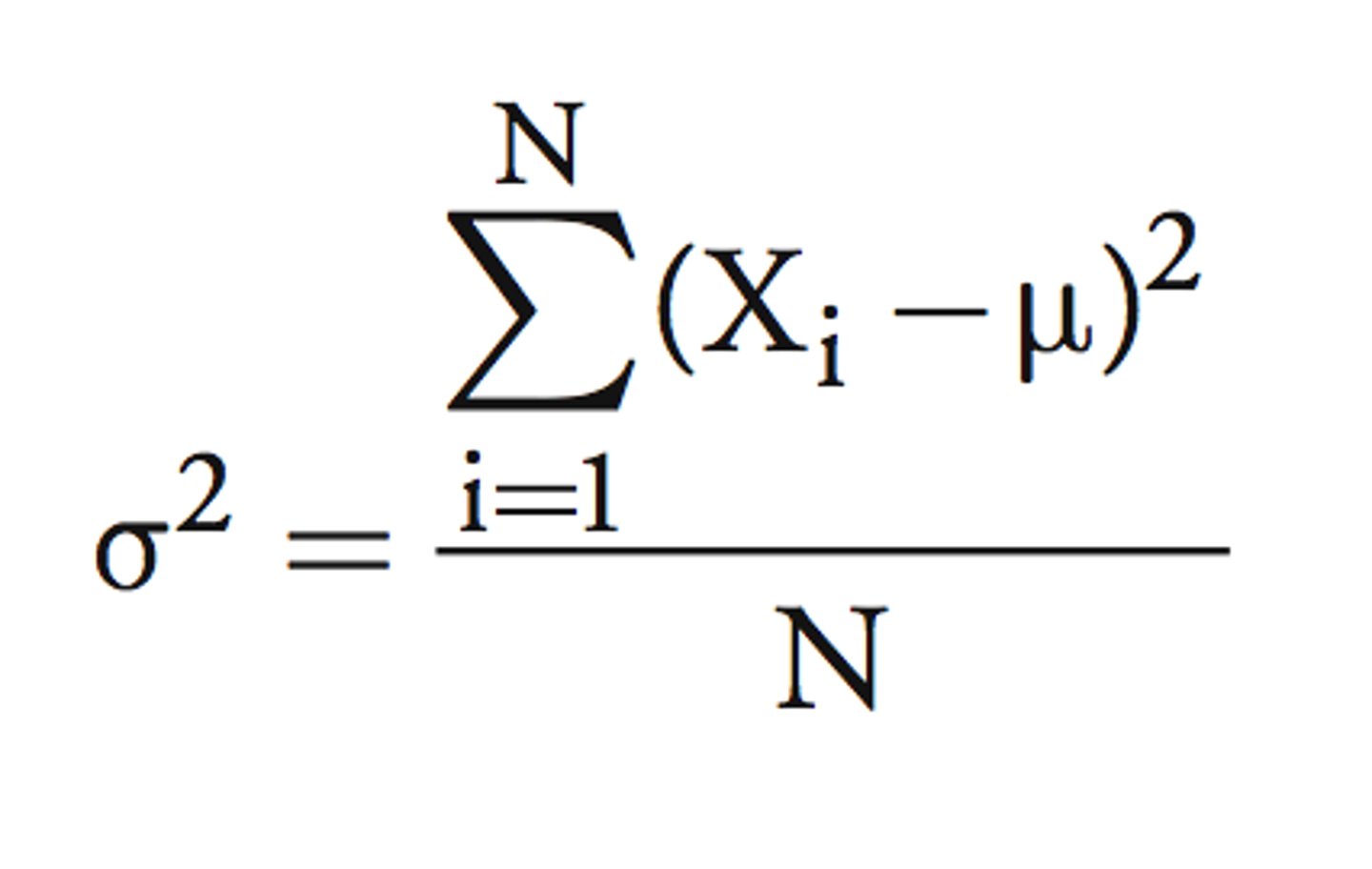
sample variance formula

Characteristics of both the population and sample variances:

(1) Both population and sample variances are influenced by outliers.

(2) Both are either zero or positive (never negative).

(3) As data spread out, variance increases.

(4) As data become more concentrated, variance decreases. (5) Data where all values are the same have no variation (variance = 0).

Standard deviation

- square root of variance

Sample standard deviation (s)

the square root of the sample variance

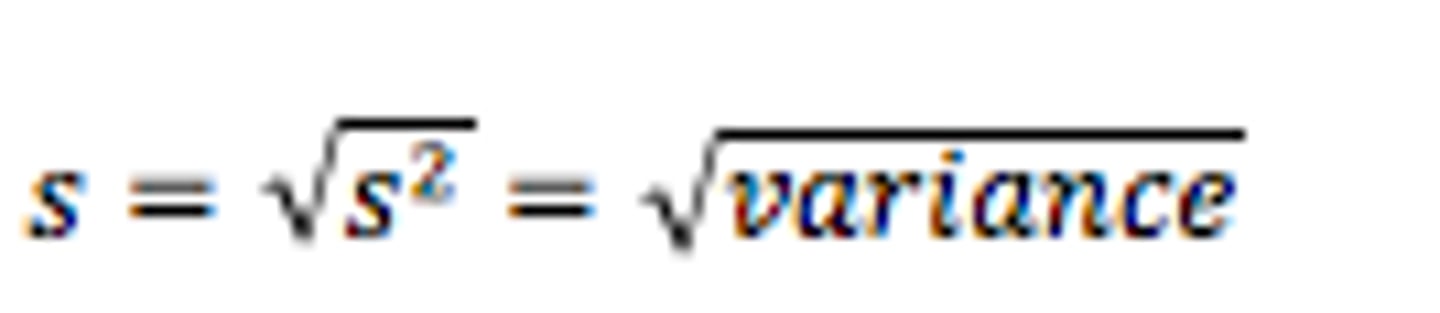
Population standard deviation

the square root of the population variance

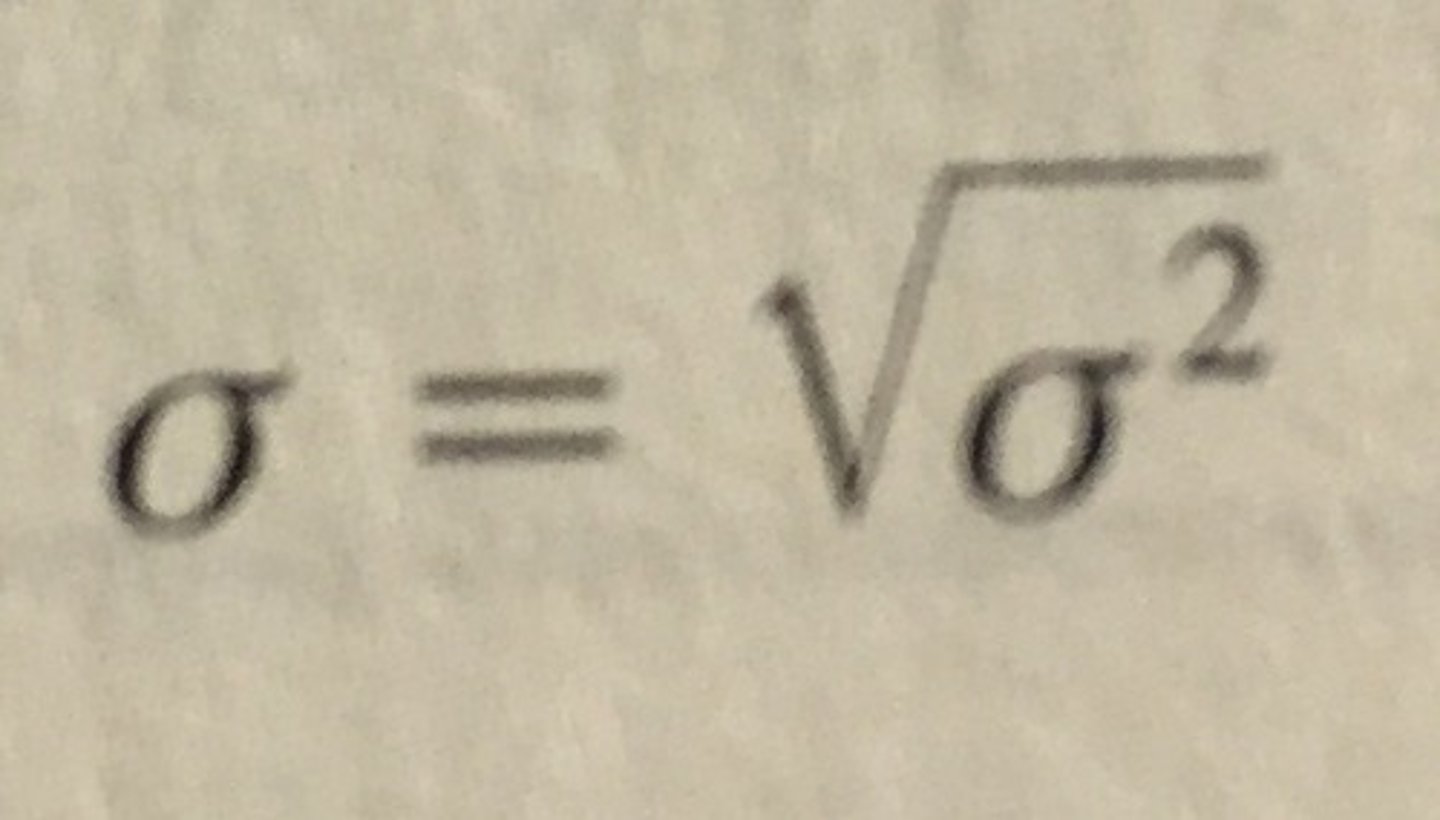
The Shape describes the .

distribution or pattern of the values within the dataset

The shape of data is either

symmetric or skewed

Data are considered __________ if one half of the data is a mirror image of the other half

symmetric

Data are considered skewed if they are

not symmetric and are considered either right-skewed or left-skewed

if mean > mode, median > mode, then the data are

right-skewed

How often does mean > median > mode and what skew

most of the time, right skewed

If mean < mode, median < mode, then the data are; and most of the time:

left skewed

How often does mean < median < mode and what skew

most of the time, left skewed

The Z-Score is a

measure of relative location that describes how far an individual observation is from the mean

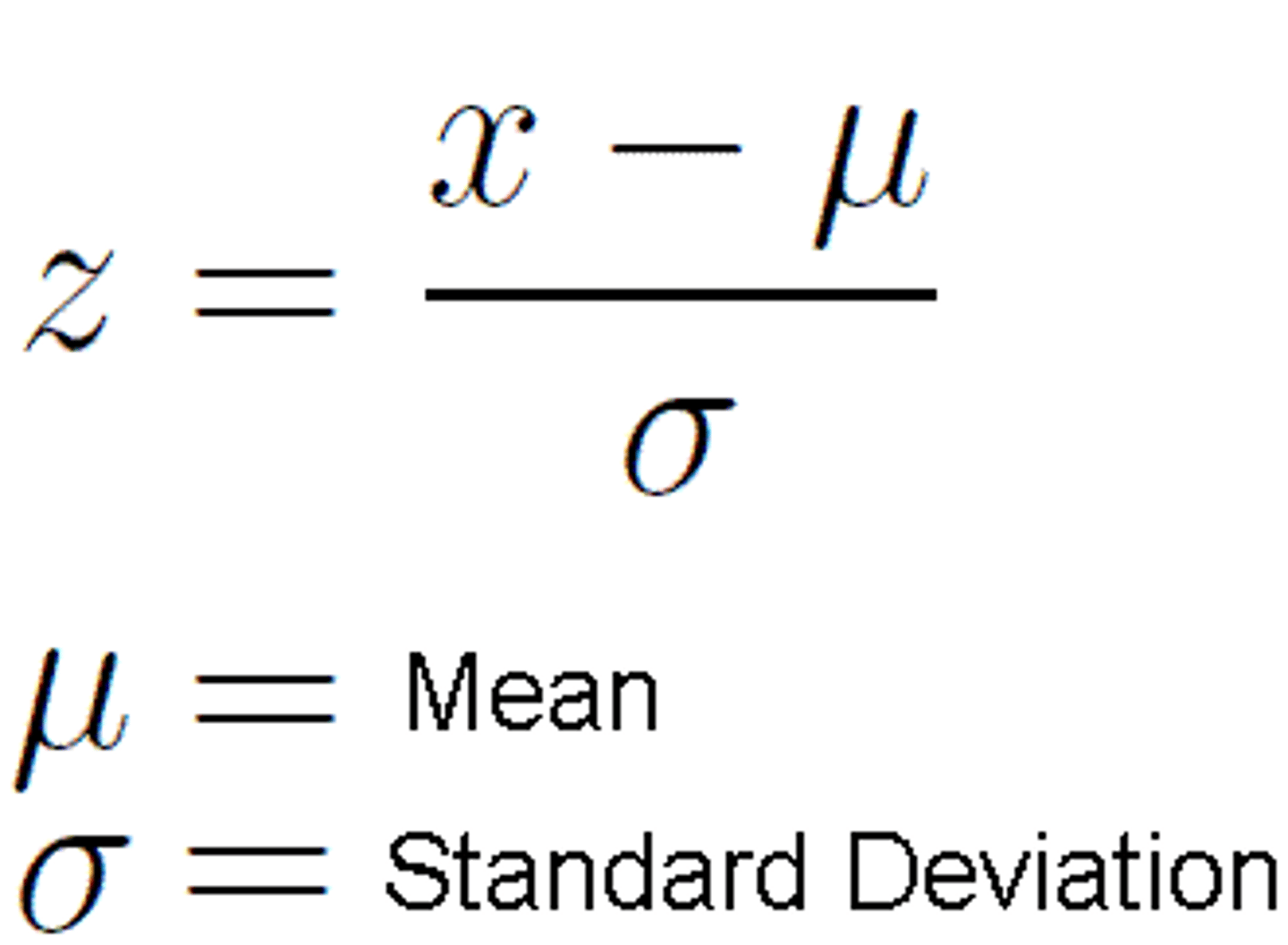
sample z-score

When data are bell-shaped, probabilities about the distance from the mean can be estimated using the

Empirical Rule

Approximately __% of the observations are within 1 standard deviation of the mean

68

Approximately ___% of the observations are within 2 standard deviations of the mean

95

Approximately ___% of the observations are within 3 standard deviations of the mean (𝑋𝑋� ± 3).

100

outlier

A value that "lies outside" (is much smaller or larger than) most of the other values in a set of data.

Outlier Rule

Upper Bound = Q3 + 1.5(IQR)

Lower Bound = Q1 - 1.5(IQR)

IQR = Q3 - Q1