Chapter 10: Sequences and Series

A. Sequences of Real Numbers

• An infinite sequence is a function whose domain is the set of positive integers, and is often denoted simply by an.
• The sequence defined, for example, by an=1/n is the set of numbers 1,1/2,1/3,…,1/n,….
  • The elements in this set are called the terms of the sequence, and the nth or general term of this sequence is 1n.
  • A sequence an converges to a finite number L if limn→∞ an=L. If an does not have a (finite) limit, we say the sequence is divergent.

Example:

Does the sequence an=1/n converge or diverge?

SOLUTION: limn→∞ 1/n=0; hence the sequence converges to 0.

B. Infinite Series

B1. Definitions

If an is a sequence of real numbers, then an infinite series is an expression of the form

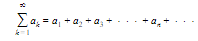
• The elements in the sum are called terms; an is the nth or general term of the series.

Example :

The p-series with p = 1 is called the harmonic series:

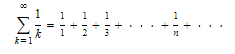
B2. Theorems about Convergence or Divergence of Infinite Series

• THEOREM 2a

  • If ∑ak converges, then limn→∞an=0.

• THEOREM 2b

  • A finite number of terms may be added to or deleted from a series without affecting its convergence or divergence; thus

  

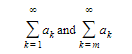
(where m is any positive integer) both converge or both diverge. (Note that the sums most likely will differ.)

• THEOREM 2c

  • The terms of a series may be multiplied by a nonzero constant without affecting the convergence or divergence; thus

  

both converge or both diverge. (Again, the sums will usually differ.)

• THEOREM 2d
  • If ∑an and ∑bn both converge, so does ∑(an + bn).
• THEOREM 2e
  • If the terms of a convergent series are regrouped, the new series converges.

B3. Tests for Convergence of Infinite Series

• THE nth TERM TEST
  • If limn→∞an≠0lim�→∞��≠0, then ∑an diverges.

Example:

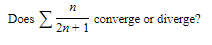
SOLUTION:

• THE GEOMETRIC SERIES TEST

  • A geometric series ∑arn converges if and only if |r| < 1.
  • If |r| < 1, the sum of the series is a1−r.
  • The series cannot converge unless it passes the nth Term Test; limn→∞arn=0 only if |r| < 1. As noted earlier, this is a necessary condition for convergence, but may not be sufficient.

  

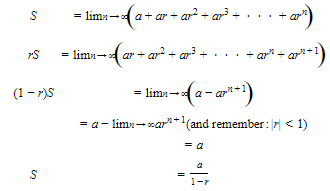
Example :

Does 0.3 + 0.03 + 0.003 + . . . converge or diverge?

SOLUTION:

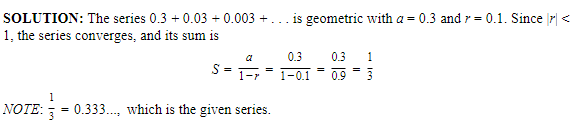
B4. Tests for Convergence of Nonnegative Series

The series ∑an is called a nonnegative series if an ≥ 0 for all n.

• THE INTEGRAL TEST
  • Let ∑an be a nonnegative series. If f(x) is a continuous, positive, decreasing function and f(n) = an, then ∑an converges if and only if the improper integral ∫∞1f(x) dx converges.

Example:

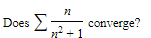
SOLUTION: The associated improper integral is

\n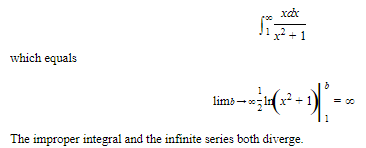

• THE COMPARISON TEST
  • We compare the general term of ∑an, the nonnegative series we are investigating, with the general term of a series, ∑un, known to converge or diverge.

(1)If ∑un converges and an ≦ un, then ∑an converges.

(2)If ∑un diverges and an ≧ un, then ∑an diverges.

Any known series can be used for comparison. Particularly useful are p-series, which converge if p > 1 but diverge if p ≦ 1, and geometric series, which converge if |r| < 1 but diverge if |r| ≧ 1.

Example :

Does ∑1/1+n4 converge or diverge?

Solution:

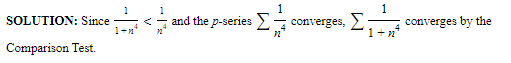
B5. Alternating Series and Absolute Convergence

Any test that can be applied to a nonnegative series can be used for a series all of whose terms are negative. We consider here only one type of series with mixed signs, the so-called alternating series. This has the form:

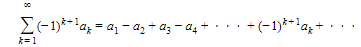
where ak > 0.

The series

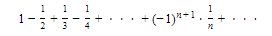
is the alternating harmonic series.

• THE ALTERNATING SERIES TEST
  • An alternating series converges if

(1)an + 1 < an for all n

(2)limn→∞an=0

Example:

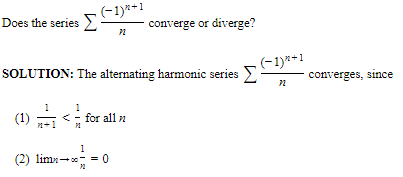
• ABSOLUTE CONVERGENCE AND CONDITIONAL CONVERGENCE
  • A series with mixed signs is said to converge absolutely (or to be absolutely convergent) if the series obtained by taking the absolute values of its terms converges; that is, ∑an converges absolutely if ∑|an| = |a1| + |a2| + . . . + |an| + . . . converges.
  • A series that converges but not absolutely is said to converge conditionally (or to be conditionally convergent). The alternating harmonic series converges conditionally since it converges, but does not converge absolutely. (The harmonic series diverges.)

Example:

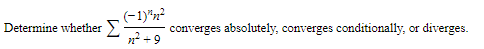
Solution:

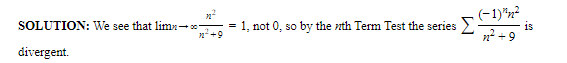
C. Power Series

C1. Definitions; Convergence

An expression of the form

where the as are constants, is called a power series in x; and

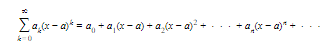
is called a power series in (x − a).

• RADIUS AND INTERVAL OF CONVERGENCE
  • If power series (1) converges when |x| < r and diverges when |x| > r, then r is called the radius of convergence. Similarly, r is the radius of convergence of power series (2) if (2) converges when |x − a| < r and diverges when |x − a| > r.
  • The set of all values of x for which a power series converges is called its interval of convergence. To find the interval of convergence, first determine the radius of convergence by applying the Ratio Test to the series of absolute values. Then check each endpoint to determine whether the series converges or diverges there.

Example :

Find all x for which the following series converges:

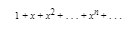
Solution:

hus, the radius of convergence is 1. The endpoints must be tested separately since the Ratio Test fails when the limit equals 1. When x = 1, (3) becomes 1 + 1 + 1 + . . . and diverges; when x = −1, (3) becomes 1 − 1 + 1 − 1 + . . . and diverges. Thus the interval of convergence is −1 < x < 1.

C2. Functions Defined by Power Series

Let the function f be defined by

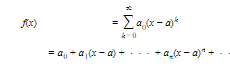
its domain is the interval of convergence of the series.

• Functions defined by power series behave very much like polynomials, as indicated by the following properties:

  • PROPERTY 2a.The function defined by (1) is continuous for each x in the interval of convergence of the series.
  • PROPERTY 2b.The series formed by differentiating the terms of series (1) converges to f ′(x) for each x within the radius of convergence of (1); that is,

  

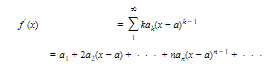
Note that power series (1) and its derived series (2) have the same radius of convergence but not necessarily the same interval of convergence.

Example:

Find the intervals of convergence of the power series for f(x) and f′(x).

SOLUTION:

• PROPERTY 2C. The series obtained by integrating the terms of the given series (1) converges to ∫xaf(t) dt for each x within the interval of convergence of (1); that is,

  

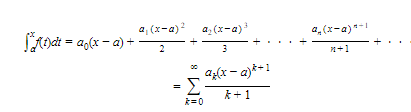
C3. Finding a Power Series for a Function: Taylor and Maclaurin Series

• If a function f(x) is representable by a power series of the form

c0 + c1 (x − a) + c2 (x − a)2 + . . . + cn(x − a)n + . . .

on an interval |x − a| < r, then the coefficients are given by

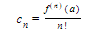
• The series

  

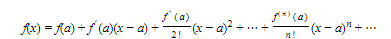
is called the Taylor series of the function f about the number a. There is never more than one power series in (x − a) for f(x). It is required that the function and all its derivatives exist at x = a if the function f(x) is to generate a Taylor series expansion.

• When a = 0 we have the special series

  

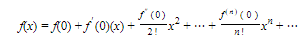
called the Maclaurin series of the function f; this is the expansion of f about x = 0.

Example:

Find the Maclaurin series for f(x) = ex.

SOLUTION:

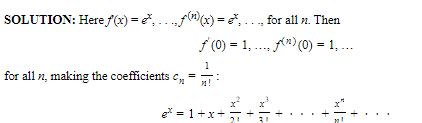
C4. Approximating Functions with Taylor and Maclaurin Polynomials

• The function f(x) at the point x = a is approximated by a Taylor polynomial Pn(x) of order n:

  

The Taylor polynomial Pn(x) and its first n derivatives all agree at a with f and its first n derivatives. The order of a Taylor polynomial is the order of the highest derivative, which is also the polynomial’s last term.

• In the special case where a = 0, the Maclaurin polynomial of order n that approximates f(x) is

  

• The Taylor polynomial P1(x) at x = 0 is the tangent-line approximation to f(x) near zero given by

  

Example :

Find the Taylor polynomial of order 4 at 0 for f(x) = e−x. Use this to approximate f(0.25).

SOLUTIONS:

C5. Taylor’s Formula with Remainder; Lagrange Error Bound

When we approximate a function using a Taylor polynomial, it is important to know how large the remainder (error) may be.

• If at the desired value of x the Taylor series is alternating, this issue is easily resolved: the first omitted term serves as an upper bound on the error. However, when the approximation involves a nonnegative Taylor series, placing an upper bound on the error is more difficult. This issue is resolved by the Lagrange remainder.

TAYLOR’S THEOREM

• If a function f and its first (n + 1) derivatives are continuous on the interval |x − a| < r, then for each x in this interval

  

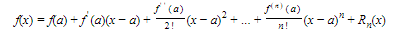
where

and c is some number between a and x. Rn(x) is called the Lagrange remainder.

Note that the equation above expresses f(x) as the sum of the Taylor polynomial Pn(x) and the error that results when that polynomial is used as an approximation for f(x).

• When we truncate a series after the (n + 1)st term, we can compute the error bound Rn, according to Lagrange, if we know what to substitute for c. In practice we find, not Rn exactly, but only an upper bound for it by assigning to c the value between a and x that determines the largest possible value of Rn. Hence:

  

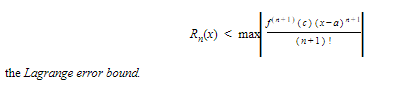
Example :

Estimate the error in using the Maclaurin series generated by e x to approximate the value of e.

SOLUTION:

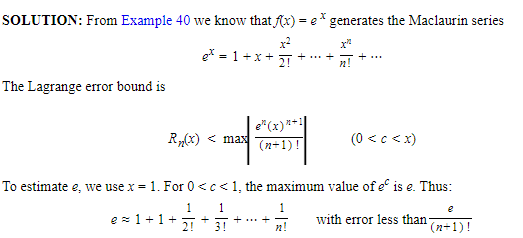
C6. Computations with Power Series

• The power series expansions of functions may be treated as any other functions for values of x that lie within their intervals of convergence.
• They may be added, subtracted, multiplied, divided (with division by zero to be avoided), differentiated, or integrated.
• These properties provide a valuable approach for many otherwise difficult computations. Indeed, power series are often very useful for approximating values of functions, evaluating indeterminate forms of limits, and estimating definite integrals.

Example:

Compute 1/√e to four decimal places.

SOLUTION:

We can use the Maclaurin series,

C7. Power Series over Complex Numbers

A complex number is one of the form a + bi, where a and b are real and i 2 = −1. If we allow complex numbers as replacements for x in power series, we obtain some interesting results.

Consider, for instance, the series

\n