Unit 9: Parametric Equations, Polar Coordinates, and Vector-Valued Functions

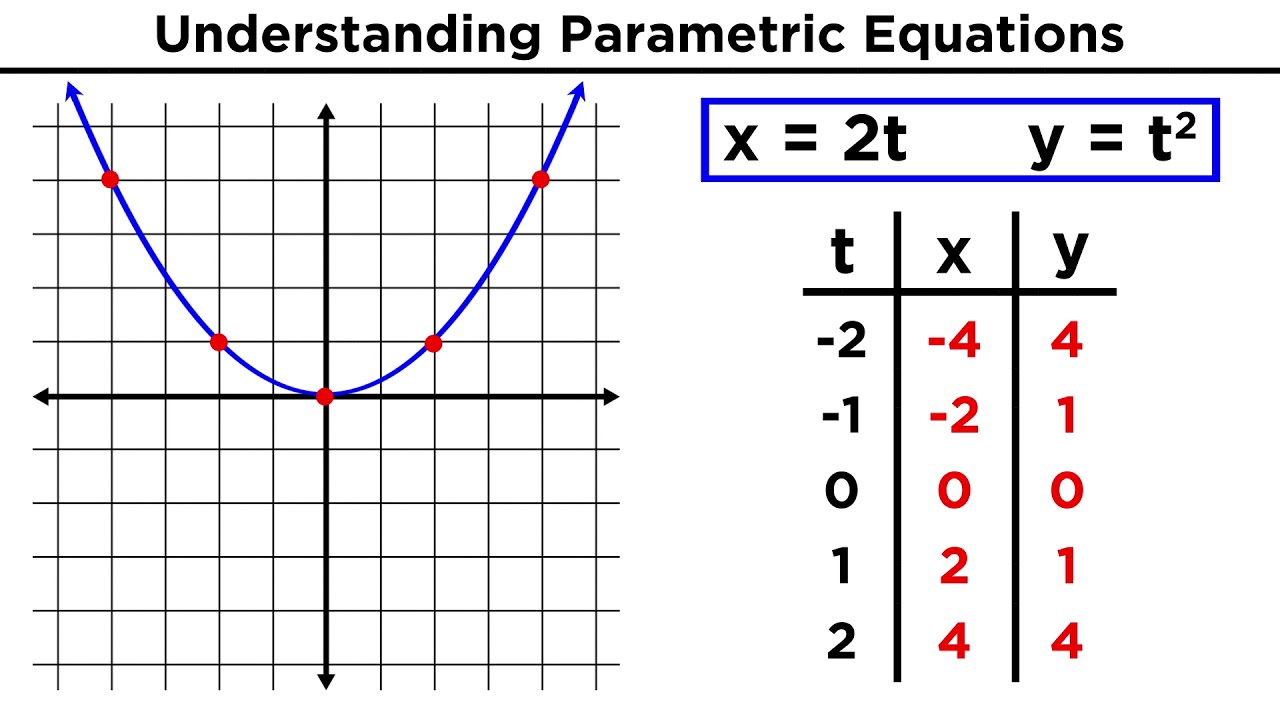
Parametric Equations

• Parametric functions show a relationship between a variable and time

  • Often it’s used to show the position of an object or shape of a curve

• The formula for a parametric equation is given by:

  • x = f(t)
  • y = g(t)

• X & Y are dependent and time is independent

  

Arc Length of Curves

• Arc length is the distance along a curve

• We have to square the derivative, but because both X & Y are dependent, we square both derivatives

• We then take the square root and the integral

  • This time it’s the integral from t=a to t=b

  

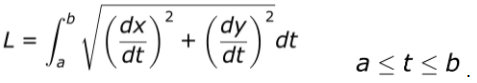
Vector-Valued Functions

• These functions map numbers to vectors!

• For parametric equations, they represent position, velocity, and acceleration!

• To derive these functions we have to take the derivative of each component individually

  

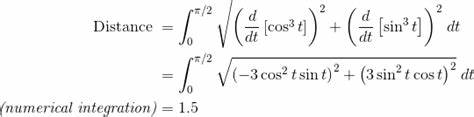
• The same applies to integration- integrate each component individually

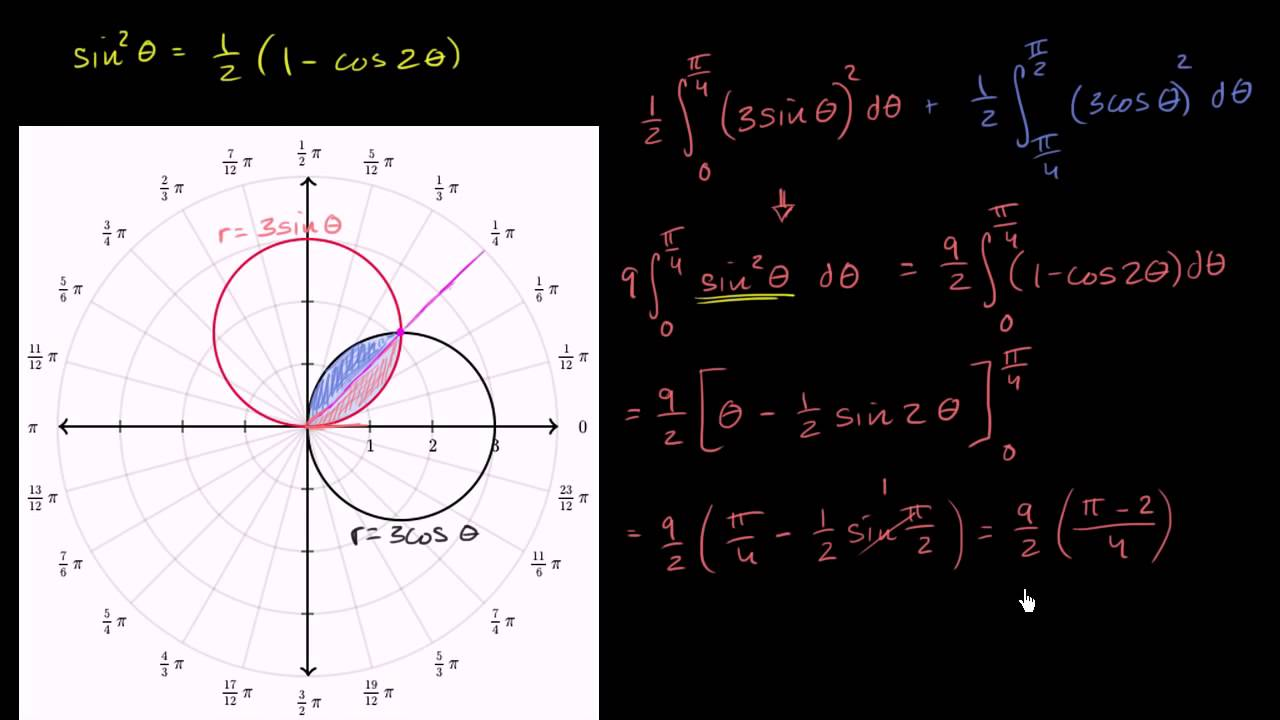
Polar Coordinates

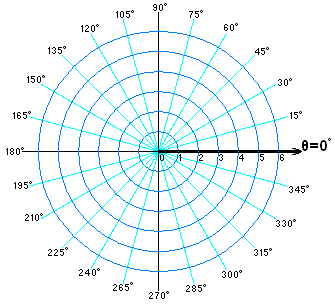
• This is a coordinate system where x,y pairs are replaced with r (the distance from the orgin) and θ (angle from x-axis)

  

• To go from a set of polar coordinates to regular (cartesian) there is a conversion:

  

• Remember that when we differentiate with polar coordinates we differentiate with respect to theta → dθ

• Area between two curves in polar coordinates is given by A = (1/2) ∫(a,b) (R^2 - r^2) dθ

  • Instead of top - bottom we have inner - outer

    \n