Unit 3: Differentiation: Composite, Implicit, and Inverse Functions
Chain Rule
When finding the derivative of a composite function, take the derivative of the outside function with the inside function g considered as the variable, leaving the “inside” function alone. Then we multiply this by the derivative of the inside function, with respect to the variable x.
- The Chain Rule: If y = f(g(x)), then y’ = f’(g(x)) * g’(x) OR
- If y = y(v) and v = v(x), then dy/dx = (dy/dv)*(dv/dx)
My personal memory trick for this is “douter, inner, dinner) → drop the power down to outside the parathesis, leave the inner, multiply by the derivative of the inner

Implicit Differentiation
When you can’t isolate y in terms of x, you take the derivative implicitly. Essentially, you solve for the derivative of x with respect to y, in order to get a derivative in terms of both variables.
- (dx/dy) = (1/(dy/dx))
Solving with the reciprocal allows to split up the variable and pair it to both sides, so that they can be factored.
- You can also apply other, previous rules like the product rule in order to solve it. The AP exam loves to do this.
An easier way of describing implicit differentiation is that if your variable doesn’t match dx, then you need to follow it up with d(variable)/dx
For example, if we’re given x^2 + y^2 = 25 at the point (3, 4), we need to implicitly differentiate → doing this with respect to x we get:
- 2x + 2y(dy/dx) = 0
Then you have to solve for dy/dx
- dy/dx = -x/y
At the point (3, 4), we have x = 3 and y = 4. Substituting these values, we get:
dy/dx = -3/4
- So the slope of the tangent line is -3/4.
- We also know that the point (3, 4) lies on the tangent line. Using the point-slope form of the equation of a line, we get:
y - 4 = -3/4(x - 3)
- This is the equation of our tangent line
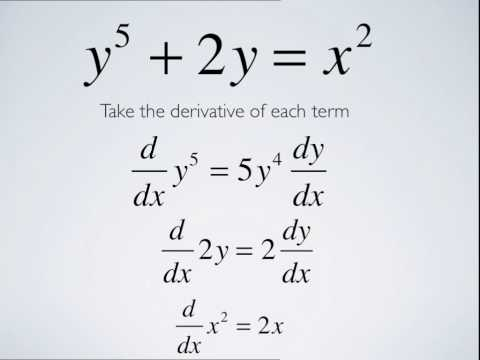
Inverse Function Differentiation
There is a simple formula in order to find the derivative of an inverse function.
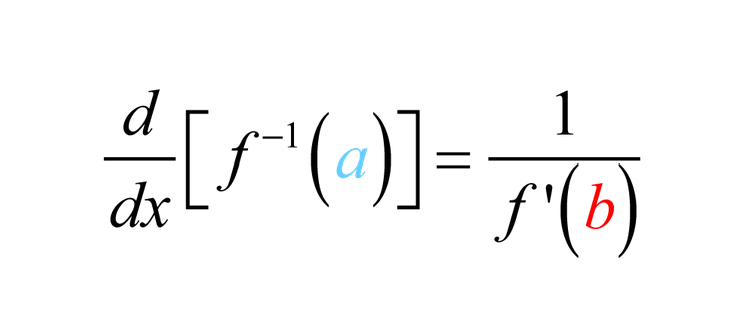
In short, we can find the derivative at a particular point by taking the reciprocal of the derivative at that point’s corresponding y value.
- Say you want the derivative at the point (1,2) - you want g’(1). So find f’(2), then take the reciprocal - this is the value of g’(1).
- Our original point is (1,2) so our reciprocal will be (2,1)
- The same goes for our slope, find the slope at f’(2) and then take the reciprocal
- Remember, f’(x) is the same as the slope!
The AP test usually only has 1-2 of these questions so don’t stress too much! 👍
Inverse Trigonometry
This is going to be one that is easier to just memorize, but you can also find them by following the formulas explained in implicit differentiation and using trigonometry rules.

HINTS
- When two terms are multiplied together, use product rule unless it’s easier to multiply it out
- If you see a function within another function, you will almost certainly have to use chain rule
- If there are x and y terms mixed together, we will need to use implicit differentiation
- If you’re finding the derivative at a point, just plug it in and avoid the solving out
- When evaluating derivatives at a point, look to see if the terms become one or zero
- You can mentally take certain derivatives
- If it is required to take a second derivative, simplify the first derivative before you start