Unit 7: Differential Equations

Introduction & Slope Fields

• In related rates we saw how we can model the change in one thing related to another with derivatives, and differential equations are similar!
  • Oftentimes, variables are not constant, so we have to represent their change using a derivative (Ex. the change in y is dy/dx)
  • A differential equation models the change in one variable with respect to another

\

• Slope fields show us what the slopes look like at points on a graph

  \

  

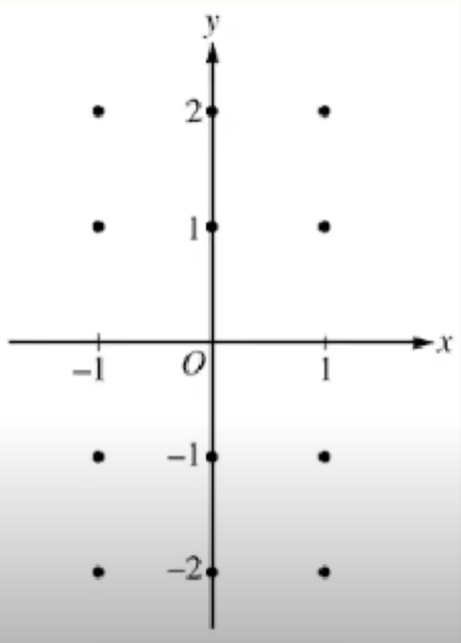
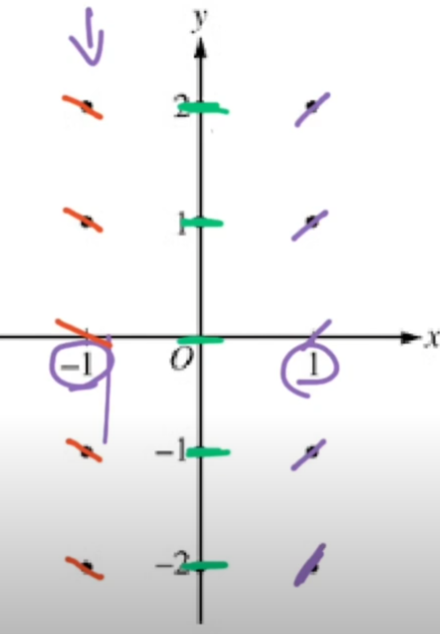
• This is for the equation dy/dx = x

  • Remember that this is a derivative so it will show us the slope at these points!

  • All you have to do to construct a slope field is plug in your x/y (or both) values into your differential equation and draw that as your slope

  • Ex. The slope at x = -1 would be -1 (because dy/dx = x)

    \

  

• The AP exam might also require you to sketch a solution curve given a slope field!

  \

  

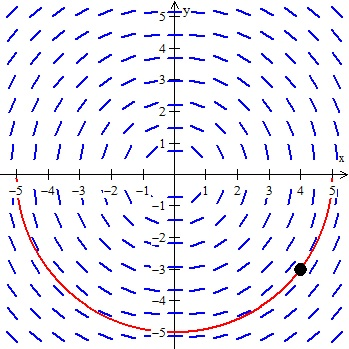
• All you have to do is “flow” with the slopes

  • Make sure you don’t cross abruptly or draw a line that doesn’t follow the slope
  • Because this is by hand, it doesn’t have to be exact, just try and go with the tangent lines!

\

Differential Equations

• If you’re given a differential equation where the derivative of a function is equal to some other function, you have to solve for the original! You can do this by taking the integral (antiderivative) of both sides!
• A good memory trick is that differential equation problems will be SIPPY problems
  • S: separate (dy and dx on separate sides)
  • I: integrate (remove the derivative)
  • P: Plus C (add your c value to your integral)
  • P: Plug in your initial condition
  • Y: Y equals (solve to find what y is)
• Example: If dy/dx = 4x/y and y(0) = 5 we need to solve for y
  • Start by separating → ydy = 4xdx
  • Then integrate → ∫ydy = ∫4xdx → y^2/2 = 2x^2 + C
  • (Make sure you add C!)
  • Plug in → (5)^2/2 = 2(0)^2 + C
  • C = 25/2
  • Now set y equals → y = 2x^2 + 25/2

\