Synoptic Exam 2 Study Guide (Concepts, Equations, etc.)

Week 6: Isentropic Analysis + Drylines

What is a dryline, and what is the typical spatial scale both in width and length?

A dryline is a boundary between dry and moist air masses.

Width: ~10 km

Length: ~100 - 1000 km

Drylines are not formally considered as fronts; however, they have some similarities and differences to them. What are they?

Similarities: Like fronts, they are boundaries between air masses of different densities.

They also exhibit cyclonic convergence along the boundary.

Differences: Unlike fronts, they have inconsistent temperature gradients that change daily.

Also, unlike fronts, they require terrain and have variable motion as they are not associated with mid-latitude cyclones.

As mentioned previously, drylines have inconsistent temperature gradients that change with the diurnal cycle. Why is that?

The specific heat of water is 5x higher than dry land. This causes changes in sensible and latent heating, which results in the diurnal change of the temperature gradient.

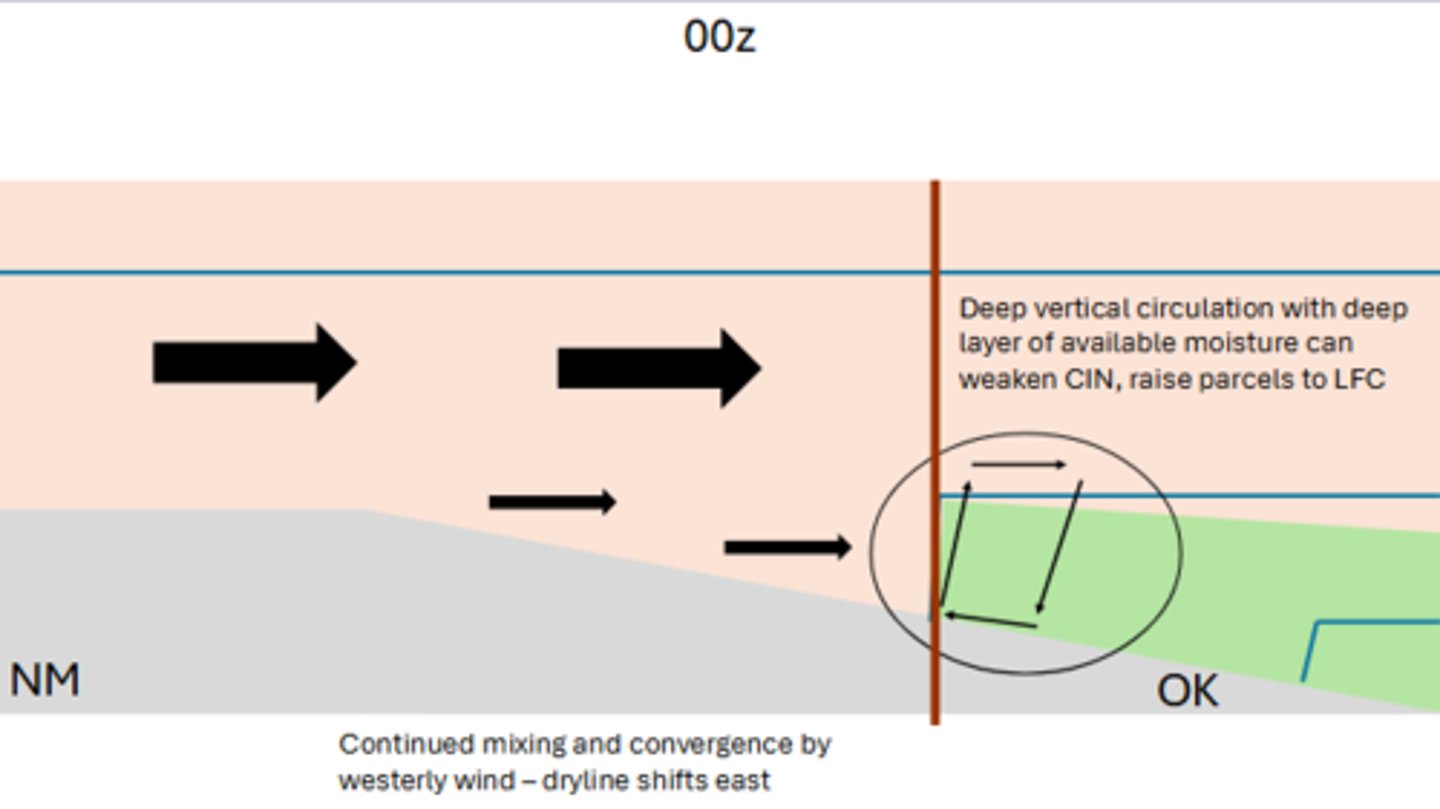
Typically, along the dryline, we see convergence at the interface between our fully mixed boundary layer (BL) and our shallower BL, which drives vertical circulation. If we have a continuation of this mixing and the convergence of our 850 mb westerlies, which cardinal direction would the dryline shift?

It would continue to shift to the EAST.

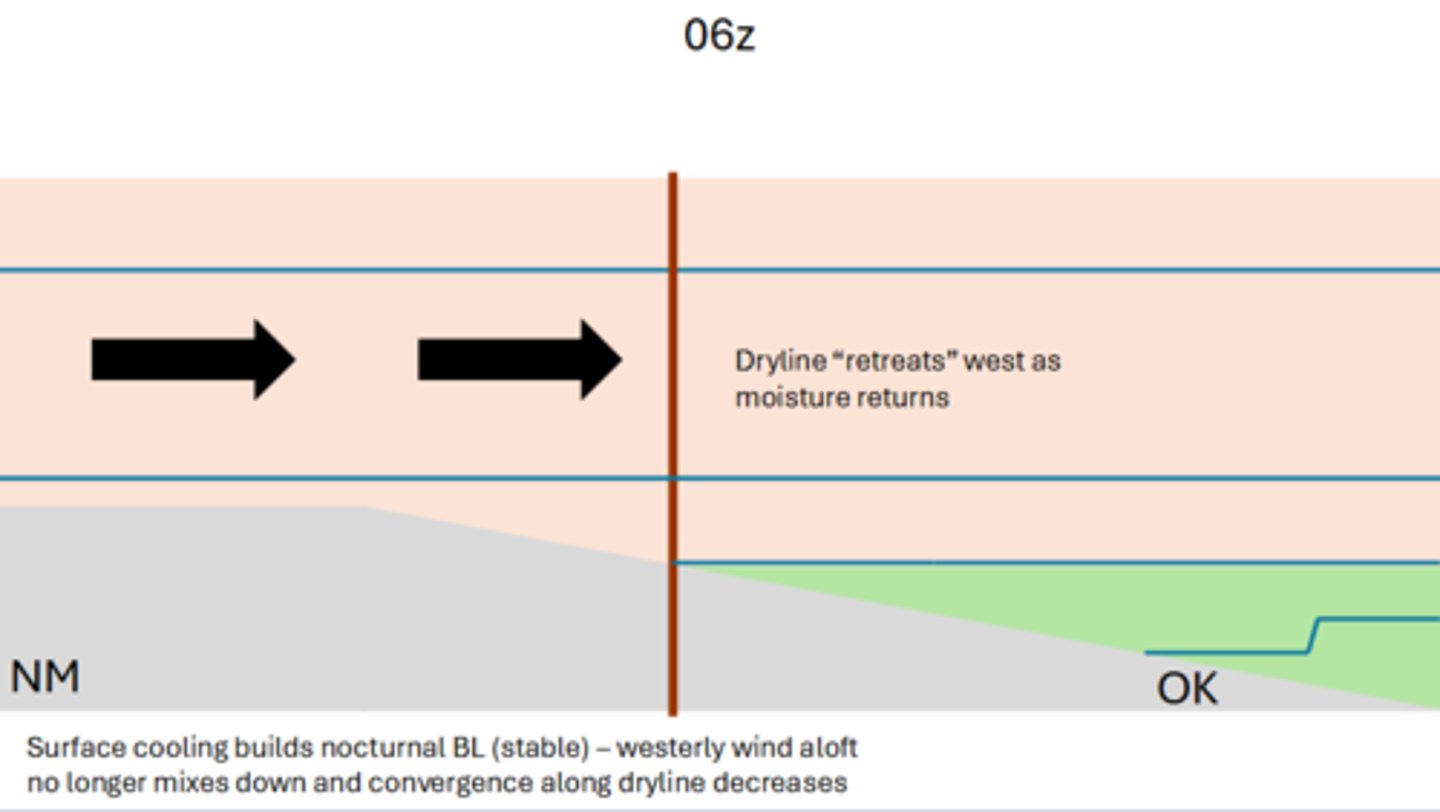
As surface cooling begins to build our nocturnal boundary layer (BL), our 850 mb westerlies no longer mix down, and convergence along the dryline decreases. Which cardinal direction does the dryline begin to retreat as moisture begins to return?

It would begin to retreat toward the WEST.

T or F: The vorticity of an isentropic surface also has a special significance, and the PV is not conserved for flow moving along isentropic surfaces.

False; The vorticity of an isentropic surface also has a special significance, and the PV IS conserved for flow moving along isentropic surfaces.

When looking at the vertical structure of potential temperature, does potential temperature increase of decrease with height?

Potential temperature INCREASES with height.

Note: This is true except in cases of adiabatic/superadiabatic near-surface layers.

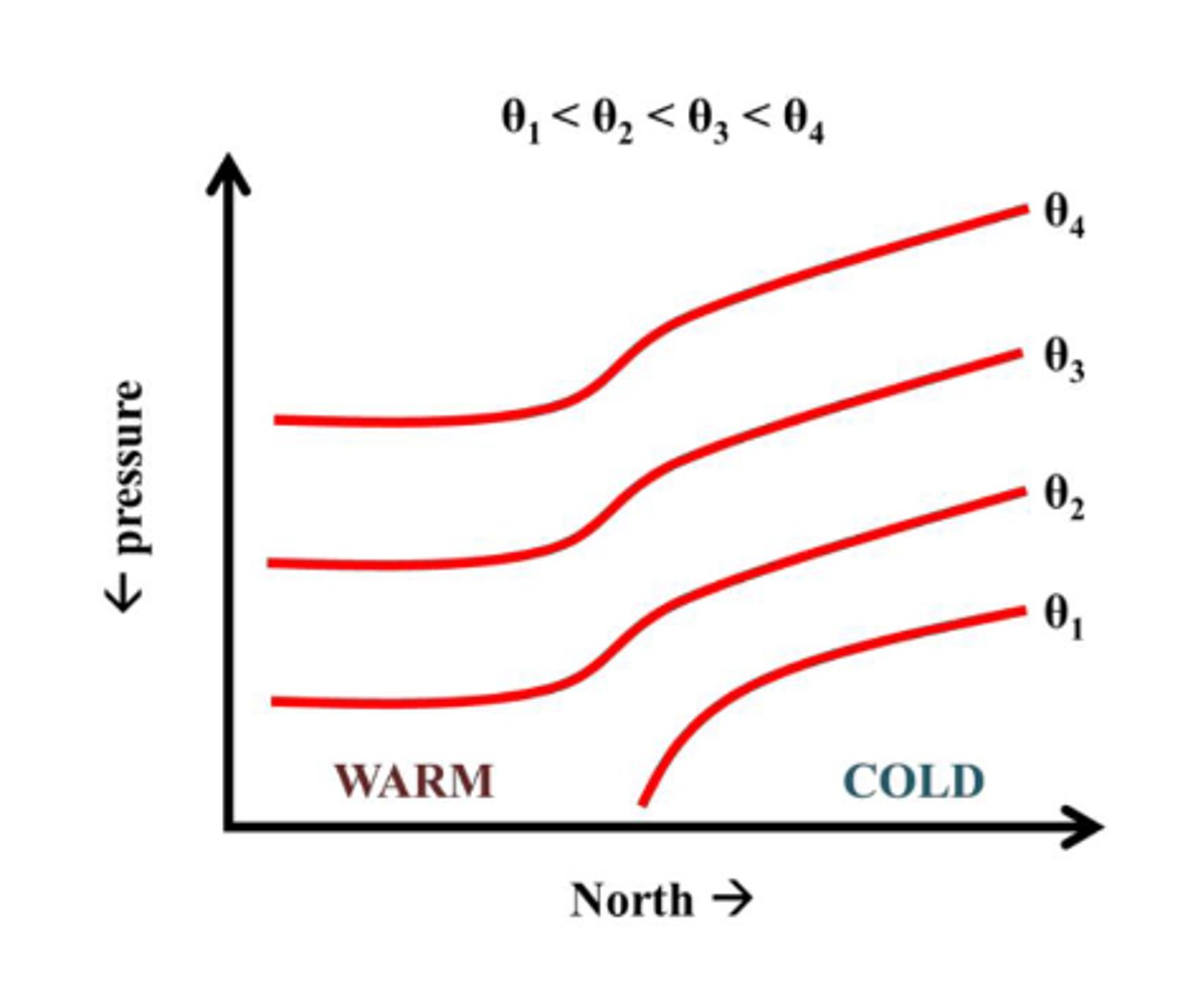
If we have colder temperatures on an isobaric surface, what kind of potential temperature does this correspond to?

Lower or colder potential temperature

Which direction do isentropic surfaces slope over colder air?

They slope UPWARD over colder air.

Looking at the expression for isentropic vertical motion, what does each term represent?

ω = (∂p/∂t)θ + V ⋅ ∇(θ)p + ∂p/∂θ (∂θ/∂t)

1st term: Local pressure tendency (on an isentropic surface)

2nd term: Pressure advection (on an isentropic surface)

3rd term: Diabatic heating/cooling

Looking at the first term in our expression for isentropic vertical motion, what are the assumptions for the "frozen wave" approximation?

(∂p/∂t)θ

The assumptions for this approximation are the following:

1.) The local rate of change of pressure is due entirely to the synoptic system's motion (e.g., neglect changes to intensity, neglect the diurnal cycle impact on pressure)

2.) System not changing speed of movement or shape in time

T or F: If we are in a reference frame moving with a synoptic-scale weather system (not flow), our first term of the isentropic vertical motion equation would be zero.

True

Typically the second term or the pressure advection term dominates, making our full equation the following

ω = V ⋅ ∇(θ)p

Looking at this equation, what sort of pressure advection leads to rising motion? Sinking motion?

Hint: What sign is advection?

Positive pressure advection (high to low pressure) leads to ASCENT.

-V ⋅ ∇(θ)p > 0 => ω < 0

Negative pressure advection (low to high pressure) leads to DESCENT

-V ⋅ ∇(θ)p < 0 => ω > 0

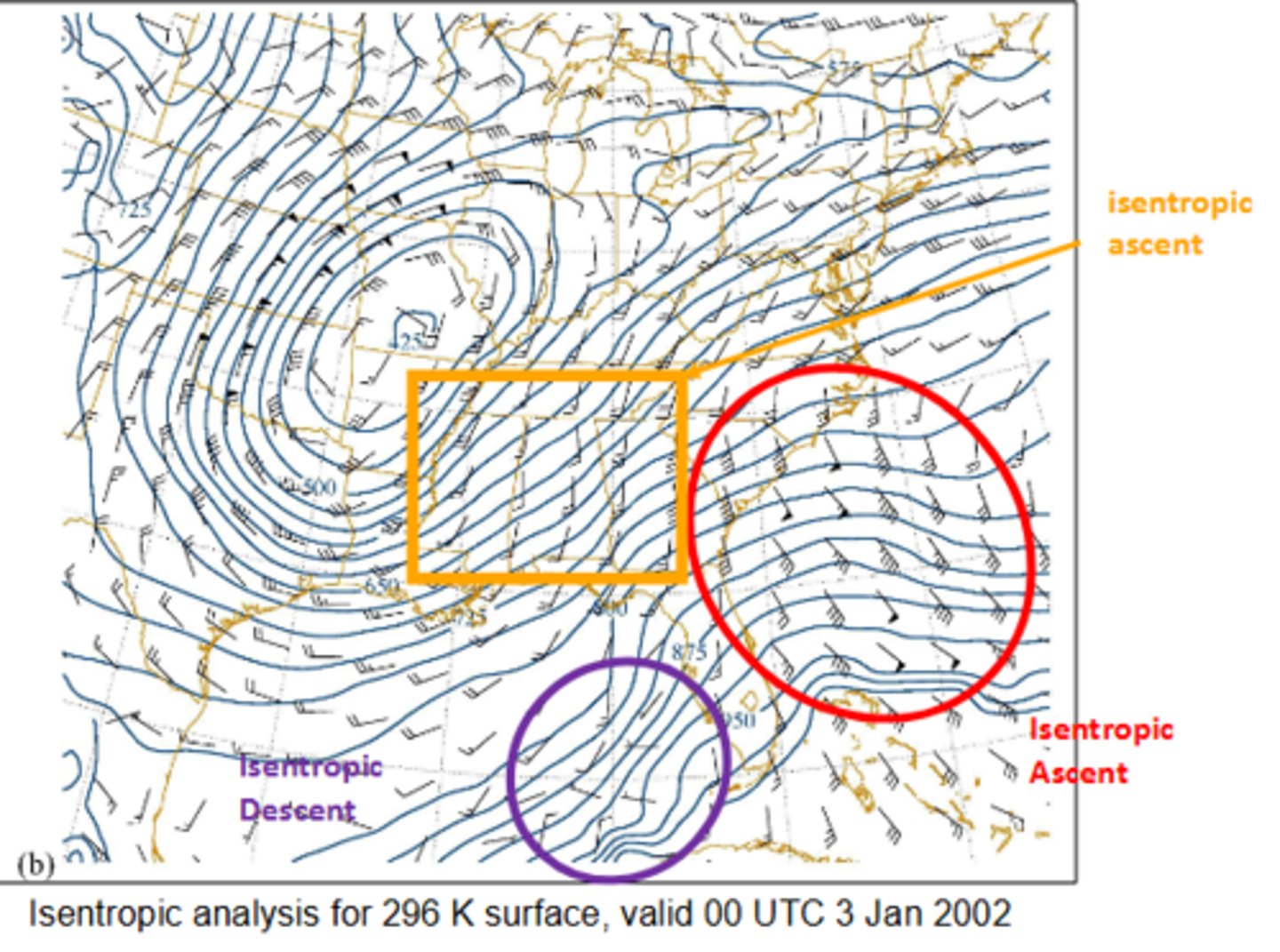
When evaluating isentropic ascent and descent on an isentropic map, where we see wind barbs going across higher isobars to lower isobars, we would expect what isentropic ascent or descent?

Where we see wind barbs going across lower isobars to higher isobars, we would expect isentropic ascent or descent?

Isentropic ascent (rising motion)

Isentropic descent (sinking motion)

Looking at the third term from our isentropic vertical motion equation, we can shift our perspective to a parcel.

∂p/∂θ (∂θ/∂t)

Following our parcel, it is constrained to move on an isentropic surface only until it reaches what? After that, on what surface does our parcel move on?

Until it reaches the LCL, after it reaches the LCL, it moves on a θe surface. (equivalent potential temperature)

Moisture is transported in which direction along the isentropic surface?

It is transported upward along the isentropic surface

What are some advantages of the isentropic approach?

Synoptic-scale flow is approximately isentropic

Conceptually straightforward, explicit representation of vertical motion on horizontal maps

Adiabatic assumption is quite good much of the time, and even when it is notvalid the qualitative answer remains unchanged.

Can simplify the vorticity equation

What are some disadvantages of the isentropic approach?

Doesn't work well in places where Θ is constant (or decreasing) with height. (e.g., near the surface, where vertical mixing, sensible heat, and radiation play important roles.)

Isentropic surfaces can intersect the ground (and because they have a greater tilt, they do so more frequently than isobaric surfaces!)

Require a coordinate transformation from constant height or isobaric coordinates

The range of isentropic surfaces to look at varies by season (and event). Generally, warmer (300+ K) during warm season, cooler (290-295 K) in cool seasons.

Week 7: Vorticity and Rossby Waves

Label the following equations:

1.) ζ = k ⋅ ∇ x u = ∂v/∂x - ∂u/∂y

2.) η = ζ + f

1.) Vertical Relative Vorticity

2.) Vertical Absolute Vorticity

Note: We mainly focus on the vertical, but there are 3D versions of the above equations

What is the Rossby Number, and what does it measure? What is the equation?

Non-dimensional number that provides a measure of the magnitude of the acceleration due to the Coriolis force.

It measures the degree of geostrophy, specifically, smaller the number, the more valid the approximation.

R0 = U/f0L

Looking at the barotropic vorticity equation for a frictionless, barotropic atmosphere, all terms with vertical motion and friction are neglected. This leaves us with the following equation:

Dh(ζ + f)/Dt = 0

If we are then following the flow, what happens to our absolute vorticity?

Our absolute vorticity remains constant

What is the restoring force for a wave?

It is simply the fact that f increases from the equator to the poles.

Note: This is also called the beta effect, where β = f/y

Long waves move fast or slowly around the globe? Short waves?

Long waves move SLOWLY, while short waves move FASTER and progress through the longwave.

T or F: For wavelengths with mid-latitude cyclones:

U > βL^2 > 4π^2

waves propagate westward relative to the Earth, but eastward relative to the mean zonal flow.

False; For wavelengths with mid-latitude cyclones:

U > βL^2 > 4π^2

waves propagate EASTWARD relative to the Earth, but WESTWARD relative to the mean zonal flow.

What is the typical synoptic-scale disturbance of the zonal wavelength? Rossby wave speed? Mean zonal wind?

Zonal wavelength: of order 6000 km

Rossby wave speed: ~ 9 m/s

Mean zonal wind: generally westerly and >9 m/s

Systems that move in the same direction as the basic current progress or regress? Systems that move in the opposite direction?

Progress; Regress (Retrograde)

What 4 things can cause Rossby waves?

1.) Flow over topography

2.) Latent heating with recurving tropical cyclones

3.) Baroclinic instability of zonal current

4.) Downstream development

What are some characteristics of long waves?

Typically 4-6 around the globe at any given time

Wavelength varies from 4000 - 8000 km

Stationary or moves very slowly

The geostrophic advection of planetary vorticity is much greater than the geostrophic advection of relative vorticity in long waves (small R0)

What are some characteristics of short waves?

Short waves are embedded in the long waves

They move quickly to the east

Weaken when they move through a long-wave ridge; strengthen when they move through a long-wave trough

Short waves are identified in the upper-level flow as (local) maxima of absolute vertical vorticity

The advection of relative vorticity is comparable to, or sometimes even much larger than, the advection of planetary vorticity for shortwaves

Since cold air is denser, the depth of a column of air is less or more than that of warm air at the same pressure? What equation is defined by the relationship between thickness and temperature?

It is LESS than that of warm air

The Hypsometric Equation

Z2 - Z1 = RdTv/g0 ln(p1/p2)

What is the link between fronts and jet streams?

Jet stream aloft is due to thermal contrasts below, while fronts are zone of thermal constrast.

What is the expression for thermal wind and what does it reveal about vertical shear of the geostrophic wind?

∂Vg/∂p = -R/pk x ∇pT

It reveals that for the vertical shear of the geostrophic wind is directly proportional to the horizontal temperature gradient.

Week 8: Jets

What is the AMS glossary definition of a jet stream?

A jet stream is defined to be relatively strong winds concentrated within a narrow stream in the atmosphere.

What is the polar jet? Where does the polar jet move meridionally and vertically with the seasons?

It is the band of meandering strong winds (~100 knots) found at the tropopause

It moves meridionally (30-60 latitude) and vertically (10-15 km)

What is the subtropical jet? Where is it typically found, and where does it move to?

It is associated with the subtropical front between the tropical and mid-latitude air masses and the Hadley Cell circulation.

It is usually found between 25 and 30 N. It does not meander as much as the polar jet does, but it has been observed as far north as 60 N.

What are jet streaks?

Jet streaks are local maxima of wind speed (isotach maximum) in the jet stream.

T or F: Jet streaks influence upper-level divergence/convergence and resultant vertical motion.

True

Jet streaks propagate at a speed that is slower than the speed of the wind itself. What does this do to the air parcels upstream of the jet streak and downstream of the jet streak?

Air parcels tend to ACCELERATE just upstream from the jet streak in the ENTRANCE region

Air parcels tend to DECELERATE just downstream of the jet streak in the EXIT region

What two methods can be used to diagnose vertical motion with jet streaks?

1.) Parcel method

2.) Omega equation

As air parcels enter the stronger pressure gradient, they ___. However, they ___ as they leave the jet maxima.

accelerate, decelerate

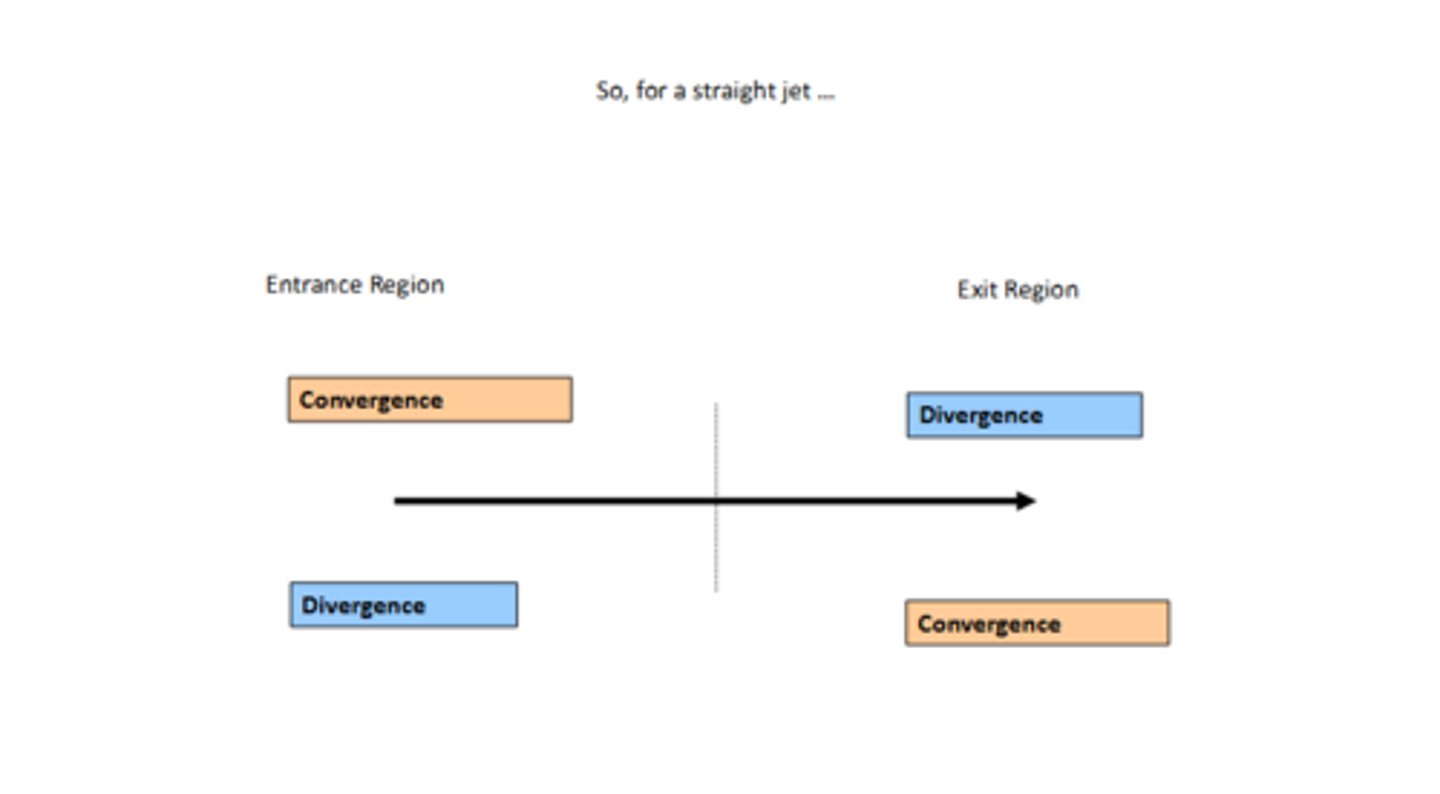
For a straight jet, if we look at the entrance region, where would we see convergence and divergence? Exit region?

Convergence in the LEFT entrance

Divergence in the RIGHT entrance

Divergence in the LEFT exit

Convergence in the right exit

If we are looking at a straight jet and are only considering ageostrophic motion, where would we see ageostrophic convergence and divergence?

Ageostrophic convergence in the left entrance and right exit

Ageostrophic divergence in the right entrance and left exit

Which direction does the meridional component of the ageostrophic wind point in the jet ENTRANCE? EXIT?

In the ENTRANCE, it points to the NORTH, while in the EXIT it points to the SOUTH.

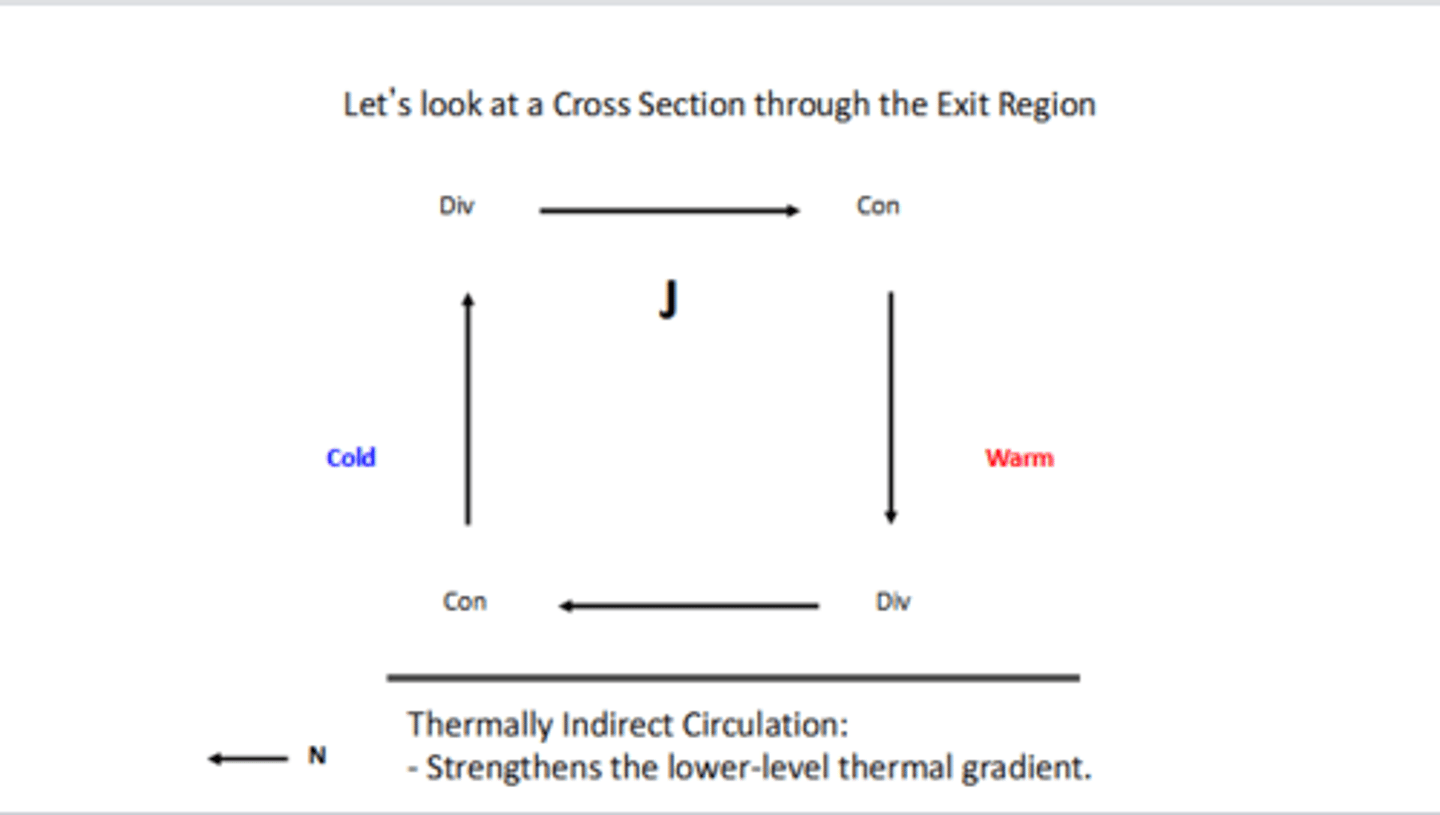
If you look at the cross-section through the EXIT region, do we see a thermally direct or indirect circulation, and what does it do to the lower-level thermal gradient?

We see a thermally INDIRECT circulation, and it would strengthen the lower-level thermal gradient

If you look at the cross-section through the ENTRANCE region, do we see a thermally direct or indirect circulation, and what does it do to the lower-level thermal gradient?

We see a thermally DIRECT circulation, and it would weaken the lower-level thermal gradient

Wind velocities decrease away from the jet streak. On the COLD side of the jet, do we see cyclonic shear vorticity or anticyclonic shear vorticity? On the WARM side?

On the cold side, we would see CYCLONIC shear vorticity

On the warm side, we would see ANTICYCLONIC shear vorticity

Looking at our different entrances and exits, where would we see AVA and CVA?

AVA: Left entrance and right exit

CVA: Right entrance and left exit

T or F: Downstream of the trough axis, the advection of anticyclonic vorticity yields increased convergence aloft and sinking motion. Similarly, upstream of the trough axis, the advection of cyclonic vorticity yields increased divergence aloft and rising motion.

False; Downstream of the trough axis, the advection of CYCLONIC vorticity yields increased DIVERGENCE aloft and RISING motion. Similarly, upstream of the trough axis, the advection of ANTICYCLONIC vorticity yields increased CONVERGENCE aloft and SINKING motion.

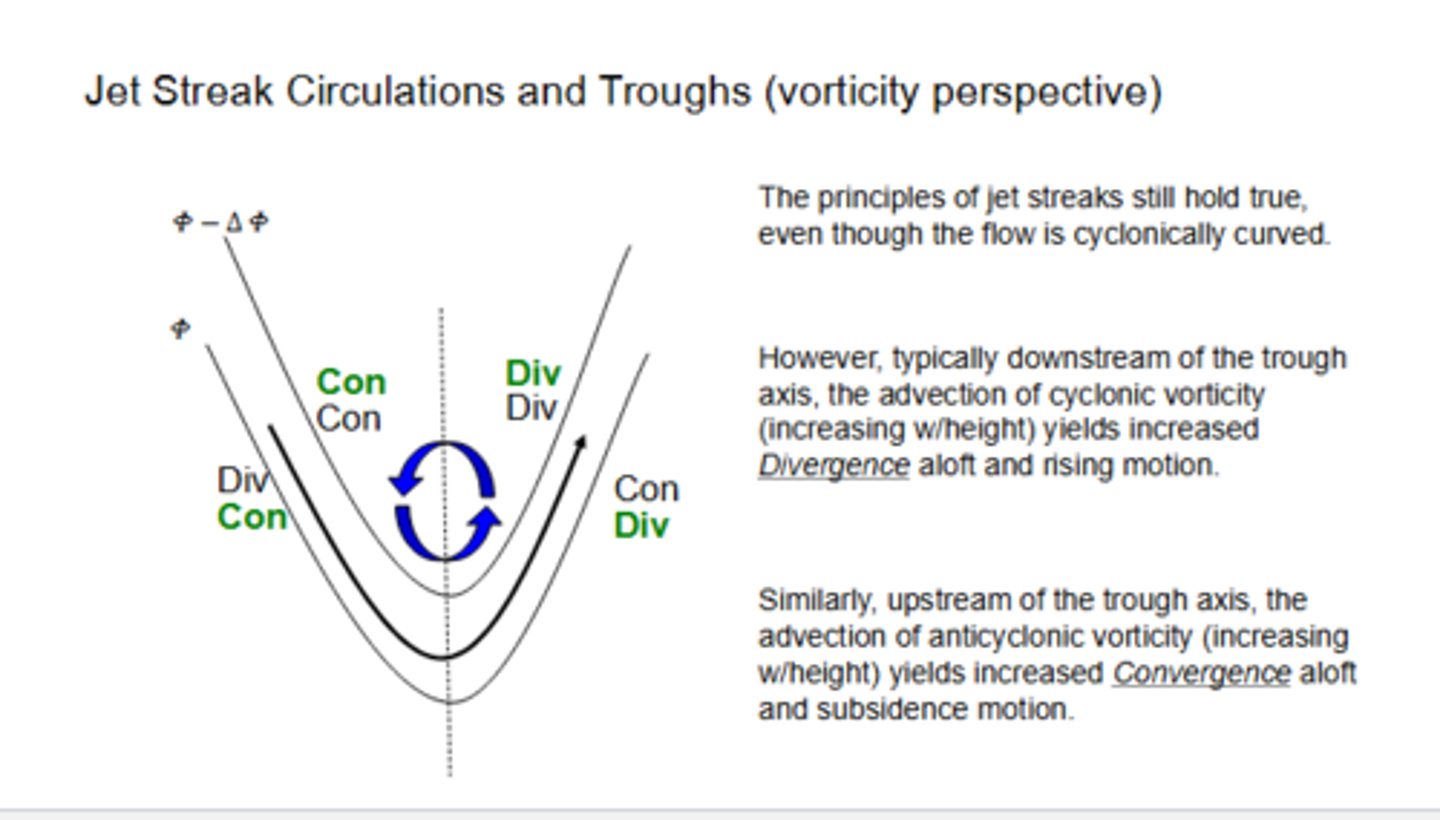
Where would we see enhanced divergence aloft occur in our jet streak in a trough? Enhanced convergence?

Enhanced divergence in the left EXIT region, enhanced convergence in the left ENTRANCE.

T or F: Downstream of the ridge axis, the advection of anticyclonic vorticity yields increased convergence aloft and sinking motion. Similarly, upstream of the ridge axis, the advection of cyclonic vorticity yields increased divergence aloft and rising motion.

True

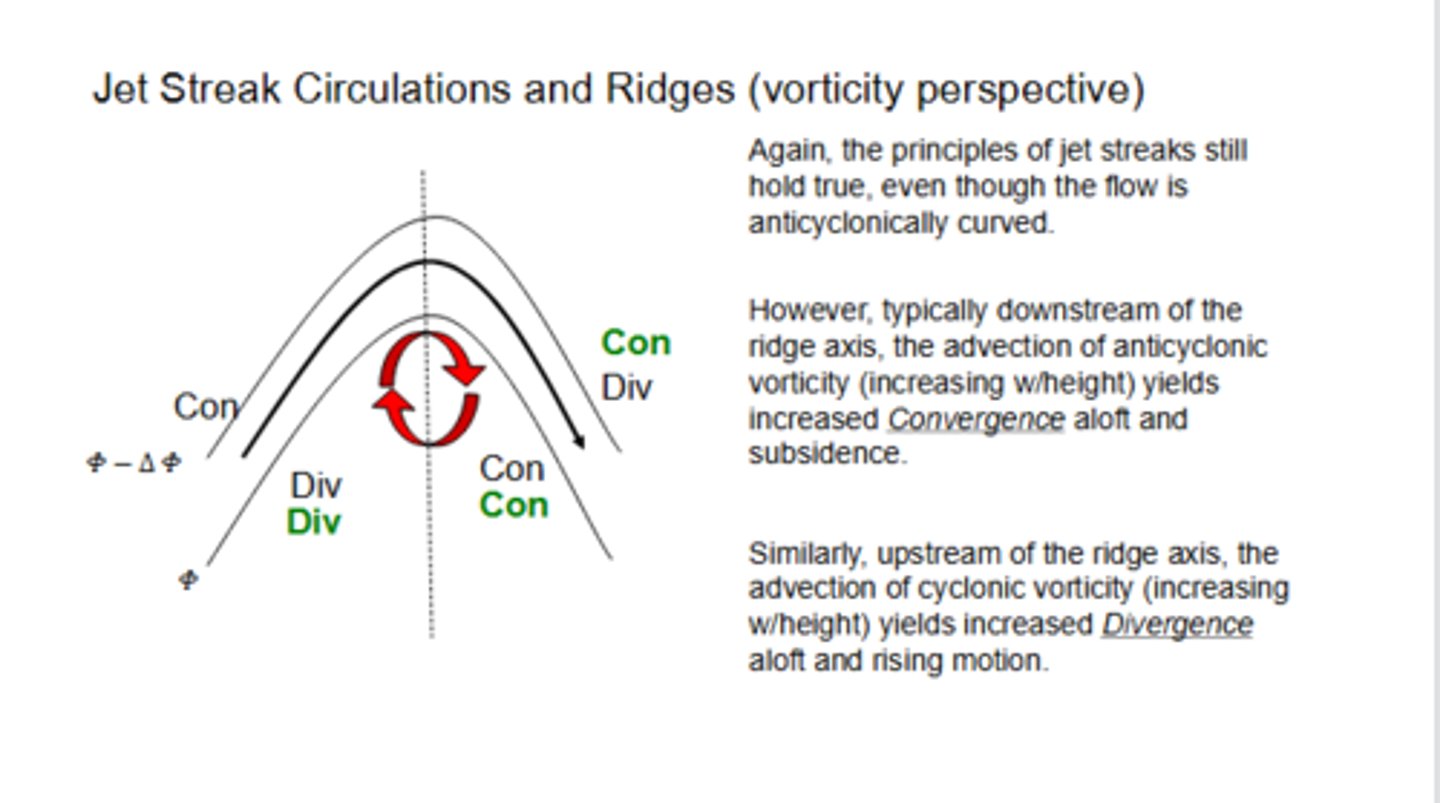
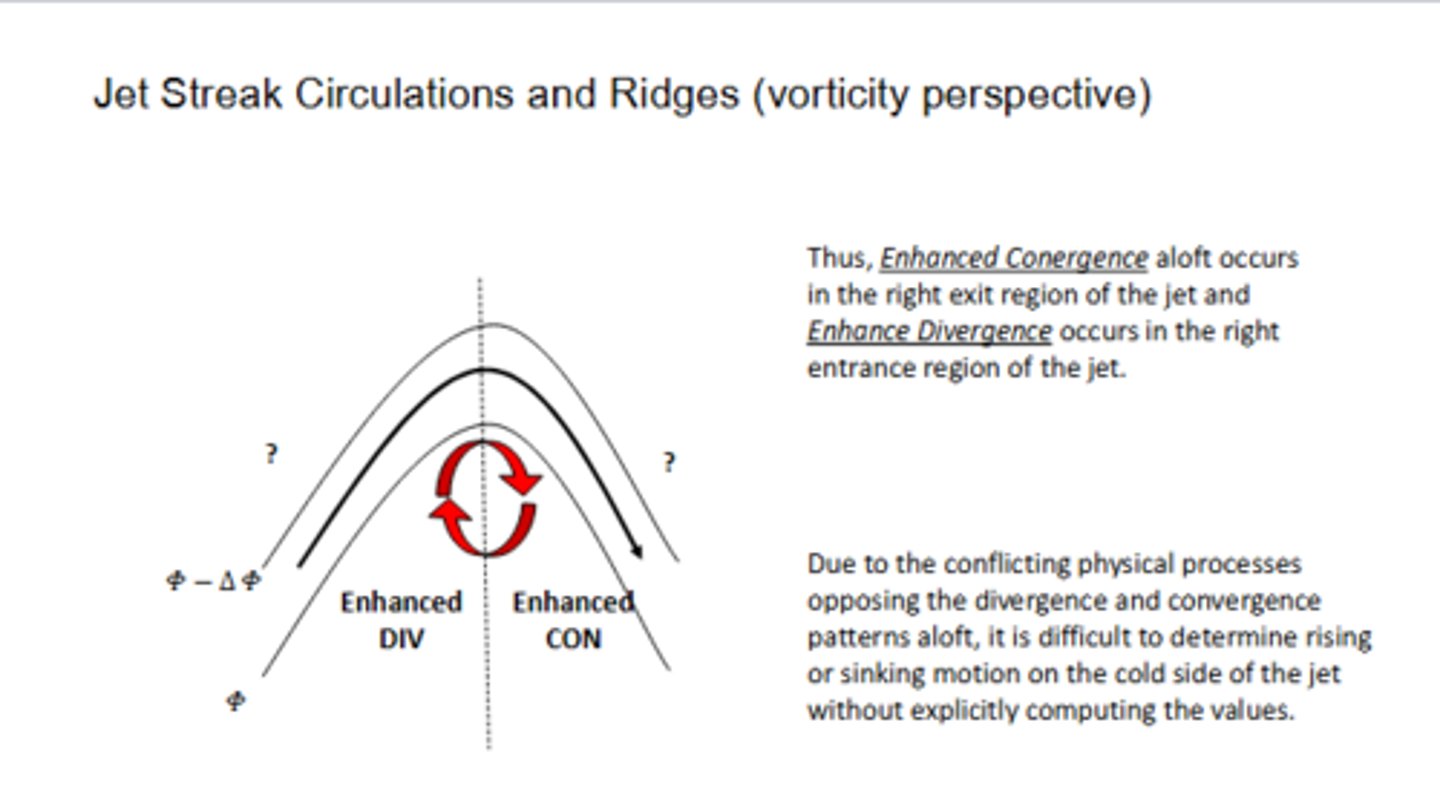
Where would we see enhanced divergence aloft occur in our jet streak in a ridge? Enhanced convergence?

Enhanced convergence aloft occurs in the right EXIT of the jet, and enhanced divergence occurs in the right ENTRANCE.

Week 9: QG Theory - Height Tendency

What does the QG height-tendency equation describe from a conceptual standpoint?

It illustrates processes leading to the development and movement of weather systems.

What are the 5 fundamental assumptions of the quasi-geostrophic approximation

1.) Small Rossby number ~ 0.1 (ageostrophic flow <10% of geostrophic flow)

2.) f = f0 + βy ("Beta plane" assumption)

3.) Frictionless flow ("optional")

4.) Adiabatic flow ("optional")

5.) Hydrostatic approximation

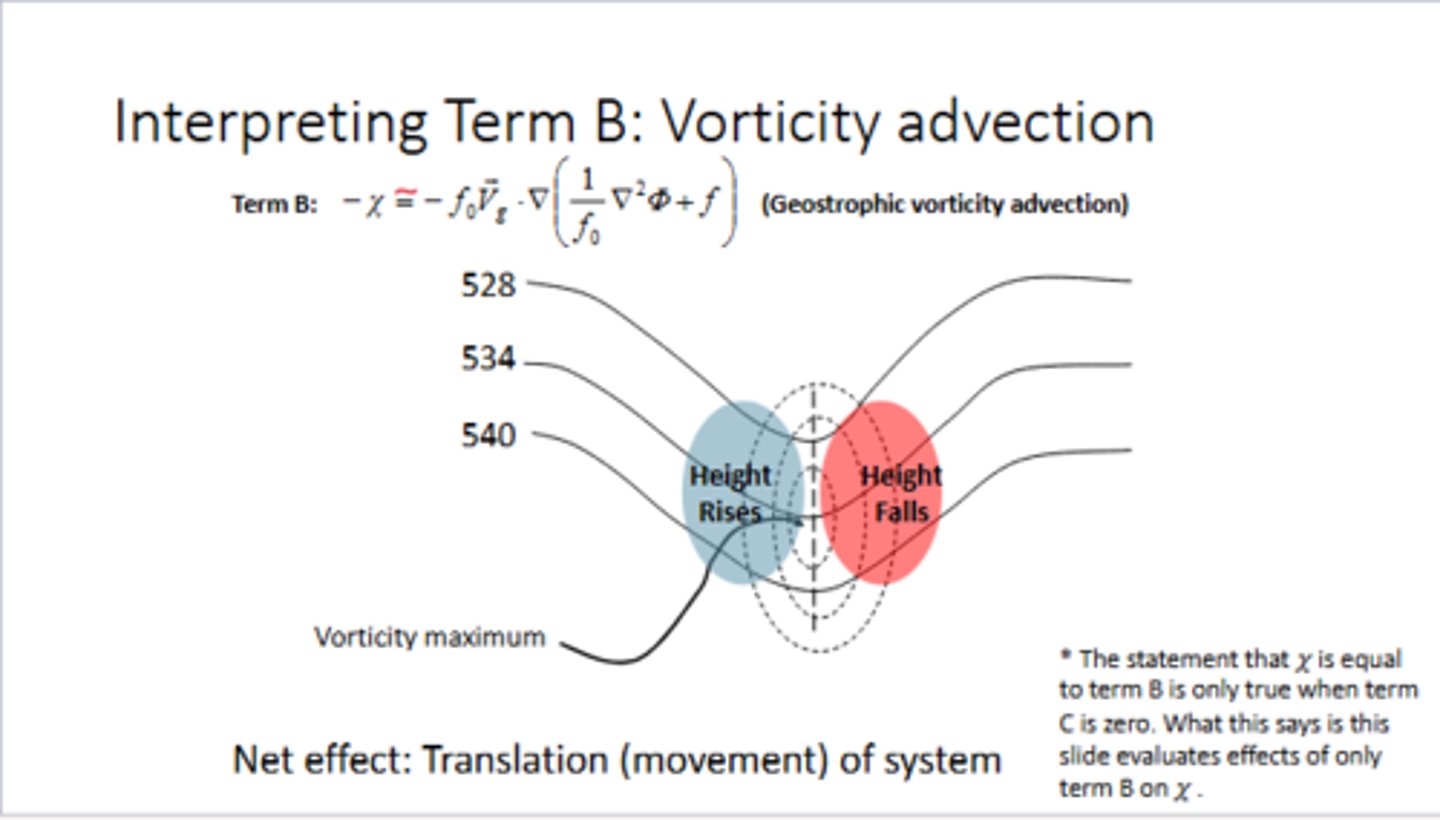
Looking at the QG height tendency equation, what do the three terms represent?

∇^2χ = f0 [Vg ⋅ ∇p(ζ + f) - f0^2/σ ∂/∂p[R/p(-Vg ⋅ ∇pT)]

Term 1 (LHS): The 3-D Laplacian of the height tendency

Term 2 (RHS): The absolute geostrophic vorticity advection by geostrophic wind (aka VA)

Term 3 (RHS): Differential thickness (temperature) advection by geostrophic wind (aka DTA)

Looking at a trough and its axis, where are you likely to see height FALLS? Height RISES?

EAST of a trough axis, you are likely to see height FALLS, while WEST of a trough axis, you are likely to see height RISES.

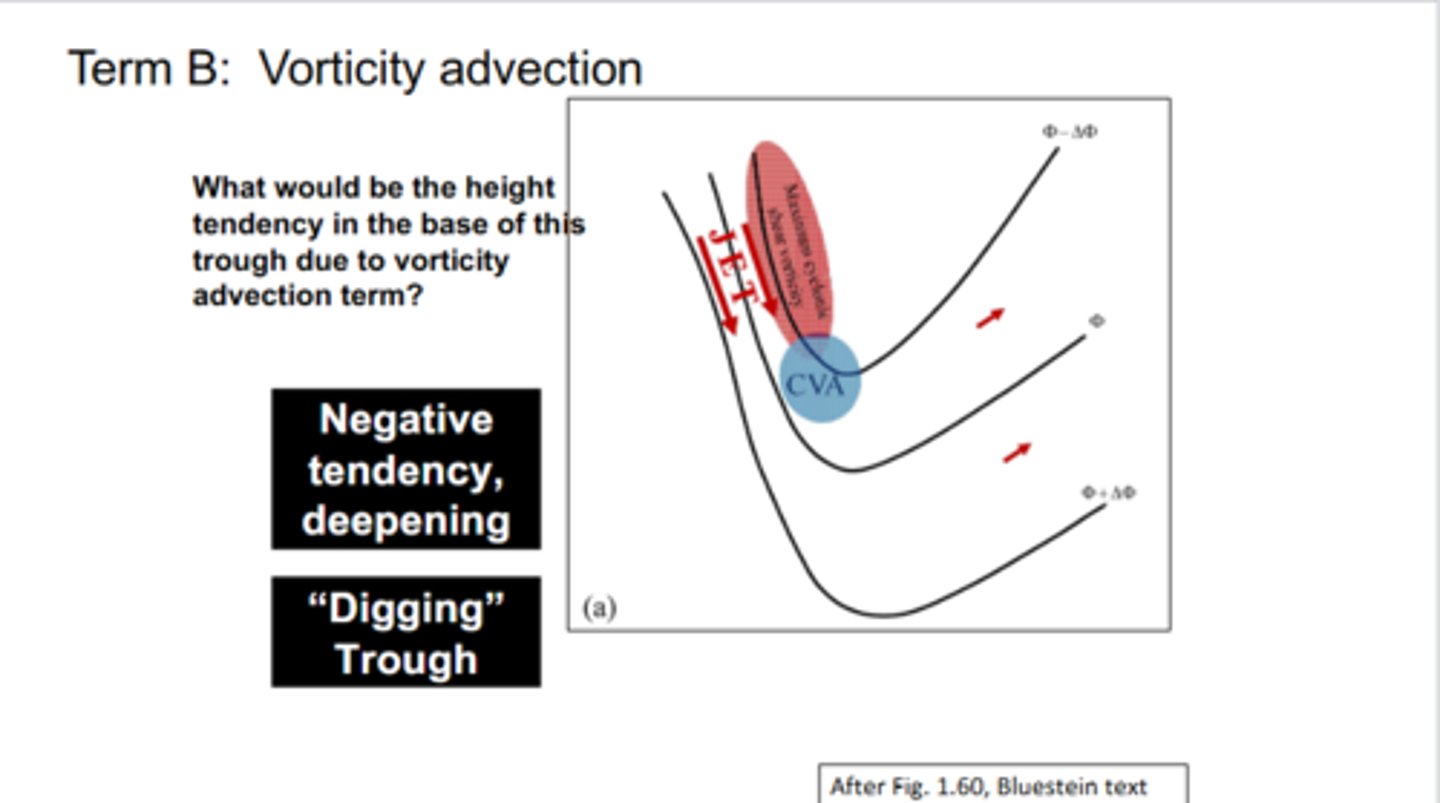
If you have your jet streak on the WEST side of your trough axis, what would be your height tendency to your vorticity advection term? What would this do to the trough

Since out ahead of your jet streak, you have CVA, which leads to a NEGATIVE height tendency. This leads to height falls or the trough begins to DIG.

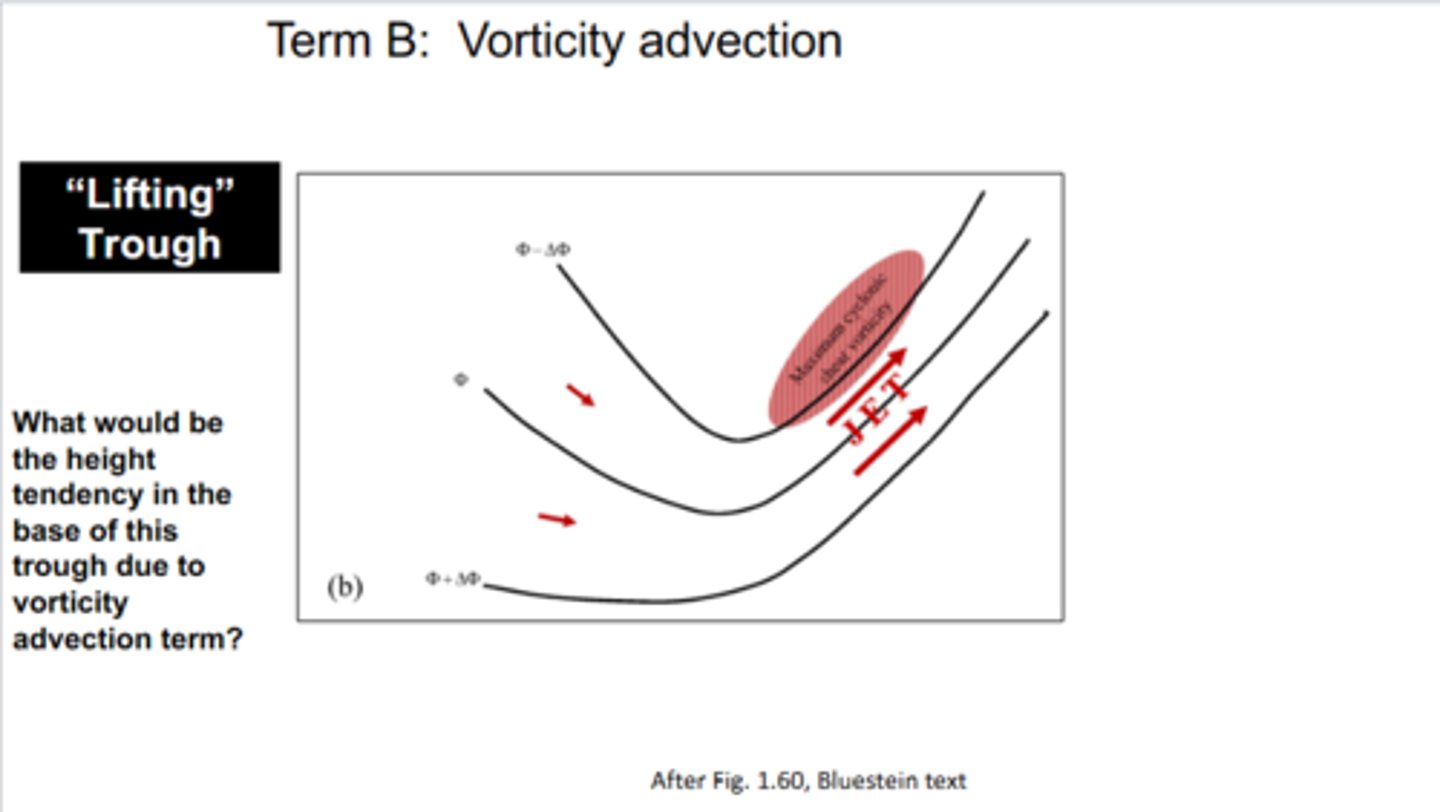
If you have your jet streak on the EAST side of your trough axis, what would be your height tendency to your vorticity advection term? What would this do to the trough

Your jet streak would exhibit AVA, which leads to POSITIVE height tendency. This leads to height rises or the trough begins to LIFT.

Looking at the DTA term in the equation, if we have a WARM advection maximum in between the sfc and 500 mb, what kind of height falls/rises would we expect at the sfc and 500 mb? Does it lead to the deepening of our trough or building of our ridge?

At 500 mb, we would see height RISES and height FALLS at the surface. This then leads to the BUILDING of our ridge.

Looking at the DTA term in the equation, if we have a COLD advection maximum in between the sfc and 500 mb, what kind of height falls/rises would we expect at the sfc and 500 mb? Does it lead to the deepening of our trough or building of our ridge?

At 500 mb, we would see height FALLS and heights RISES at the surface. This then leads to the DEEPENING of our trough.

Week 10: QG Theory - Omega

What does the QQ omega equation describe from a conceptual standpoint?

relates vertical air motion to thermal and vorticity advection

Looking at the QG omega equation, what do the three terms represent?

∇^2ω = -f0/σ ∂/∂p[-Vg ⋅ ∇p(ζg + f)] - R/σp∇^2p[-Vg ⋅ ∇pT]

Term 1 (LHS): 3-D Laplacian of the vertical motion

Term 2 (RHS): Differential absolute geostrophic vorticity advection by the geostrophic wind (aka DVA)

Term 3 (RHS): Laplacian of thickness (temperature) advection by the geostrophic wind

When looking at the QG omega equation, what sign should your terms be for the motion to be for RISING motion? SINKING motion?

RISING motion is forced by cyclonic vorticity advection (CVA), increasing with height, and WARM air advection.

SINKING motion is forced by anticyclonic vorticity advection (AVA), increasing with height, and cold air advection (CAA)