GRE Data

ways to present data

table, bar chart, segmented bar chart, histogram, pie chart, scatterplot, line graph

table (frequency distribution)

shows counts of observations in each category or interval. best for categorical data or grouped numerical data. example: apples (3), bananas (4), carrots (1)

table (relative frequency distribution)

shows proportion or percent in each category. best for comparing categories across different sample sizes. class frequency/total. example: apples (3), bananas (4), carrots (1) - apples = 3/8.

bar chart

shows frequency or percentage of categories.
data type: categorical (or discrete)
key feature: bars are separated
use when: comparing groups

segmented/stacked bar chart

shows: how a whole is divided into subcategories
data type: categorical & categorical
use when: comparing proportions within grfoups
example: gender breakdown within departments

histogram

shows: distribution of continuous numerical data
data type: quantitative, continuous
key feature: bars touch (because data is continuous)
use when: examining shape (skewness, symmetry, spread)
strength: reveals distribution patterns

pie chart

shows: parts of a whole
data type: categorical
use when: very few categories
weakness: bad for precise comparisons, sometimes misleading

scatterplot

shows: relationship between two numerical variables
data type: quantitative vs. quantitative

use when: looking for correlation, trends, outliers
strength: shows direction, form, and strength of relationships

line graph

shows: change over time or another ordered variable
data type: quantitative over an ordered sequence
use when: trends, growth, decline, seasonality
strength: best for time series data

what do measures of central tendency do?

indicate the “center” of the data

what are the measures of central tendency

mean, median, mode

weighted mean

number * frequency / total number

measures of position

where a value sits relative to the rest of the data

properties of median

resistant to outliers, depends on position, not magnitude)

quartiles

divide data into four equal parts q1 - 25th percentile, q2 - 50th percentile (median), q3 - 75th percentile

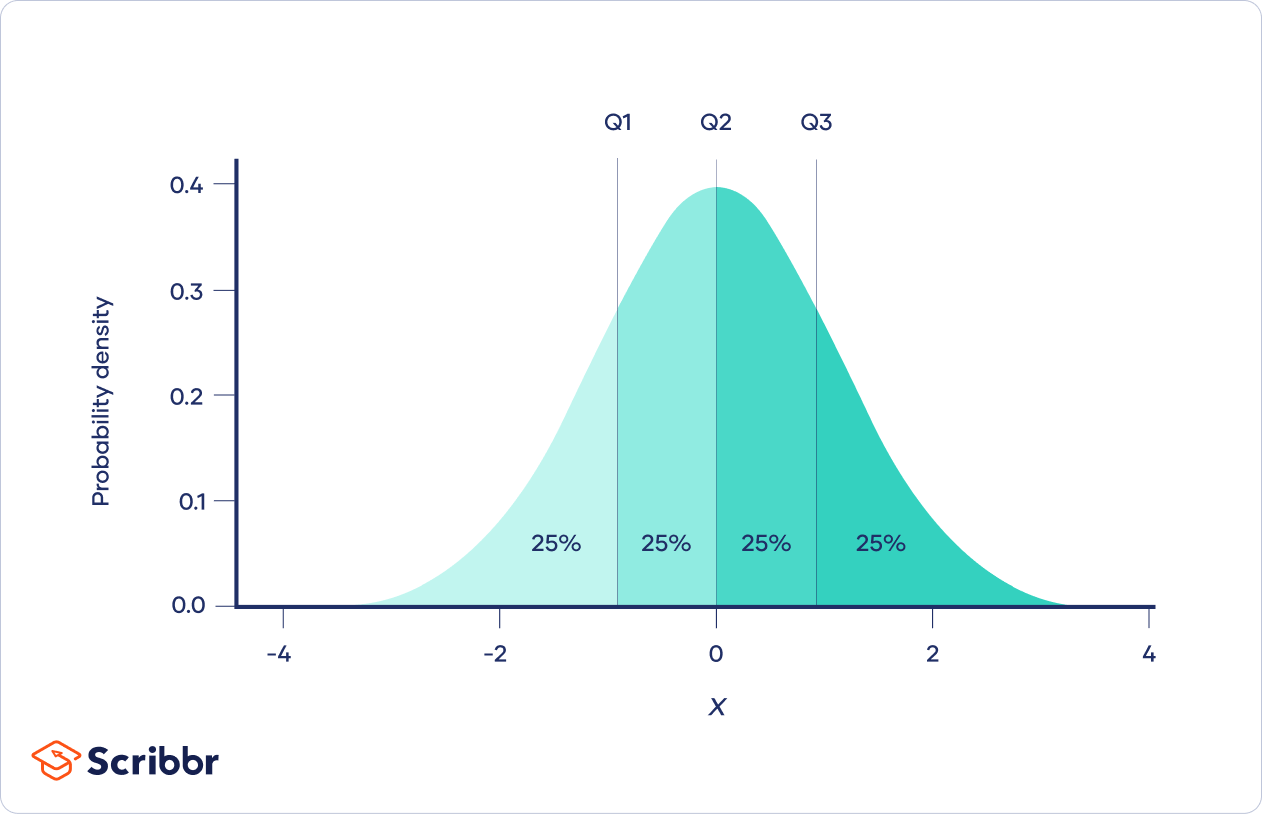
percentiles

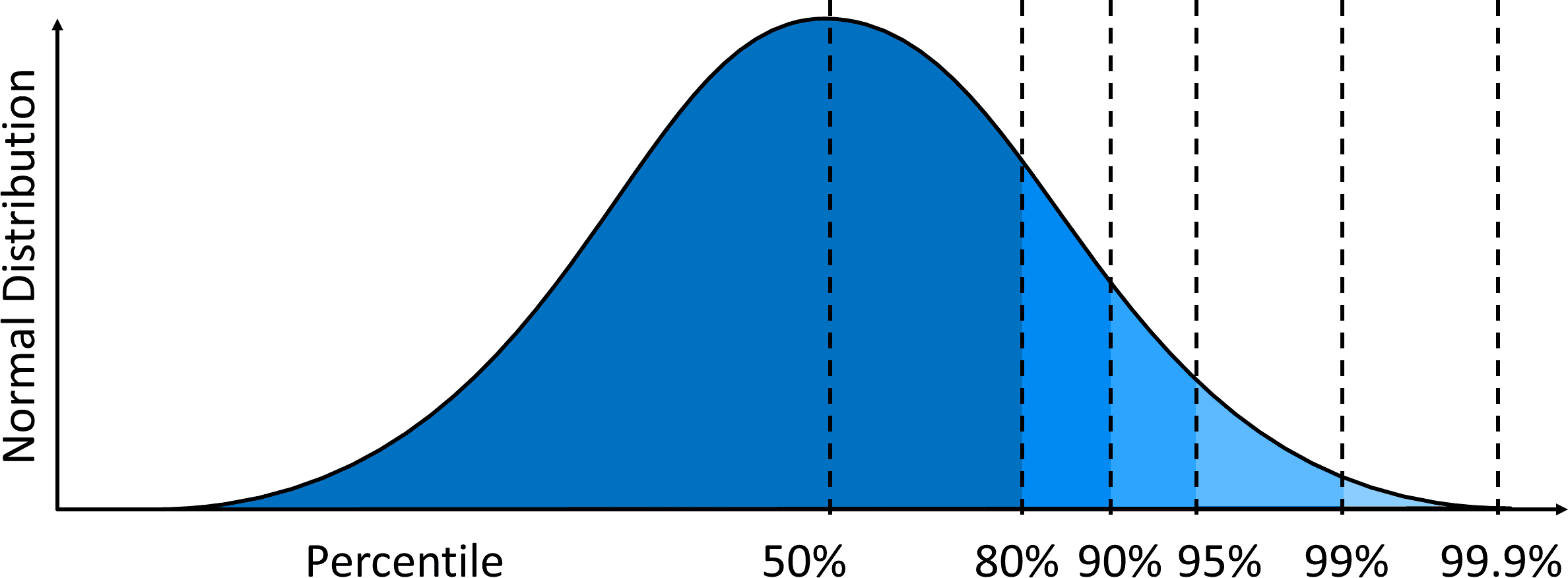
value’s relative standing in the data

90th percentile - higher than 90% of observations, 90% are below you

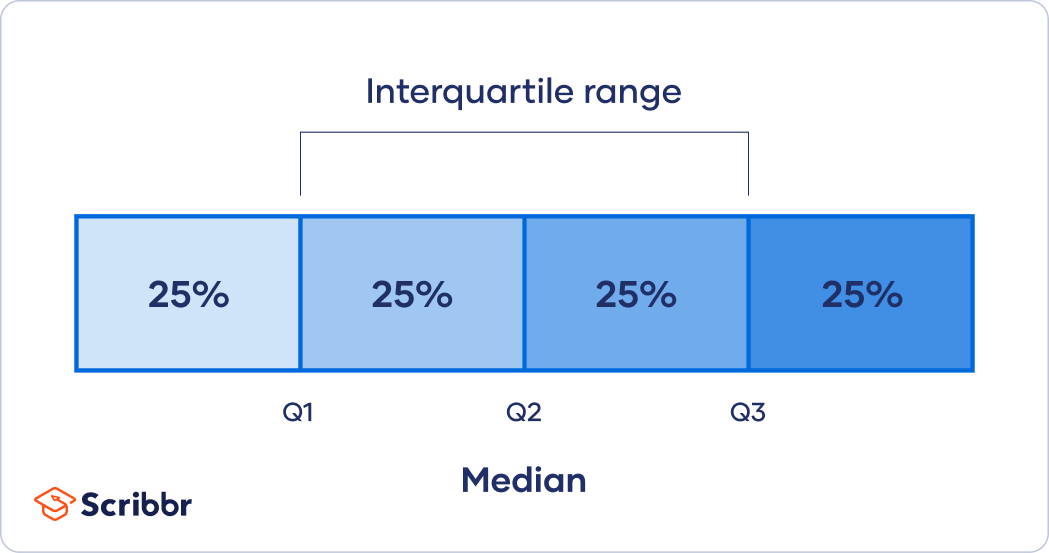
interquartile range

iqr = q3 - q1

measures spread of the middle 50%

resistant to outliers

measures of position

median, quartiles, percentiles, interquartile range, z-scores

not measures of position

mean, range, variance, standard deviation

what do measures of position let you do

compare distributions without raw data

reason about rankings

handle boxplots and percentiles logically

measures of dispersion

how spread the data is (4, 4, 4 = no spread; 1, 5, 6, 10, 20 = high spread)

range

large number and subtract the smallest number

range is always positive or 0

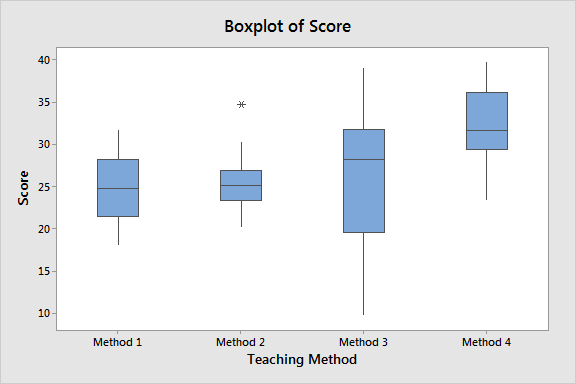
boxplot

shows aspects of data

number line + lowest #, q1, median, q3, highest number

then box the q1, median and q3

standard deviation

sense of spacing between numbers

how far they are from the meant

three scenarios of standard deviation

large: numbers are spaced out

small: numbers are close together

zero: numbers are all the same

what happens to the standard deviation when you add a number to every term?

no change

what happens to the standard deviation when you subtract a number from every term

what happens to the standard deviation when you

what happens to the standard deviation when you multiply a number

multiply the standard deviation by that number

what happens to the standard deviation when you divide a number

divide the standard deviation by that numberh

how to calculate the standard deviation

find the mean

subtract the mean from each value

square each deviation

find the mean of the deviations

take the square root