IB Physics HL: Kinematics

displacement (s)

change in position. It is the shortest distance of 2 points and is a vector quantity

in uniform motion this can be calculated by:

• s_i + vt

  • it gives the position of s of the moving object after t seconds where the initial position is s_i

distance (d)

The actual length of the path followed. It is a scalar quantity.

Velocity (v)

This is a vector quantity where in uniform motion, is calculated by the formulae:

• Δs/Δt (or will be seen as the average velocity in non uniform motion)

• s- s_i /Δt

when v is +ive then displacement is increasing, and vice verca

Average speed

calculated by total distance/total time. it is a scalar quantity

Uniform motion

Motion where velocity is constant

Instantaneous Velocity (v)

This is different to velocity as this is equal to the rate of change of position at a specific point of the motion and only matters in non-uniform motion. This means that v is the gradient of the line of a point on a position-time graph

acceleration (a)

This is a vector quantity defined as Δv/Δt when a is constant. When a isnt then this gives average acceleration. Hence, a is equal to the gradient of a velocity-time graph. If a is +ive, then velocity is increasing and vice verca

1st equation of motion

• a (constant) = Δv/Δt

• a = v-u / t

• v = u + at

The equations of motion only function if acceleration is constant

2nd equation of motion

The area under a velocity-time grave is the total displacement. the shape of a velocity time graph is a trapezoid, therefore the displacement can be calculated using the formula:

• Δs = ((u+v)/2) x t

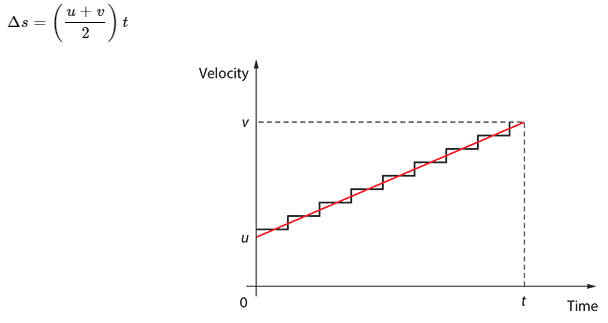
3rd equation of motion

v = u + at so therefore the equation s = ((u+v)/2) x t becomes…

• ((u+u+at)/2) x t

• s = ut + ½ at²

4th equation of motion

As v = u + at, t ∴ equals to (v-u)/a. Therefore causing the equation: s = ut + ½ at² to become…

• (v² - u² )/2a = s

• v² = u² + 2as

the equations of motion

1. v = u + at

2. Δs = ((u+v)/2) x t

3. s = ut + ½ at²

4. v² = u² + 2as

acceleration of free fall (g)

when an object is in free fall the variable “a” can be replaced by “g“ representing the downwards force of gravity. g is equal to 9.81 unless stated otherwise. Furthermore, the value of g will change to -g if the object is thrown vertically upwards, this is as the objects current velocity will be labeled as positive (eg. a ball is thrown upwards at 20m/s) and any vector force opposing that direction (i.e gravity, g) must be negative.

Projectile motion

This is where an object is moving along two planes at the same time. These planes are the x-direction and the y-direction. What happens in this situation is that the velocity that the object moves is split along the 2 vectors in the x and y directions respectively. This uses the Pythagorean theorem and hence, utilizes trigonometry. To resolve the vector use the following equations

• v_x = uCos θ

• v_y = uSin θ

Where v_x and v_y is the velocity in the x and y directions respectively.

The fact that the velocity is split means that all other variables (other than time) is also split between them. therefore each of the equations of motion must be edited to include the above edits.

Horizontal equations of motion applied to projectile motion

1. v = uCos θ

2. Δs = ((u+v)/2) x t

3. s = utCos θ

4. v² = u²Cos² θ

5. t = (2uSin θ)/g

Vertical equations of motion applied to projectile motion

1. v = uSin θ + gt

2. s = utSin θ - ½ gt²

3. v² = u²Sin²θ - 2gs

4. t = (2uSin θ)/g