IB Physics SL (Topic B)

Bidwell Boys, core concepts

Solids

• They have a fixed volume and do not flow.

• The particles are arranged in regular rows.

• The particles have relatively little energy and vibrate around fixed positions.

• The particles have relatively strong forces of attraction between them, called 

  intermolecular forces.

• When a solid is heated, the particles gain energy and move further apart, weakening the intermolecular forces.

• This results in the thermal expansion of the solid. For the same increase in temperature, a substance in its solid phase expands less than the same substance in its liquid and gaseous phases.

Liquids

• They can flow and take the shape of their container.

• The particles are arranged randomly.

• The particles have more energy than those in a solid of the same substance and can move around each other.

• The strength of the intermolecular forces is weaker than in a solid of the same substance, but stronger than in a gas of the same substance.

• When a liquid is heated, the particles gain energy and move further apart, weakening the intermolecular forces.

• This results in the thermal expansion of the liquid. For the same increase in temperature, a substance in its liquid phase expands more than the same substance in its solid phase but less than the substance in its gaseous phase.

Gases

• They can flow and fill their container completely.

• Their volume can change by altering the pressure and/or temperature.

• The particles are comparatively far apart and in a random arrangement.

• Compared to the solid and liquid states of the same substance, the particles have high amounts of energy and move quickly in all directions.

• For the same increase in temperature, a substance in its gaseous phase has the largest thermal expansion.

Internal Energy

The sum of intermolecular forces and intermolecular potential energies of the particles within a substance, contributing to its temperature (change in kinetic energy within substance) and phase (change in potential energy).

• solids = low kinetic energy and low potential energy

• gases = high kinetic energy and high potential energy

• intermolecular potential energy is negative because molecules tend to be attracted to each other. This means that, as the molecules get closer together, their potential energy decreases, and as they get further apart, their potential energy increases. Work must be done to bring molecules apart, work corresponds to increase in molecules’ potential energy. highest value of intermolecular potential energy is 0 which means the molecules have no interaction.

Temperature of gas vs. pressure, volume, and kinetic energy of molecules

When the temperature of a gas is decreased, the pressure and volume of the gas, and the kinetic energy of its molecules, will decrease towards zero. At this point, the temperature of the gas will be −273 °C.

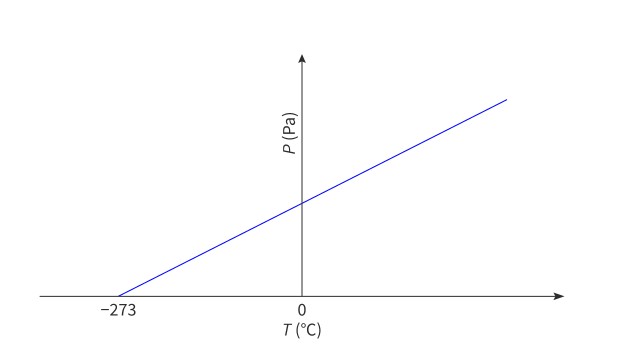
absolute zero

The lowest possible temperature (0 K) at which the pressure and volume of a gas are zero and the particles have zero kinetic energy.

Kelvin vs Celsius

As –273 °C is the same as 0 K, you can convert from °C to K by adding 273. 1K = 1°C

Kelvin and the average kinetic energy of molecules

Kinetic energy is proportional to temperature, (3/2)kB = slope of the average kinetic energy vs temperature graph in Kelvin.

• Ek = average kinetic energy of molecules (J)

• kB = Boltzmann constant (1.38 × 10⁻²³ J/K)

• T = absolute temperature (L)

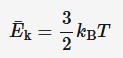
Specific heat capacity

The amount of energy required to increase the temperature of 1 kg of a substance by 1 °C. Also can be thought of as the amount of energy released by 1kg of a substance when its temperature decreases by 1K.It is a measure of a substance's ability to store thermal energy.

• m = mass of substance to be heated (kg)

• c = specific heat capacity (J*kg^-1*K^-1)

• Δ⁢T = change in temperature (°C or K)

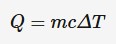
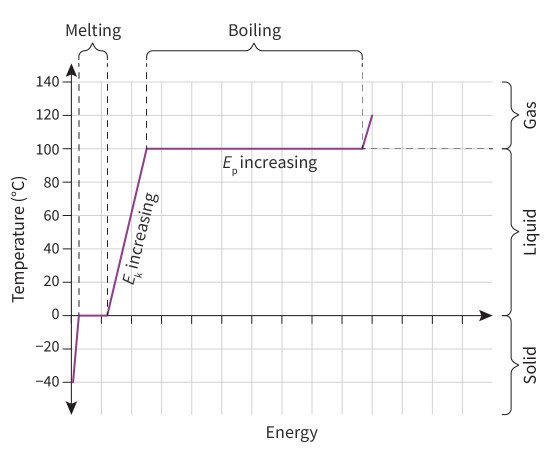
Phase Change

• When a substance remains in the same phase and is heated, the energy supplied is transferred to the kinetic energy of the particles, thus increasing the temperature of the substance.

• During a change of phase, all of the energy supplied is transferred to the potential energy of the particles and not kinetic energy. For this reason, all of the energy supplied provides the particles with more energy to overcome the intermolecular forces of attraction between them. This allows them to move further apart, and the volume of the substance expands. For this reason, during a change of phase, the temperature of the substance remains constant.

Specific latent heat

The amount of energy required to change the phase of 1 kg of a substance at constant temperature.

• During a phase change, the equation for specific heat capacity does not apply, as there is no change in temperature.

• specific latent heat of fusion = solid to liquid

• specific latent heat of vaporization = liquid to gas

• Q = energy (J)

• m = mass of substance heated (kg)

• L = specific latent heat of fusion or vaporization (J*kg^-1)
  

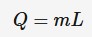
thermal equilibrium

The process of heat moving from one area to another until both areas are balanced with the same amount of thermal radiation. Goes from hot to cold always.

Conduction

The transfer of thermal energy due to collisions between particles that are in direct contact with each other.

• Thermal energy is supplied to one part of the solid.

• This energy is transferred to the kinetic energy of the particles closest to the heat source, and they start to vibrate more.

• They collide with neighbouring particles, transferring energy to them.

• When thermal equilibrium is reached, the net energy transfer is zero.

• best conductors are metals

• soilds are better conductors as particles are close together

rate of thermal energy transfer by conduction/ Fourier’s conduction laws

The amount of energy transferred per unit time,

• Fourier’s conduction law states that the rate at which thermal energy is transferred from one side of a material to the other depends on the thermal conductivity of a material, its cross-sectional area, and the difference in temperature between the hot part of the material and the cooler part of the material (known as the temperature gradient).

• The reason that metals are good thermal conductors is because of the free electrons because kinetic energy is also transferred to the electrons

• ΔQ/Δt = rate of thermal energy transfer

• ΔT/Δx = temperature gradient

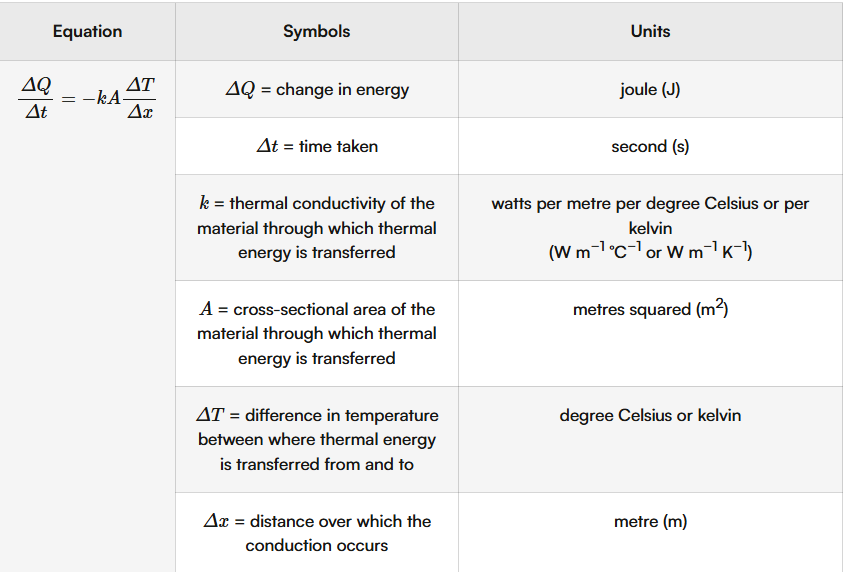
Convection

The transfer of thermal energy due to the mass movement of molecules. Occurs best in liquids and gasses as molecules can move freely

• Thermal energy is supplied to one part of the fluid.

• This energy is transferred to the kinetic energy of the particles closest to the heat source, and they start to move faster.

• They collide with neighbouring particles more energetically, so the particles spread further apart.

• This part of the fluid is now less dense and therefore rises. A cooler, denser, volume of particles moves into the space.

• This process repeats in a continuous cycle known as a convection current.

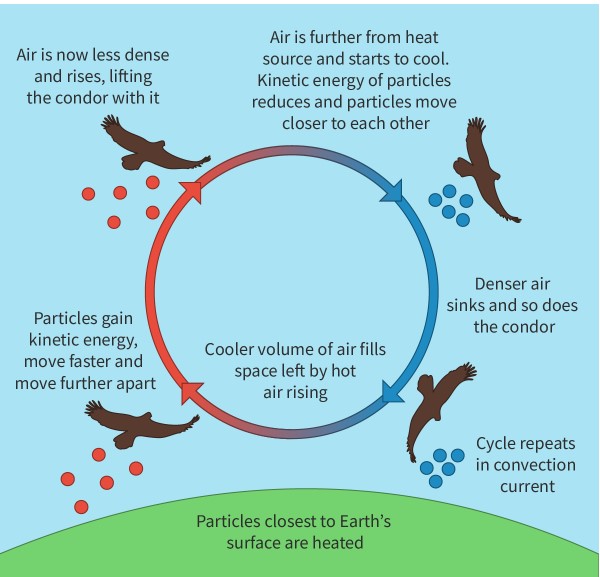
Thermal radiation

Transfer of energy by electromagnetic waves. Does not need particles to travel and can transfer energy through a vacuum. All objects with >0 kelvin emit thermal radiation, greater the temperature = higher intensity of thermal radiation.

• the properties of a material affect how effective it is at absorbing, emitting, or reflecting thermal radiation

Intensity

the amount of power incident on one square metre of the surface of an object.

• with a spherical light source (like a star) the equation is I = P / (4πr²)

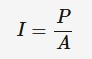
Black bodies

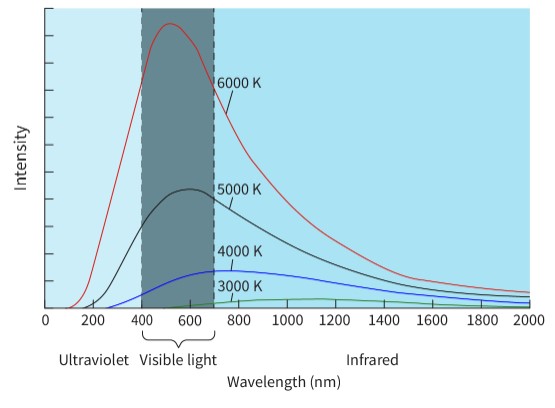
An object that absorbs all the energy of all the wavelengths of electromagnetic spectrum that are incident upon it. Once the object is in equilibrium, it will emit all wavelengths of the electromagnetic spectrum.

• It shows that some radiation is emitted at all wavelengths.

• It has a maximum intensity at a specific wavelength.

• It is not symmetrical – it rises steeply then drops off less steeply after the peak and approaches the x-axis as an asymptote.

• It does not pass through the origin.

• The shape of these graphs and the peak wavelength are not dependent on the material. The only thing that affects the peak wavelength is the temperature of the black body. This peak value can be used to determine the temperature of any black body.

Wien’s law

Wien’s law states that the wavelength at which the maximum intensity of radiation is emitted is related to the absolute temperature of a black body by the equation:

• λmax = wavelength at which maximum
  intensity is emitted (m)

• T = absolute temperature (K)

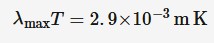
Luminosity

The amount of energy a black body emits per second. Measured in watts (W).

• can also be expressed as L_☉, which compares luminosity to the luminosity of the sun, Betelgeuse is 150000 more luminous than the sun therefore it is 150000L_☉.

Stefan-Boltzmann law

This law is used to calculate luminosity, Stefan-Boltzmann law tells us that the luminosity is directly proportional to the area of a star and also directly proportional to its absolute temperature, raised to the power 4.

• o = Stefan-Boltzmann constant

• A = surface area of sphere (4*pi*r²)(m²)

• T = absolute temperature (K)

• we can also say that the luminosity of a star is directly proportional to its radius squared.

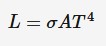
Apparent brightness

A measure of how bright a star appears. It is measured by the amount of energy received per square metre per second by an observer on Earth. Also known as apparent magnitude. Luminosity is a property of the star, apparent brightness depends on intensity of light received by observer

• L = luminosity (watt)

• d = distance between the emitter and the observer (m)

• b = apparent brightness (W*m^-2)

• This equation tells us that the brightness of a star is directly proportional to its luminosity and inversely proportional to the square of its distance from the observer.

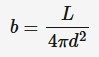
Thermal Equilibrium

The process of heat moving from one area to another until both areas are balanced with the same amount of thermal radiation.

emissivity

A measure of the effectiveness of a surface to emitting thermal radiation. It is the ratio of the energy radiated by an object compared to the energy emitted by a black body per unit area at the same temperature and wavelength of radiation. Good emitters are also good absorbers. Max value is 1 meaning it is a perfect black body.

• come back to add picture

• o = Stefan-Boltzmann constant

• T = absolute temperature

macroscopic system

The objects in a macroscopic system can be seen with the unaided eye.

Albedo

A measure of the fraction of solar radiation that is reflected off a macroscopic system compared to the total incident radiation. Max value for albedo is 1.

• add pic later

Solar constant

A measure of the amount of solar electromagnetic radiation reaching the Earth's outer atmosphere per unit area per second. Its value is equal to the average apparent brightness of the Sun from Earth.

• TO calculate the amount of energy incident on 1m² of the surface of the Earth’s atmosphere in 1 second.

• A = 4*pi*r² = 2.827 × 10^23

• Sun emits 3.9 × 10^26 J, to determine the amount of energy incident on 1m² we must divide this energy by the surface area of the sphere over which the Sun’s energy is distributed

• value of solar constant is given in physics data booklet, 1.36 × 10³ W*m^-2

• average amount of energy incident per second per metre squared on the surface of the Earth S/4

The greenhouse effect

if the earth acted as a black body with no atmosphere the average temp would be -20C. However due to gases in the atmosphere that absorb infrared radiation directly from the Sun and from the surface of the Earth. Main greenhouse gases are carbon dioxide, methane, nitrous oxide and water vapour. These gas particles re-emit this energy in all directions, some energy into space and some back toward Earth trapping it in the Earth-atmosphere system.

enhanced greenhouse effect

Natural variations and human activity have increased the concentration of greenhouse gases in the atmosphere, thus absorbing more thermal radiation in the Earth surface–atmosphere system.

• The greenhouse gases that do absorb infrared radiation are carbon dioxide (CO₂), methane (CH₄), nitrous oxide (N₂O) and water vapour (H₂O).

Why do some gases absorb radiation while others do not?

Gases absorb radiation based on their molecular structure and the ability to vibrate at specific frequencies. If the incident radiation has a frequency equal to that of the molecules’ natural frequency of vibration, the molecules absorb the energy and resonance occurs. This means that the amplitude of vibration of the molecules is maximum. The natural frequency of vibration of the greenhouse gases is within the range of frequencies of infrared radiation. So the greenhouse gases absorb this radiation.

Light can exist as a wave and as a particle, called a photon, which has a specific amount of energy depending on the frequency of the light. Molecules can be interpreted to have discrete energy levels and they can only exist at these set energy levels. The exact molecular energy levels available are dependent on factors beyond the scope of the DP physics curriculum. If a photon energy matches the gap between molecular energy levels the photon will be absorbed and the molecule increases its energy. At some later point in time, the molecule will drop back down an energy level and re-emit the photon in a random direction.

microscopic systems

The objects in a microscopic system cannot be seen with the unaided eye.

pressure

which is the force applied per unit area in a direction 

perpendicular to the surface over which it is applied. Measured in newton per metre squared or pascals.

• F - force exerted perpendicular to the surface (N)

• A - area over which the force is distributed (m²)

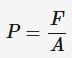
ideal gas

a gas in which

• there is a very large number of particles, which allows statistical averages to be taken

• the volume of each particle is negligible (small enough to be ignored) compared to the volume of the container

• there are no intermolecular forces between the particles

• the particles move randomly in all directions at high speeds

• collisions between particles and between particles and the walls of the container are perfectly elastic – kinetic energy is conserved

• the duration of a collision is negligible compared to the time between collisions

• the potential energy between particles is zero.

  An ideal gas is a model designed to approximate a real gas. We use the ideal gas model to make predictions about the behaviour of the molecules of a real gas. Ideal gases do not exist but are good approximations of real gases when the real gas:

  • is at a high temperature (so the speed of the particles is high and the duration of collisions is short)

  • is at a low pressure

  • is at a low density (so that the volume of the particles is negligible compared to that of the whole gas).

Moles

6.02 × 10^(23), is an SI unity for amount of substance and it has symbol n

• N = number of molecules

• NA = Avogadro constant

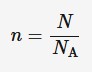
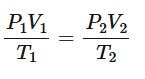
Ideal gas laws

1. The first gas law, also known as Boyle’s law states that for a constant mass of gas at constant temperature, the pressure of the gas is inversely proportional to its volume.

2. The second law, often known as Charles’ law, states that, for a constant mass of gas at constant pressure, the volume of the gas is directly proportional to its temperature in kelvin.

3. The third law, which is also called the pressure law, states that, for a constant mass of gas at constant volume, the pressure of the gas is directly proportional to its temperature in kelvin.

   • P = pressure (Pa)

   • V = volume (m³)

   • T = absolute temperature (K)

   • n = amount of substance (mol)

   • R = gas constant

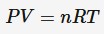
equation for gas pressure but with number of particles instead of moles

• P = pressure (Pa)

• V = volume (m³)

• T = absolute temperature (K)

• N = number of particles

• kB = Boltzmann constant

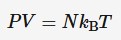
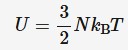
Internal energy of ideal gases

Because there is no intermolecular forces between particles in an ideal gas, all of the internal energy must by kinetic. Internal energy is based on temperature but joules and temp are not even so we must use a physical constant to convert between the two. It being (3/2)kB

• N = number of particles

• kB = Boltzmann constant

• T = absolute temperature (K)

• n = amount of substance (mol)

• R = gas constant

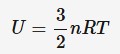
ideal gases and gas pressure

When a particle collides with the wall of its container, it bounces back with the same speed but different direction. This is a change in velocity and there is a force exerted on the wall, resulting in pressure.

• p = density (kg*m^-3)

• v = average velocity of particles (m*s^-1)

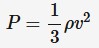
electromotive force (emf)

The amount of energy transferred to each unit of charge. Measured in volts

Electric potential difference

The work done per unit charge on moving a positive charge between two points along the path of the current.

• W = work done (J)

• q = charge (Coulombs)

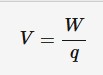
Coulomb

One coulomb is the amount of charge on 6.25 × 10¹⁸ electrons.

Electric current

The rate of flow of charge carriers. Measured in amperes (amps). Direct current can be calculated with the following.

• Δq = charge (C)

• Δt = time (s)

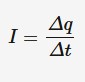
resistance

A measure of how difficult current can pass through an electrical component. It is harder for a current to pass through a component with high resistance than one with low resistance. Measured in ohms

• V = electric potential difference (V)

• I = current (A)

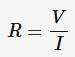
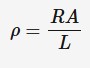
Resistivity

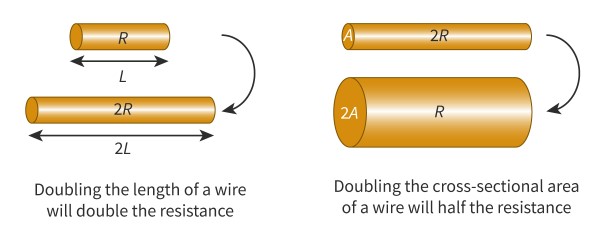
The property of a material that measures how strongly it resists current. The resistance of an electrical component (such as a wire) depends on its resistivity, length and cross-sectional area.

• p = resistivity (ohm * meters)

• R = resistance (ohms)

• A = cross- sectional area (m²)

• L = length (m)

Ohm’s law

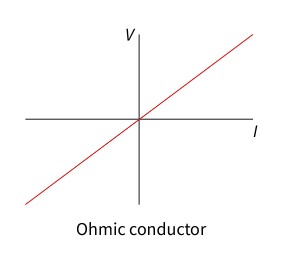
The electric potential difference across a conductor is directly proportional to the current flowing through it, at constant temperature.

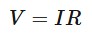
ohmic conductor

The electric potential difference across it per unit current (resistance) is constant.

• does follow Ohm’s law

non-ohmic conductors

The electric potential difference across it per unit current (resistance) is not constant.

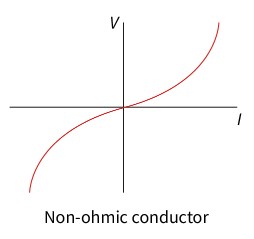
resistance and temperature

As current flows through an electrical conductor, such as a wire, some of the electrons collide with the lattice of metal ions. Some of the kinetic energy of the electrons is transferred to the ions as thermal energy via inelastic collisions (subtopic A.2). This raises the temperature of the wire.

As the temperature increases, the ions in the lattice vibrate faster, increasing the chance of collisions between the electrons and the lattice. This impedes the flow of the electrons, which means the resistance increases.

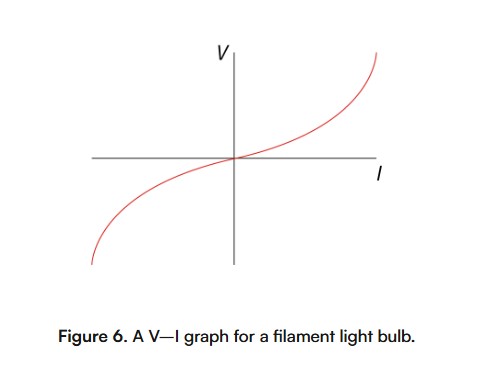
If the resistance of an electrical conductor changes with temperature, then it is a non-ohmic conductor. A filament light bulb is an example of a non-ohmic conductor. It consists of a wire enclosed in a partial vacuum by glass.D

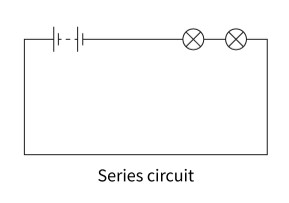
Series circuit

In a series circuit, all the components are in one loop of wire, and the same current flows through them all. Ammeters are connected in series with the other components in a circuit.

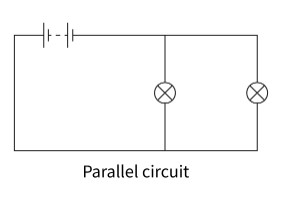
parallel circuit

When components are connected in parallel, the circuit has different branches for the current to go through. The current splits when it comes to a junction, and rejoins before returning to the cell or battery. In a parallel circuit, the potential difference across each branch of the circuit is the same.

Parallel vs Series circutis

Series circuits

• amperage, I total = I1 = I2 = I3 = …

• voltage, V total = V1 + V2 + V3 + …

• resistance, R total = R1 + R2 + R3 + …

Parallel circuit

• amperage, I total = I1 + I2 + I3 + …

• voltage, V total = V1 = V2 = V3 = …

• resistance, 1/R total = 1/R1 + 1/R2 + 1/R3 + …

voltmeter vs ammeter

To measure the current passing through a component, an ammeter is placed in series with the component. If the ammeter has a resistance, there is an electric potential difference (because V = IR) across the ammeter itself. This decreases the electric potential difference across the component. Therefore, ammeters are manufactured with a minimal resistance.

A voltmeter is placed in parallel with a component to measure the electric potential difference across it. If the voltmeter has a low resistance, a non-negligible current is drawn by the voltmeter. This increases the total current from the power source. Therefore, voltmeters are manufactured with a large resistance.

An ideal ammeter has zero resistance, while an ideal voltmeter has infinite resistance.

internal resistance

The resistance inside a cell that causes the electric potential difference across a cell to be less than its emf when the cell is in series with a resistor. This is because the conductive components and the store of chemical energy have resistance.

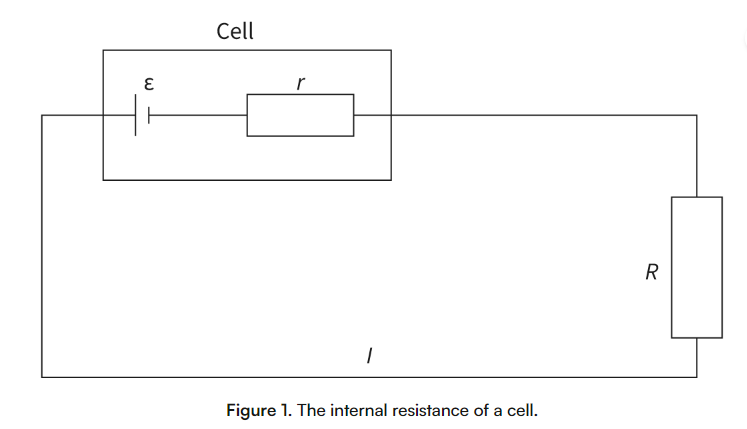
Total resistance of a circuit

The total resistance of the circuit is r+R.

Using Ohm’s law:

                V = I⁢R

                ε = I*(r+R)

• ε = emf of the cell (V)

• R = resistance of the circuit (ohms)

• I = current flowing through the circuit (A)

• r = internal resistance (ohms)
  

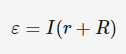
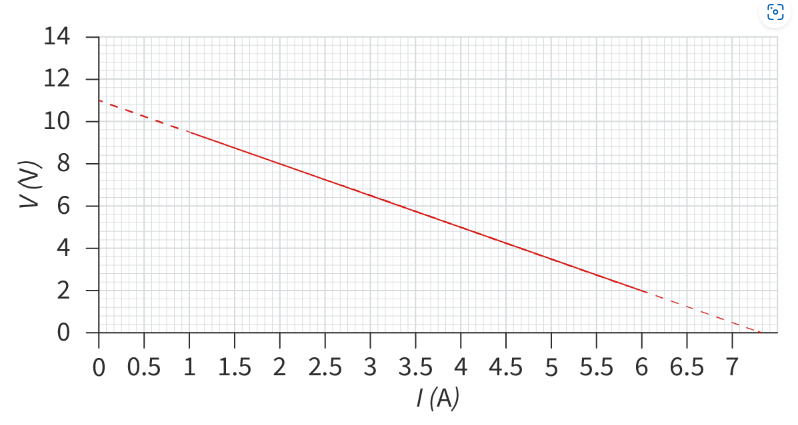
Interpreting a V–I graph to find emf and internal resistance

We can set up a circuit with a variable resistor to obtain multiple readings of electric potential difference and current. If we plot a graph of electric potential difference against current, we can use it to determine the emf and internal resistance of a cell. A potentiometer is an example of a variable resistor.

•  ε = I*(r + R)

•  ε = Ir + IR

•  ε = Ir + V

• V = -Ir +  ε, where the gradient is the internal resistance and the y-intercept is the emf.

Why does it appear to have no internal resistance when a voltmeter is connected across a cell?

An ideal voltmeter has infinite resistance. When it is connected across a cell, the current is 0A. Rearranging ε = I*(R + r) we can get V = ε - I*r, and because there is no current V = ε. Therefore, it appears that the cell has no internal resistance.