Linear Algebra Prelim 1 Study Guide

Linearly Independent Condition

i) the columns of matrix A are linearly independent

ii) see image

iii) there is a pivot in every column of A

Linear Independence of Two Vectors

*does not generalize to 3 vectors, if subsets of 2 are linearly independent the set of 3 vectors can still be dependent

Connection Between Linear Independence and Linear Combination Theorem

T/F If S is a linearly dependent set, then each vector is a linear combination of the other vectors in S

False, it guarantees some vector is, not each vector

T/F If a set contains fewer vectors than there are entries in the vectors, then the set is linearly independent.

False, it could be linearly dependent

(T/F) The columns of any 4 x 5 matrix are linearly dependent.

True, five vectors in R4 must be linearly dependent.

domain, codomain of transformation

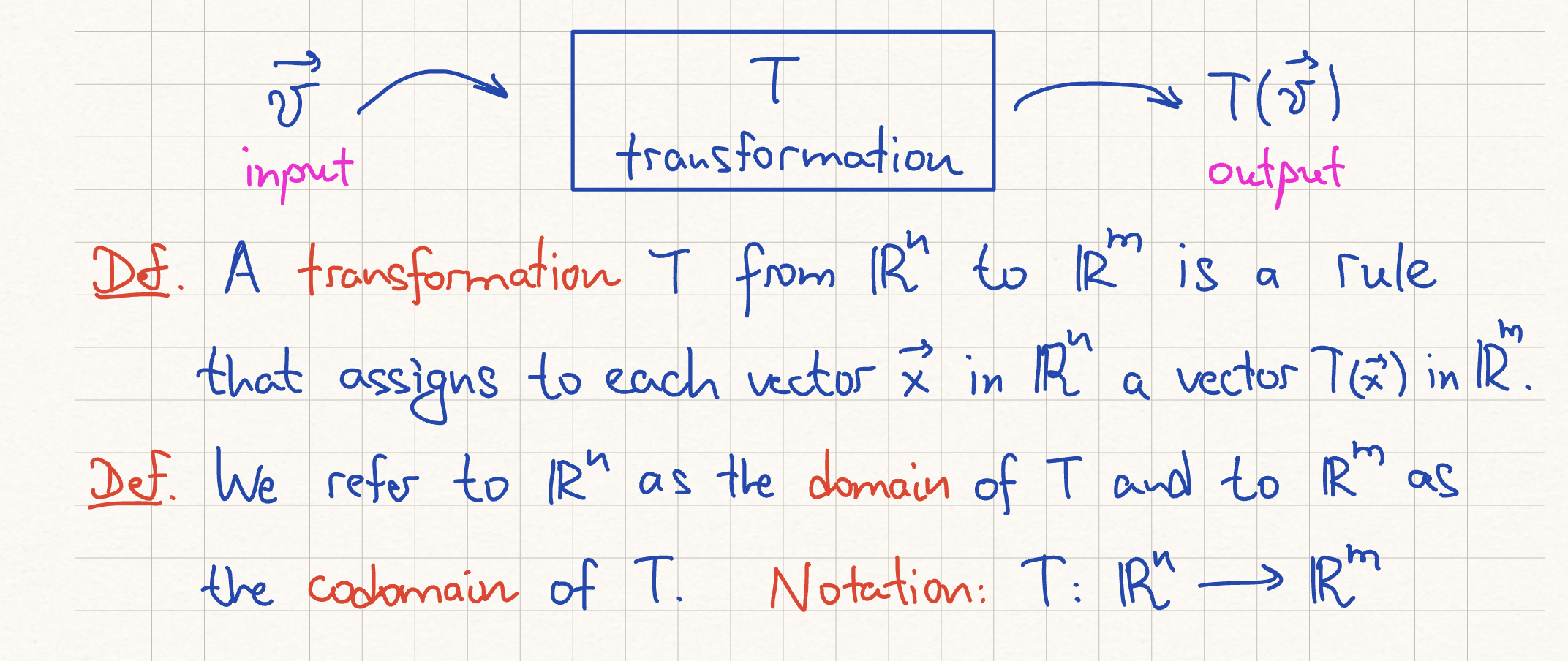
image, range of transformation

Linear Transformation Conditions

Linear Transformation Properties

matrix transformations and linear transformations

Every linear transformation is a matrix transformation and vice versa

superposition principle

The superposition principle in physics is a direct application of the properties of linear transformations. It states that the net response at a given place and time caused by two or more stimuli is the sum of the responses that would have been caused by each stimulus individually. just the conditinos applied

Computing Matrix of Linear Transformation Theorem

Onto Transformation Theorem

One-to-One Transformation Theorem

(T/F) The columns of the standard matrix for a linear transformation from Rn to Rm are the images of the columns of the nxn identity matrix.

True (T). The columns of the standard matrix for a linear transformation from Rn to Rm are the images of the columns of the n×n identity matrix. As explained in problem 23, the standard matrix for a linear transformation T is constructed by applying the transformation to the standard basis vectors e1​,…,en​ and using the resulting vectors as the columns of the matrix. The j-th column of the standard matrix is the vector T(ej​).

names of theorems

know em

diagonal matrix

a_ij = 0 for all i =/= j

Properties of Matrix Arithmetic

Properties of Matrix Multiplication

Properties of Matrix Transpose

(T/F) Each column of AB is a linear combination of the columns of B using weights from the corresponding column of A. 

The correct rule of matrix multiplication is that each column of the product AB is a linear combination of the columns of A using weights from the corresponding column of B. The statement reverses the roles of matrices A and B.

Suppose the last column of AB is all zeros, but 𝐵 itself has no column of zeros. What can you say about the columns of 𝐴?

Let the last column of B be bk​. We are given that Abk​=0 and bk​=0. This means that the equation Ax=0 has a non-trivial solution, namely x=bk​. By the Invertible Matrix Theorem, if Ax=0 has a non-trivial solution, then the columns of A are linearly dependent.

is the inverse unique

Inverse is Unique Theorem: If an inverse of a matrix exists, it is unique.

Elementary Matrix Relationship

It turns out that applying an elementary row operation to an mxn matrix A is equivalent to multiplying A by a corresponding mxm elementary matrix from the left. Get that matrix by applying the row operation to I

Invertible if and only if row equivalent to In theorem

Invertibility of 2×2 Matrices Theorem

Invertible Unique Solution Theorem

Properties of Invertible Matrices

Elementary Matrices Invertible?

Invertible Matrices Theorem

h) the columns of A span Rn
i) the linear transformation T(x) = A(x) is onto Rn
j) there is an nxn matrix C such that CA.= I
k) there is an nxn matrix D such that AD = I. 
l) A^T is an invertible matrix. 

x2 = x3 + m

x3 is free

A(c(vec_x)) = c(A(vec_x))

t1...tk are parameters

Connection between Homogeneous and Non-Homogeneous Systems Equation

Suppose the equation A(vec_x) = vec_b is consistent for some given vec_b, and let vec_p be a solution. Then the solution set of A(vec_x) = vec_b is the set of all vectors of the form vec_w = vec_p + vec_vh, where vec_vh is any solution to the homogeneous equation A(vec_x) = vec_0.
Geometrically, the solution set of A(vec_x) = (vec_b) is the result of translation of the solution set A(vec_x) = vec_0 by a vector vec_p.

Parametric Form of a Solution Set

vec_p + t1(vec_v1)... + tk(vec_vk)
vec_p is a vector such that A(vec_p) = vec_b
vec_v1..., vec_vk are solutions to the associated homogeneous system A(vec_x) = 0.
t1...tk are parameters