4.1: The Concepts of Force and Mass

• Force - the push or pull required to change the state of motion of an object, as defined by Newton’s second law.

  • A push or pull have an equivalent affect

  • Vector quantity

  • SI unit: Newton (N)

• Contact forces arise from physical contact.

  • Action at a distance forces DO NOT REQUIRE CONTACT and include gravity and electrical forces.

The Newton

N=\dfrac{kg\cdot m}{s^{2}}

\dfrac{N}{kg} is equal to \dfrac{m}{s^{2}}

4.2: Newton’s First Law of Motion

First Law of Motion

• An object will continue in a state of rest, or in a state of motion at a constant speed along a straight line, unless compelled to change that state by a net force greater than zero.

• Not all objects in motion have forces acting on them.

• Net force: vector sum of all forces acting on an object.

  • If no net force acts on an object, the objects velocity can not change.

  • If no net force acts on an object, the object can not accelerate.

  • Vector quantity

• Inertia - The natural tendency of an object to remain at rest OR in motion at a constant speed along a straight line.

  • Mass = quantitative measure of inertia.

  • SI unit of inertia and mass is the KILOGRAM (kg)

• Mass - the quantitative measure of inertia. SI unit: kilogram (kg).

• An inertial reference frame (non-accelerating frames of reference) is one in which Newton’s Law of Inertia is valid (at rest or moving with constant velocity).

  • All accelerating reference frames are non-inertial.

4.3: Newton’s Second Law of Motion

• When a net external force acts on an object of mass m, the acceleration that results is directly proportional to the net force and has a magnitude that is inversely proportional to the mass. The direction of the acceleration is the same as the direction of the net force.

Acceleration is proportional to the net force

• To be proportional example - if you double one quantity, you get double the other.

• Doesn’t have to be doubled, but it must match the other.

Magnitude is inversely proportional to the mass

• To be inversely proportional example - if you double one quantity, you get half of the other. If you triple it, you get 1/3 the other, and so on.

Main Equation:

• \sum F=ma

  • \sum = the sum of

  • F = Force

  • m = mass

  • a = acceleration

• SI unit for force: Newton (N)

Other variation: \overrightarrow{a}=\dfrac{\Sigma F}{m}

Free Body Diagrams

• A free body diagram is a diagram that represents the object and the forces that act on it.

• The object is usually represented by a dot.

4.4: The Vector Nature of Newton’s Second Law of Motion

• The directions of vectors can be taken into account in two dimensions by using x and y components.

• x-axis equation: \sum F_{x}= ma_{x}

• y-axis equation: \sum F_{y}= ma_{y}

4.5: Newton’s Third Law of Motion

Third Law of Motion

• Whenever one body exerts a force on a second body, the second body exerts an oppositely directed force of equal magnitude on the first body.

• For every action (force) there is an equal, but opposite reaction.

• Even though the magnitude of the action and reaction forces are always equal these forces do not necessarily produce accelerations that have equal magnitude since each force acts on a different object that may have a different mass.

Weight of an Object

Always acts downwards

Equation: \ W=mg

W = Weight

m = mass

g = gravity

4.7: The Gravitational Force

Newton’s Law of Universal Gravitation

• Every particle in the universe exerts an attractive force on every other particle.

• For two particles, which have masses m₁ and m₂ and are separated by a distance r, the force that the particles, and has a magnitude given by:

  • F=G\dfrac{m_{1}m_{2}}{r^{2}}

  • F = Force (weight)

  • Universal gravitational constant: G = 6.67259× 10^-11 \dfrac{N\cdot m^{2}}{kg^{2}}

  • m = mass

  • r = distance

• What happens to the force if…

  • We double m₁: F=G\dfrac{((2)m_{1})m_{2}}{r^{2}}

    • The force of gravitational attraction will also double. This is because F is directly proportional to m₁.

  • We triple m₂: F=G\dfrac{m_{1}((3)m_{2})}{r^{2}}

    • The force of gravitational attraction will also triple. This is because F is directly proportional is directly proportional to m₂.

  • We double m₁ and triple m₂: F=G\dfrac{((2)m_{1})((3)m_{2})}{r^{2}}

    • The force of gravitational attraction will be a factor of 2×3=6 increase. This means the force will increase by a factor of 6.

  • We double r: F=G\dfrac{m_{1}m_{2}}{(2)r^{2}}

    • The gravitational force decreases to one-fourth of its original value.

• Inverse square law: The inverse square las states that a physical quantity decreases as the square of the distance ( r ) from a source increases.

Weight

• Weight - gravitational force that the earth (or other astronomical body) exerts on an object.

  • W=mg

  • Weight is a vector quantity.

  • Always acts downwards towards the center of the body.

  • SI unit of weight: newton (N)

• Mass of the Earth

  • Equation: W=G\dfrac{M_Em}{r^{2}}

• g is equal to G\dfrac{M_E}{r^{2}}

4.8: The Normal Force

Normal Force

• The normal force is the component of a contact force that is perpendicular to the surface that an object contacts (force that a surface exerts on an object).

• Magnitude of the normal force indicates how hard the two objects press against each other.

• If an object is resting on a surface, there are no vertical forces acting on them. The magnitudes of these two forces are equal.

Apparent Weight

• Apparent weight of an object is the reading of a scale.

• It is equal to the normal force the man exerts on the scale.

• \sum F_{y}=+F_{N}-mg=ma

• F_{N}=mg+ma

  • F_{N} = apparent weight

  • mg = true weight

• g can not be negative, a can be positive or negative.

4.9: Static and Kinetic Friction

• When objects move on surfaces, there is a parallel force to the surface which is called frictional force (aka friction).

The Direction of Friction

• Friction is ALWAYS the opposite direction of motion.

• Orientation does not matter (vector direction).

Static Friction

• Static friction - the frictional force resists force that is applied to an object, and the object remains at rest until the force of static friction is overcome.

  • f_{s}=\mu_s \cdot F_{N}

• Maximum static friction - the force just before breakaway (right before object starts moving).

  • f_{s}^{MAX}=\mu_s \cdot F_{N}

• Static friction opposes the impending relative motion between two objects

• \mu_s = coefficient of static friction.

Kinetic Friction

• Kinetic friction is a force that acted between moving surfaces.

• Kinetic frictional force opposes the relative sliding motion.

• Kinetic = moving

• f_{\text{k}} = \mu_k \cdot F_{N}

• 0\leq \mu _{k} is the coefficient of kinetic friction.

Three Main Characteristics of Kinetic Frictional Force

1. It is independent of the apparent area of contact between the surfaces

2. It is independent of the speed of the sliding motion, if the speed is small.

3. The magnitude of the kinetic frictional force is proportional to the magnitude of the normal force.

4.10: The Tension Force

• Cables and ropes transmit forces through tension.

• Massless ropes transmit tension undiminished from one end to the other.

• Frictionless pulleys transmit tension to the other end of the rope undiminished.

• T = Tension

Pulleys:

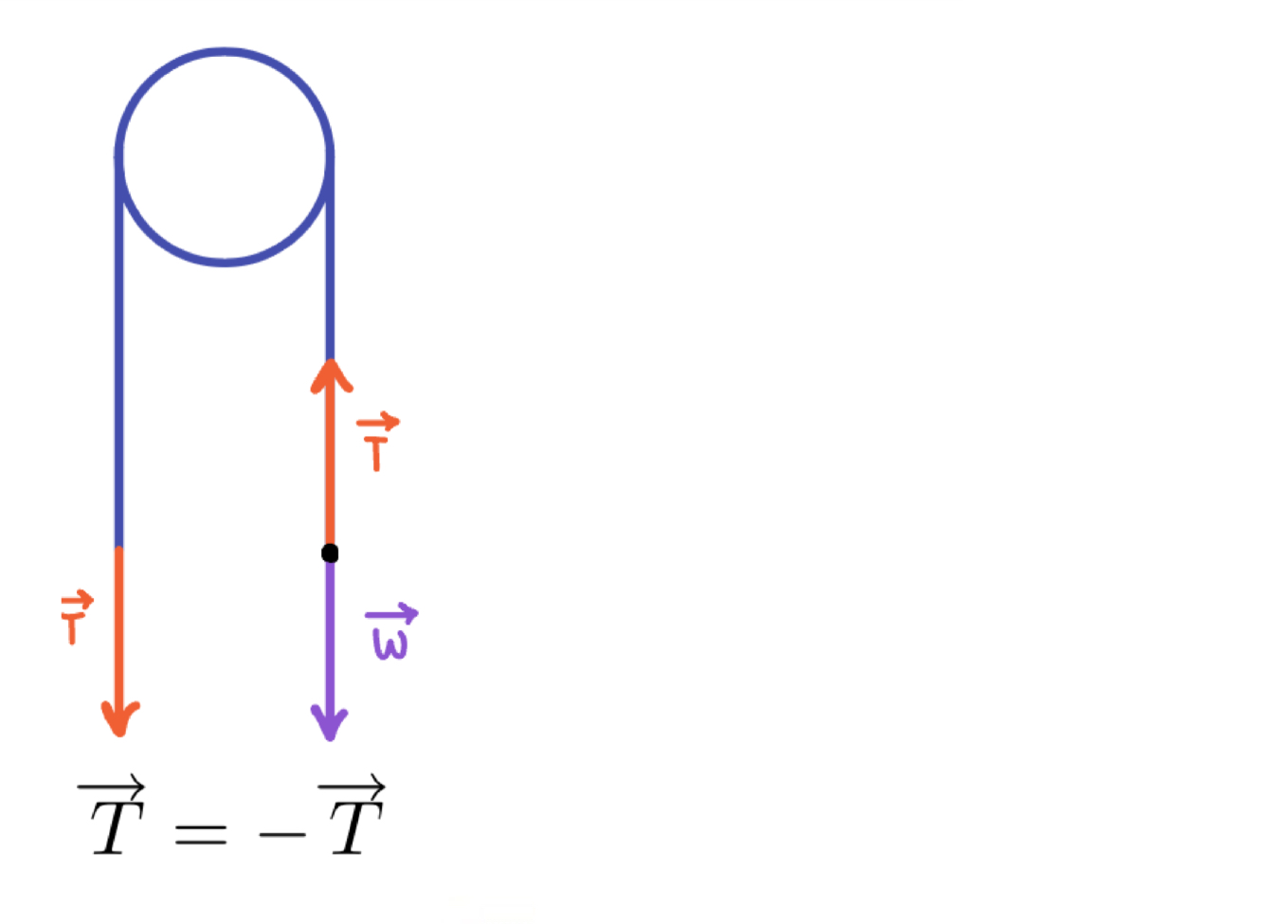Hanging objects:

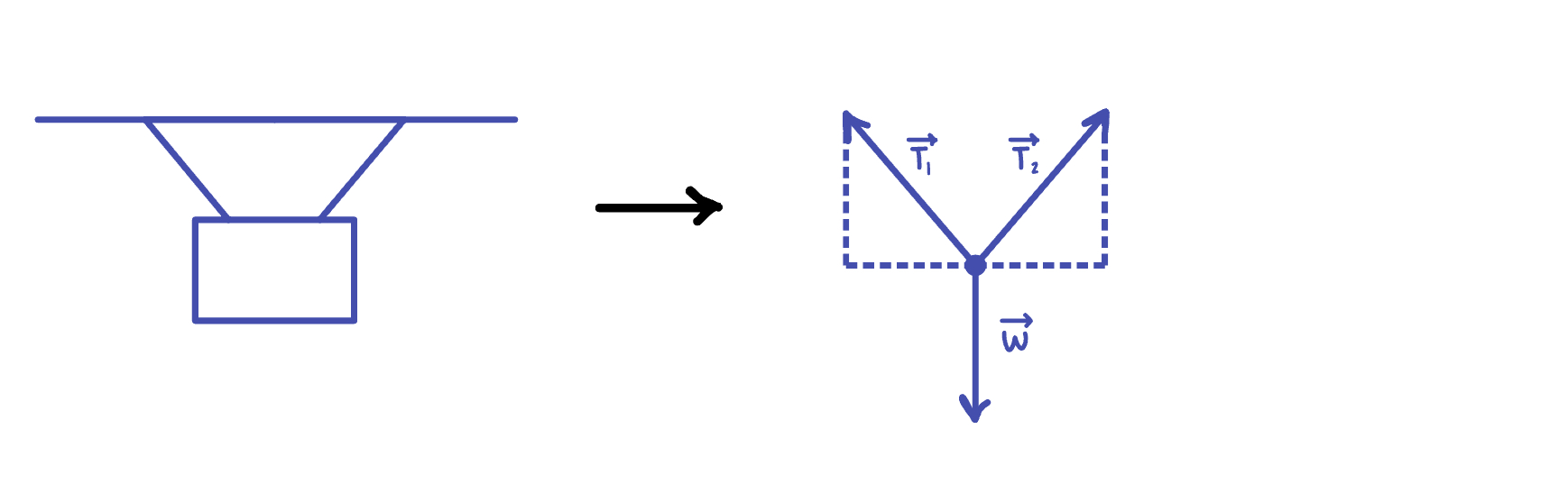
4.11: Equilibrium Application of Newton’s Laws of Motion

• Equilibrium refers to lack of change in the velocity of an object (the object is not accelerating).

• An object is in equilibrium when it has ZERO ACCELERATION.

  • \sum F_{x}=0

  • \sum F_{y}=0

• When an object is accelerating, it is NOT in equilibrium.

  • \sum F_{x}=ma_{x}

  • \sum F_{y}=ma_{y}

• Newton’s laws apply to objects whether or not they are in equilibrium.

• The forces acting on an object in equilibrium must balance.

• An object can be moving and still be in equilibrium if there is no acceleration.

Equilibrium Problems

• When \sum F=0 , a system is said to be at equilibrium, so, because acceleration is zero, itsvelocity will NOT change.

• It will keep doing whatever it is doing (stay at rest or stay in motion).

Non-Equilibrium Problems

• When \Sigma F\neq 0 , the net F will make the system accelerate, so its velocity WILL change.

• It will speed up, slow down, or stop.

Examples: Equilibrium or Non-Equilibrium

• Equilibrium

  • A car parked on the road.

  • A car moving north at a constant speed of 75 mph.

  • A plane climbing at a constant speed in a straight line.

  • An I-beam lowered down by a crane at constant speed.

• Non-Equilibrium

  • A car starting from a stop and moving straight through an intersection.

    • Accelerating.

  • A car making a right turn at constant speed.

    • There is a change in direction.

  • A skydiver in free fall just after stepping out of a plane.

  • A stunt motorcyclist at the peak of a jump over a fountain.

Overview: Fundamentals of Newton's Laws

Newton's First Law: Law of Inertia

• An object at rest will stay at rest, and an object in motion will stay in motion with a constant velocity unless acted upon by an external force.

• Inertia is the tendency of an object to resist changes in its motion.

• The net force acting on an object is zero when it is in equilibrium.

Newton's Second Law: Law of Acceleration

• The acceleration of an object is directly proportional to the net force acting on it and inversely proportional to its mass.

• The equation is F = ma, where F is the net force, m is the mass, and a is the acceleration.

• The direction of the acceleration is the same as the direction of the net force.

Newton's Third Law: Law of Action-Reaction

• For every action, there is an equal and opposite reaction.

• When one object exerts a force on another object, the second object exerts an equal and opposite force on the first object.

• The forces always act on different objects and are simultaneous.

Applications of Newton's Laws

• Newton's laws are applicable to both stationary and moving objects.

• They are used to explain the motion of objects on Earth and in space.

• They are fundamental in understanding concepts like force, mass, acceleration, and equilibrium.

• These laws are the basis for many engineering and scientific calculations.

Limitations of Newton's Laws

• Newton's laws are valid only in an inertial frame of reference.

• They do not apply to objects moving at speeds close to the speed of light or in extreme gravitational fields.

• At the atomic and subatomic level, quantum mechanics takes precedence over classical mechanics.

Conclusion

• Newton's laws provide a foundation for understanding the behavior of objects in motion.

• They describe the relationship between forces, mass, and acceleration.

• These laws have widespread applications in various fields of science and engineering.